A k-means nonlinear manifold clustering and representative point selecting method based on a graph theory

A nonlinear manifold and representative point technology, applied in the field of k-means nonlinear manifold clustering and representative point selection, can solve problems such as unfavorable large-scale application and complex optimization process

Active Publication Date: 2014-03-05
SHANGHAI JIAO TONG UNIV
View PDF3 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Other nonlinear manifold clustering methods either require harsh preconditions (for example, only valid for analytical manifolds or require good s

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A k-means nonlinear manifold clustering and representative point selecting method based on a graph theory
  • A k-means nonlinear manifold clustering and representative point selecting method based on a graph theory
  • A k-means nonlinear manifold clustering and representative point selecting method based on a graph theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0040] Example 1: Manifold Clustering Case

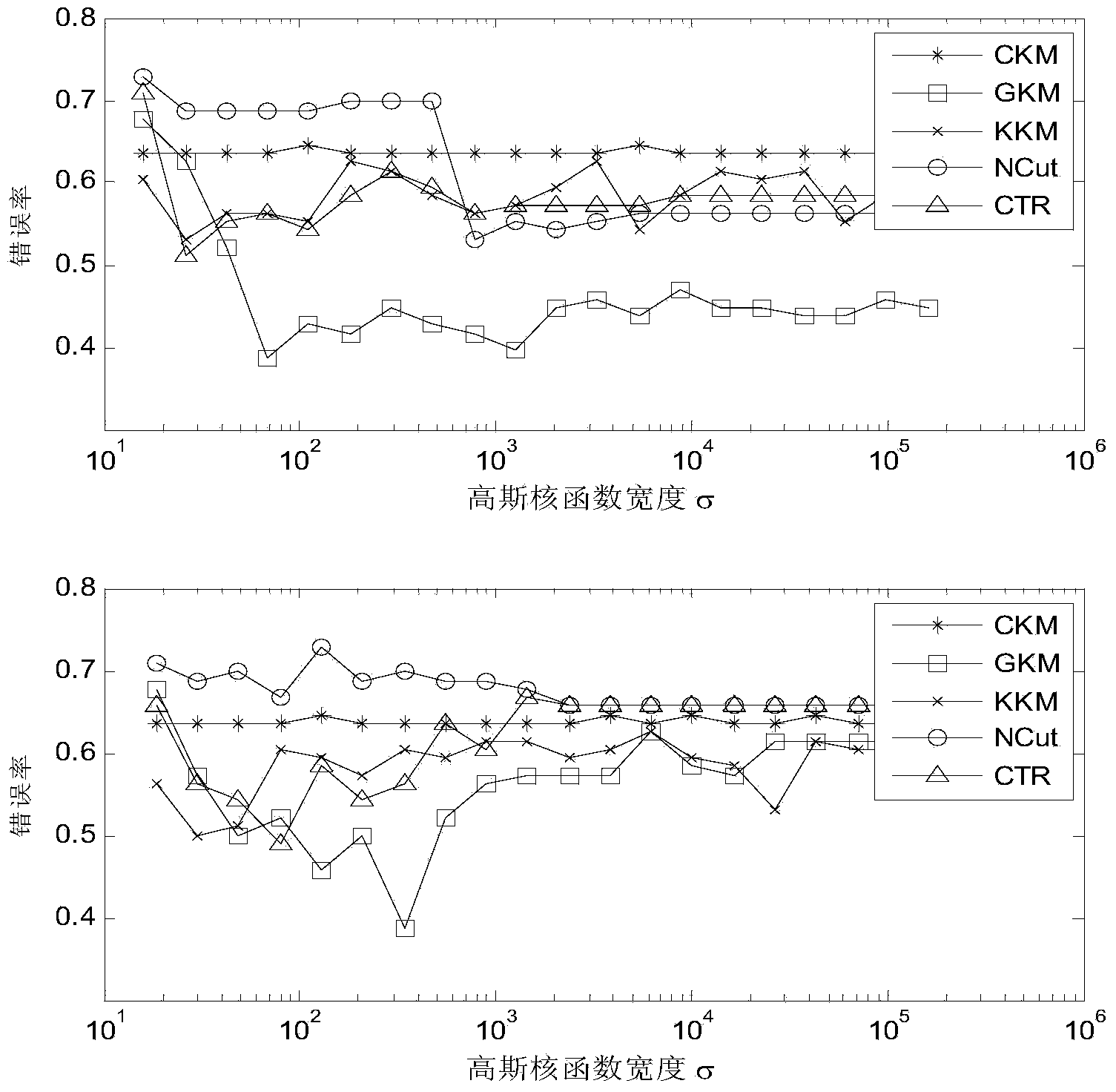
[0041] In this embodiment, face images are clustered, and four groups of different face photos are selected, and each group includes 24 face photos of the same person, and each photo is taken under different angles, illumination and expressions, and finally each The size of the photos is normalized to 64×64, and then each image is arranged column by column into a 4096-dimensional column vector. A total of 96 face image vectors constitute a face dataset (hereinafter referred to as the dataset). First, use all the photos to construct a kNN graph (in order to reflect the reliability of the results more comprehensively, here k takes two values ​​of 5 and 10 to operate once respectively). The specific implementation process is as follows:

[0042] 1. Build a kNN graph. Each vector in the data set is used as a node of the graph, and the adjacent nodes are defined as follows: according to the Euclidean distance, each node is connected to...

Embodiment 2

[0052] Example 2: A case of representative point selection

[0053] In order to verify the performance of the present invention in the selection of representative points, this embodiment is tested on 2 artificially synthesized data sets and 4 actual data sets. According to the given number of representative points K, the specific implementation process is as follows:

[0054] 1. Build a kNN graph. Each vector in the data set is used as a node of the graph, and the adjacent nodes are defined as follows: according to the Euclidean distance, each node is connected to the k nodes closest to it in the data set;

[0055] 2. Calculate the graph matrix and graph distance matrix. The calculation method of the adjacency matrix W of the graph is as follows: if the i-th node is adjacent to the j-th node, the (i, j)th element of W is set Where σ is the Gaussian kernel function parameter, which varies from dataset to dataset; if the i-th node is not adjacent to the j-th node, the (i,j)t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention provides a k-means nonlinear manifold clustering and representative point selecting method based on a graph theory. Specifically, the method comprises following steps: constructing a graph model; calculating a graph distance matrix and an infinite random walk probability matrix between various sample points; and alternately iterating various clustering centers and clustering members on the graph model until convergence. A fatigue random walk model provided in the invention may fast achieve nonlinear manifold clustering and select a representative point for each cluster so as to overcome a defect that conventional k-means just achieves a good effect when samples comply with Gaussian distribution. The method has a good clustering effect on high-dimensional data with lower-dimensional manifold distribution, such as images, texts, and videos, and may assign a most representative point to each cluster. The method is easy to implement and manipulate.

Description

technical field [0001] The invention relates to the technical field of sample clustering in machine learning and pattern recognition, in particular to a graph theory-based k-means nonlinear manifold clustering and representative point selection method. Background technique [0002] Modern scientific research shows that many high-dimensional data obey the manifold distribution, and the manifold dimension of the data distribution is generally much lower than the dimension of the data itself. For example, a 100x100 face image has 10,000 data dimensions, and in the process of face recognition, for different face photos of the same person, there may only be dozens or even several key factors that play a decisive role, such as facial features The size, proportion, face shape and expression of each person, and these key factors of each person are subject to a certain distribution, that is, the low-dimensional manifold distribution. How to fully exploit these internal factors to im...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06T7/00
Inventor 屠恩美杨杰
Owner SHANGHAI JIAO TONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap