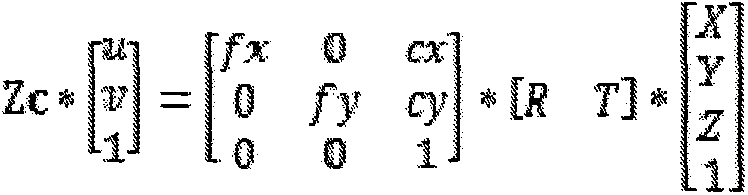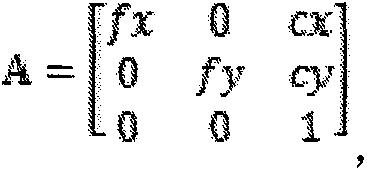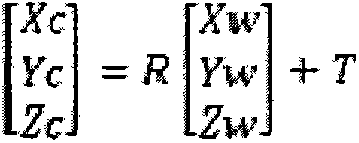Supercharge Your Innovation With Domain-Expert AI Agents!

Water flowing speed monitoring method based on moving target identification in videos

A moving target, speed monitoring technology, applied in the direction of fluid velocity measurement, velocity/acceleration/impact measurement, measurement device, etc., can solve the problems of low safety, high risk factor of ship measurement method and high cost

Inactive Publication Date: 2014-09-10
嘉兴博海信息科技有限公司 +1
View PDF0 Cites 27 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these traditional methods often have some important defects
Although the Acoustic Doppler Velocity Measurement method has high precision, it has high cost and low safety, especially during the high flood period, the ship measurement method has a high risk factor; , if the water level of the flood does not exceed the normal layout position, the measurement results will be unreliable

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Water flowing speed monitoring method based on moving target identification in videos
  • Water flowing speed monitoring method based on moving target identification in videos
  • Water flowing speed monitoring method based on moving target identification in videos

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0029] The present invention will be described in detail below in conjunction with the examples. This technology uses video monitoring technology to form a sequence of images in real time on the flow of the river section, automatically detects and tracks the buoys on the water surface in the sequence images, and uses the principles of solid geometry and photogrammetry to establish a conversion model between the image and the actual water surface coordinates to obtain the buoyancy The time and moving distance of objects moving in the field of view are calculated to obtain the flow velocity of the flood. Place suspended objects as buoys in the river, select the field of view of the camera, and place the camera fixedly for recording. The reality of the present invention mainly includes the following aspects: video-based moving target detection and tracking, camera calibration method and the parameters obtained through the previous steps to solve the water velocity.

[0030] 1. V...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a water flowing speed monitoring method based on moving target identification in videos. According to the method, steps of moving target detection and tracking based on the videos, camera calibration and water flowing speed solving are adopted for measuring the flowing speed of flood. The water flowing speed monitoring method is characterized in that the participation of work personnel is reduced so that the equipment is simple, and the test duration is short; meanwhile, the safety is greatly improved; in addition, the missing detection of flood peaks is enabled to be avoided; thus the automation degree is higher; the cost is reduced; and the actual applicability is high.

Description

technical field [0001] The invention relates to a water speed monitoring system, in particular to a water speed monitoring system based on moving target recognition in video. Background technique [0002] The flow velocity measurement methods that are often used in practical applications are as follows: the method of measuring flow velocity by using the acoustic Doppler principle, as well as some current velocity meter methods, gradient-area methods and traditional The three methods of measuring flow velocity are the buoy method. But these traditional methods often have some important defects. Although the acoustic Doppler velocity measurement method has high precision, it has high cost and low safety, especially during the high flood period, the ship measurement method has a high risk factor; , if the water level of the flood does not exceed the normal layout position, the measurement results will be unreliable. The flow velocity measurement method based on moving target...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06T7/20G01P5/18
Inventor 李荣龚建华李毅
Owner 嘉兴博海信息科技有限公司
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com