Method for obtaining electric power system node impedance matrix through LDU triangular decomposition based on symmetrical sparse matrix technology
A technology of node impedance matrix and triangular decomposition, which is applied in the direction of complex mathematical operations, etc., can solve the problem of slow calculation speed, inability to use L and U factor matrix element symmetry, sparsity and their relationship, and unsatisfactory calculation results, etc. question
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
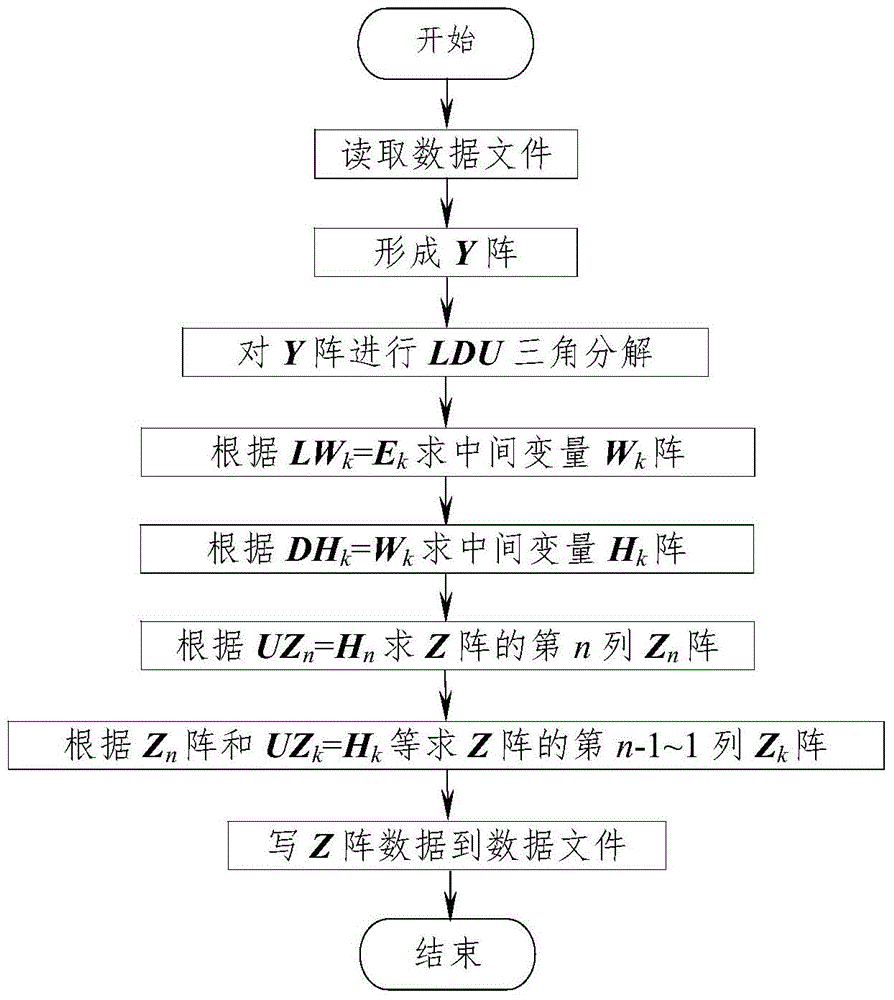
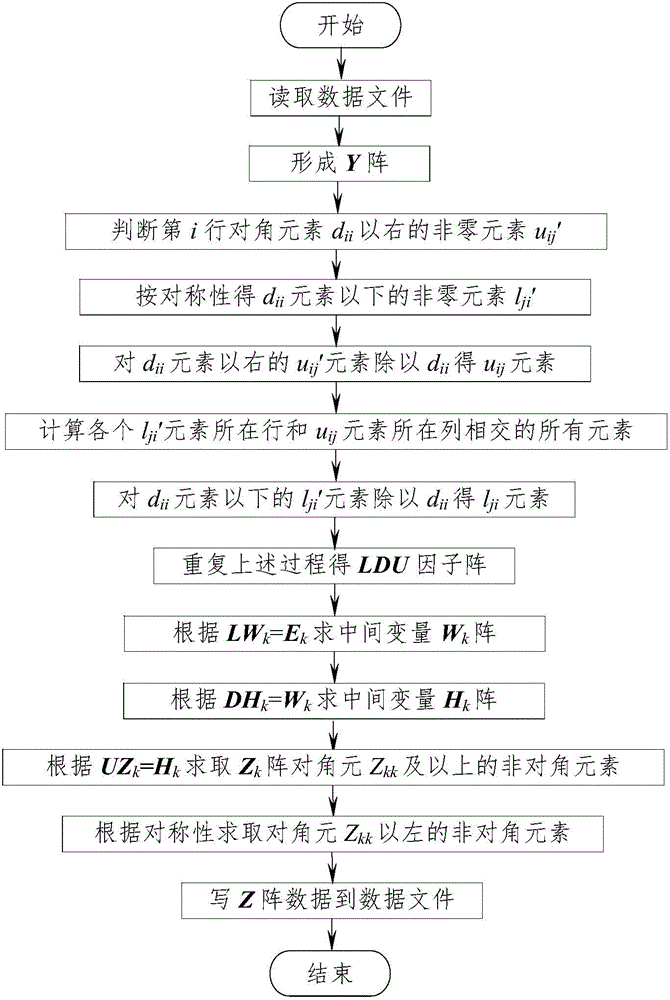
[0032] The traditional LDU triangular decomposition method ( figure 1 ) and the inventive method ( figure 2 ) Find the elements of the Z matrix for the Y matrix of the IEEE-30, -57, -118 node systems, and compare the average calculation time of the "decomposition" and "decomposition + back-substitution" processes. The calculation results are shown in Table 1.
[0033] Table 1 The influence of sparsity and symmetry on the process time of "decomposition" and "decomposition + back substitution" of LDU triangular decomposition method
[0034]
[0035] T 1 : The average calculation time of the traditional LDU triangular decomposition method in the "decomposition" process
[0036] T 2 : The average calculation time of the inventive method in the "decomposition" process
[0037] T 11 : The average calculation time of the traditional LDU triangular decomposition method in the process of "decomposition + back substitution"
[0038] T 21 : the average calculation time of the...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com