[0025] Examples:
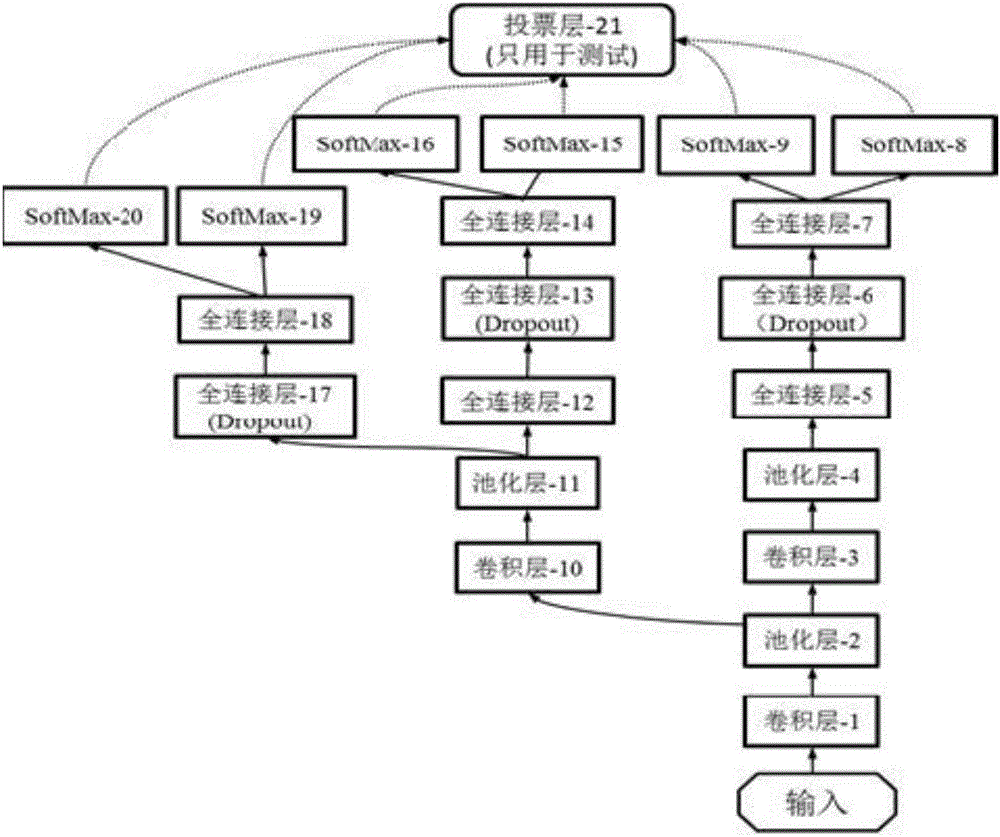
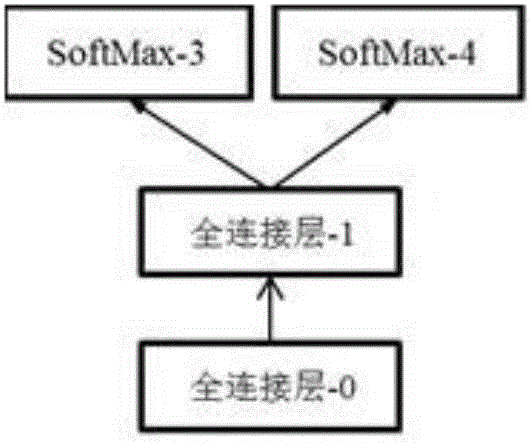
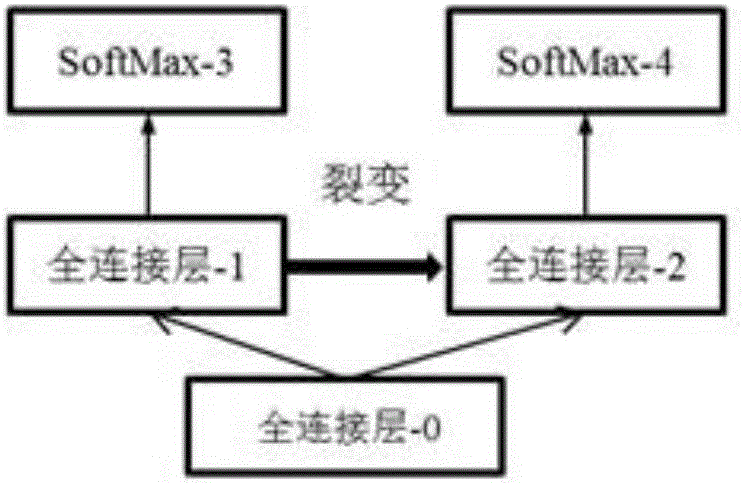
[0026] We propose a new deep neural network structure named "Fissile Deep Neural Network". The network structure includes multiple branches with shared parameters and multiple Softmax classifiers; and during training, the structure of the entire network changes dynamically until the entire network structure is split into multiple models.
[0027] The fissionable deep neural network structure is a tree structure with shared parameters, such as figure 1 As shown, the entire structure includes an input layer, a convolutional layer, a pooling layer, a fully connected layer, a SoftMax layer, and a voting layer. The connection between each layer is carried out through data transfer. The root node is the data input layer, and all the leaf nodes are the Softmax layer. The voting layer is only used during testing. The numbers following the names of each layer are just to better distinguish each layer and have no other meaning. The path from the root node to a certain leaf node is a neural network with a linear structure.
[0028] In the tree structure, nodes with multiple outputs are called splittable nodes. E.g figure 2 The shown sub-network structure node is fully connected to layer-1. During training, when SoftMax-3 or SoftMax-4 converges to a very poor local optimal solution, the fully connected layer-1 begins to split, such as image 3 Shown. Fully connected layer-2 is fissioned from fully connected layer-1, and its parent node and child node are inherited from fully connected layer-1 node. The parameters of fully connected layer-2 are different from those of fully connected layer-1, and are initialized independently.
[0029] The purpose of fission is also to avoid convergence interference, such as figure 1 As shown, multiple branches share most of the parameters, because there are multiple Softmax layers, which involves the optimization of multiple object functions. However, neural networks can effectively solve the problem of non-convex function optimization. During training, each branch makes nodes that share parameters quickly converge, and the features extracted by these nodes are transmitted forward to those nodes that are not shared. The difference in each branch is reflected by those non-shared nodes. This also ensures that we obtain different features through different feature detectors. After further training, each object function tries to find the best gradient descent direction, so the later shared node update parameters will interfere with different branches, so our proposed fissionable deep neural network can avoid interference in subsequent training .
[0030] Training method:
[0031] Each iteration of fissionable neural network training is from the input layer to the SoftMax layer, first the forward transmission, and then the backward transmission to the parameter update. The training method is depth-first search. When the iteration reaches a leaf node, all the nodes it passes through participate in forward conduction, reverse conduction and update parameters. Then another branch iteration is performed, so that the nodes that share the parameters are updated again, and the convergence is faster. Such as figure 1 In the structure shown, after six iterations, all the branch nodes are traversed once, and we also call these six iterations a covering iteration. Such as Figure 4 As shown, the number of times that the nodes of the fissionable deep neural network structure are traversed in one coverage iteration is different. Obviously, the number of traversals for each node n is equal to the number of leaf nodes corresponding to the node. So the learning rate of each node is 1/n times the original learning rate.
[0032] Fission mechanism:
[0033] Fission begins when the convergence rate of a branch decreases. If the smallest cost function value among multiple branches does not change in N epochs (all data sets after training are called an epoch), the splittable node will undergo fission before proceeding to the next epoch. The value of N can be determined by using a valid verification set or simply set to 10. Such an approach can be considered universally applicable to most fissionable network structures. N is a variable that controls the degree of convergence interference in subsequent training. With the increase of N, the layer of shared parameters will converge faster, but when N is large, the interference of different branches in subsequent training is very serious, and the convergence of the guide becomes slower. The value of N is set accordingly according to the complexity of the data set and network structure.
[0034] The algorithm for finding fissionable nodes is the lowest common ancestor algorithm, such as Figure 5 As shown, every N epochs, the leaf node with the worst convergence is selected, and then backtracking to find the first node with multiple children as the splittable node.
[0035] Ways to predict results:
[0036] Design a voting layer to predict the result. The number of times each test sample is tested is equal to the number of leaf nodes. The voting layer averages the prediction results of all branches.
[0037] y i = 1 N X j N y j i
[0038] N represents the number of branches, y i Is the probability of sample i, Is the probability of sample i of the jth branch.
[0039] To prove that our proposed fissionable deep neural network can improve the performance of the neural network, the experiment uses two general data sets, MNIST and CIFAR-10, for verification and evaluation. When designing the network, make every branch as different as possible. The Dropout method is used on each branch, and has been marked in the experimental structure diagram. Before training, we manually set the learning rate and initialize the parameters appropriately. In the experiment, the ReLU activation function is used after the convolutional layer and the fully connected layer. The whole experiment uses mini-batch stochastic gradient descent with a momentum value of 0.9 without using data augmentation. In response to the complexity of the data set, we have set up different fission mechanisms.
[0040] MNIST:
[0041] Our first experiment was conducted on this data set. The network structure used in the experiment is as follows figure 1 As shown, the root node takes the pixels of the image as input, and there are 6 Softmax layers on the branch. From the root node to a leaf node, we call it a model. As shown in Table 1, the structure has six models. We call them model-1, model-2, model-3, model-4, model-5, and model-6. This experiment does not use data augmentation.
[0042] Our fission mechanism is as follows: during training, the first 40 epochs do not fission, which mainly allows different branches to share more parameters and accelerate convergence. Then every 10 epochs, the branch with the worst value of the function is selected for fission.
[0043] According to the above fission strategy mechanism, the error rate we obtained for this dataset is 0.43%, which is improved by 0.10%, 0.10%, 0.22%, 0.22%, 0.08%, 0.08% compared with the results of the other six models trained separately. It proves once again that the combination of multiple models can improve the performance of neural networks. The comparison of the eight methods is shown in Table 1 below.
[0044] Table 1. Comparison of test error rates of eight methods
[0045]
[0046] As shown in Table 1, the method F2_NoFission is based on figure 2 The structure of F2_Fission is trained, but the training process does not perform fission, but F2_Fission is trained according to the above-mentioned fission method. From Image 6 The comparison of these two methods can lead to a conclusion: the introduction of fission error rate in training reduces 0.05%. The improvement is not particularly obvious, mainly because the MNIST data set is too simple, and the error rate is already very low.
[0047] CIFAR-10:
[0048] For this data set, we designed the network structure and figure 2 Are very different, such as Figure 7 As shown, the structure has 5 Softmax classifiers, all the classifiers share all the parameters, we added the NIN technology, and the Dropout method is also applied behind the pooling layer. For this data set, we also did not use data augmentation.
[0049] The strategy for training the fission of this data set is as follows: in the first 15 epochs, each epoch is fissioned once, which is mainly to obtain multiple different branches at the beginning. Then there will be no fission between the 16th and 60th epochs, which is mainly to make different branches converge faster when sharing more parameters, and then after the 60th epoch, fission occurs every 10 epochs.
[0050] In this way, we have obtained an error rate of 13%, which is a reduction of more than 3% compared to F6_NoFission. The comparison of the two methods is shown in Table 2. The error rate of these two methods in the first 1000 epochs is as follows Picture 8 Shown.
[0051] Table 2. Comparison of error rates of the two methods in CIFAR-10
[0052]
