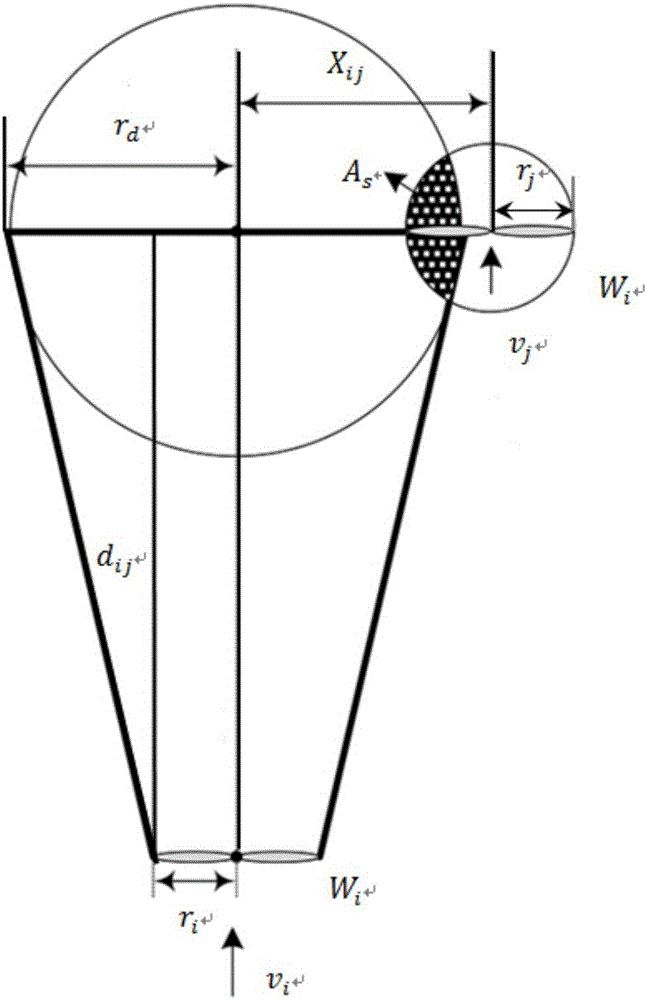
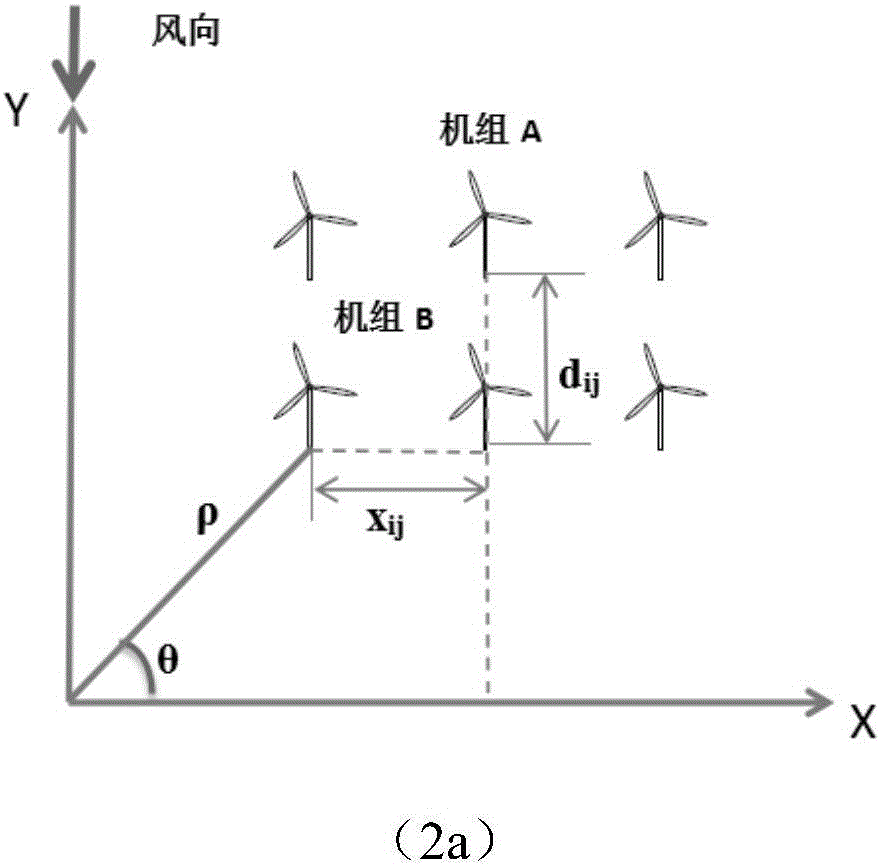
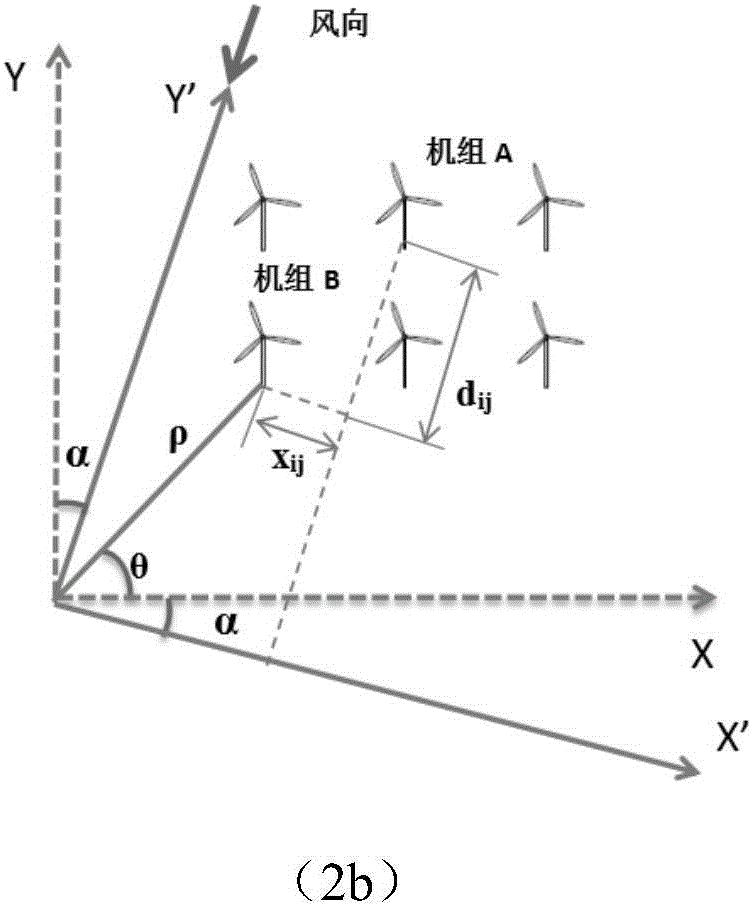
Optimization method for model selection of fan blade of wind power plant

A technology of fan blades and optimization methods, which is applied in the field of wind power generation, can solve problems such as the selection and optimization of the length of fan blades, and achieve the effects of simplifying the calculation of wake flow in multiple wind directions, reducing the cost of electricity, and improving efficiency

Inactive Publication Date: 2017-03-15
SHANGHAI UNIVERSITY OF ELECTRIC POWER +1
View PDF6 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the above studies are all carried out on the basis that the fans in the wind farm belong to the same model and the blade length is the same, and there are few studies on the selection and optimization of the blade length of the wind farm fan.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimization method for model selection of fan blade of wind power plant
  • Optimization method for model selection of fan blade of wind power plant
  • Optimization method for model selection of fan blade of wind power plant

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0047]The present invention will be described in detail below in conjunction with the accompanying drawings and specific embodiments. This embodiment is carried out on the premise of the technical solution of the present invention, and detailed implementation and specific operation process are given, but the protection scope of the present invention is not limited to the following embodiments.

[0048] This embodiment provides a wind farm fan blade selection optimization method, including the following steps: 1) obtain the capacity of the wind farm unit, and obtain the optional wind turbine type and the corresponding wind turbine blade length according to the capacity; 2) use the wind farm The goal is to minimize the cost of electricity in the whole life cycle, and the discrete wind turbine blade length is used as a constraint to establish an objective function; 3) The objective function is solved by a genetic algorithm to obtain the optimal combination of wind turbine types. ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention relates to an optimization method for model selection of a fan blade of a wind power plant. The method comprises the following steps: 1) acquiring a unit capacity of the wind power plant and acquiring the model of the selectable wind turbine unit and the length of the corresponding wind turbine unit blade according to the capacity; 2) establishing a target function by taking the minimal cost per kilowatt / hour in the life cycle of the wind power plant as a target and the length of the discrete wind turbine unit blade as a constraint; and 3) solving the target function according to a genetic algorithm, thereby acquiring the optimal model combination of the wind turbine unit. Compared with the prior art, the method has the advantages that the wind speed distribution of the wind power plant, the wake effect between the wind direction distribution and the unit and the life cycle cost of the wind power plant are comprehensively considered, the cost per kilowatt / hour of the wind power plant can be reduced under the condition of same wind power plant capacity, and a basis is provided for the model selection of the fan blades of an onshore wind power plant and an offshore wind power plant.

Description

technical field [0001] The invention belongs to the technical field of wind power generation, and in particular relates to a type selection optimization method for fan blades of a wind farm. Background technique [0002] With the rapid development of wind power technology, wind power has become the third largest power source after thermal power and hydropower. By 2020, my country's wind power installed capacity is expected to reach 200GW. The rapid development of wind power technology and the fierce competition of resources make the cost of electricity become one of the important indicators for the development of wind power industry. [0003] The cost per unit of electricity depends on the total cost and the amount of electricity generated. The power generation of a wind farm is determined by the amount of energy absorbed by the wind turbine from the wind. Among them, the blades of the fan are the key components for the fan to convert wind energy. Under the same capacity c...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/50
CPCG06F30/20G06F2111/06
Inventor 黄玲玲汤华符杨刘阳张开华张智伟
Owner SHANGHAI UNIVERSITY OF ELECTRIC POWER
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap