Transport equation response matrix block diagonalization method based on symmetric group theory
A technology of response matrix and symmetric group, applied in the field of nuclear reactor core design and safety, to achieve the effect of simplifying the solution, reducing the computing memory, and reducing the number of
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0050] Below in conjunction with accompanying drawing and specific embodiment the present invention is described in further detail:
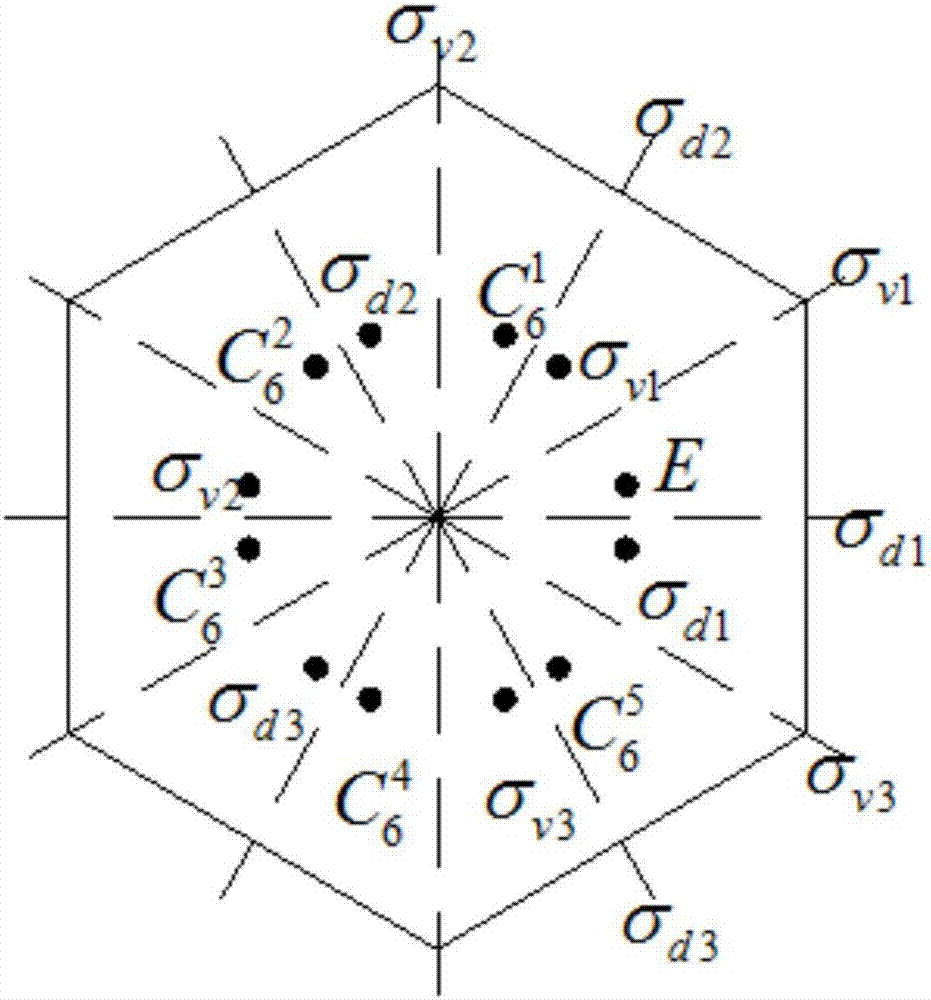
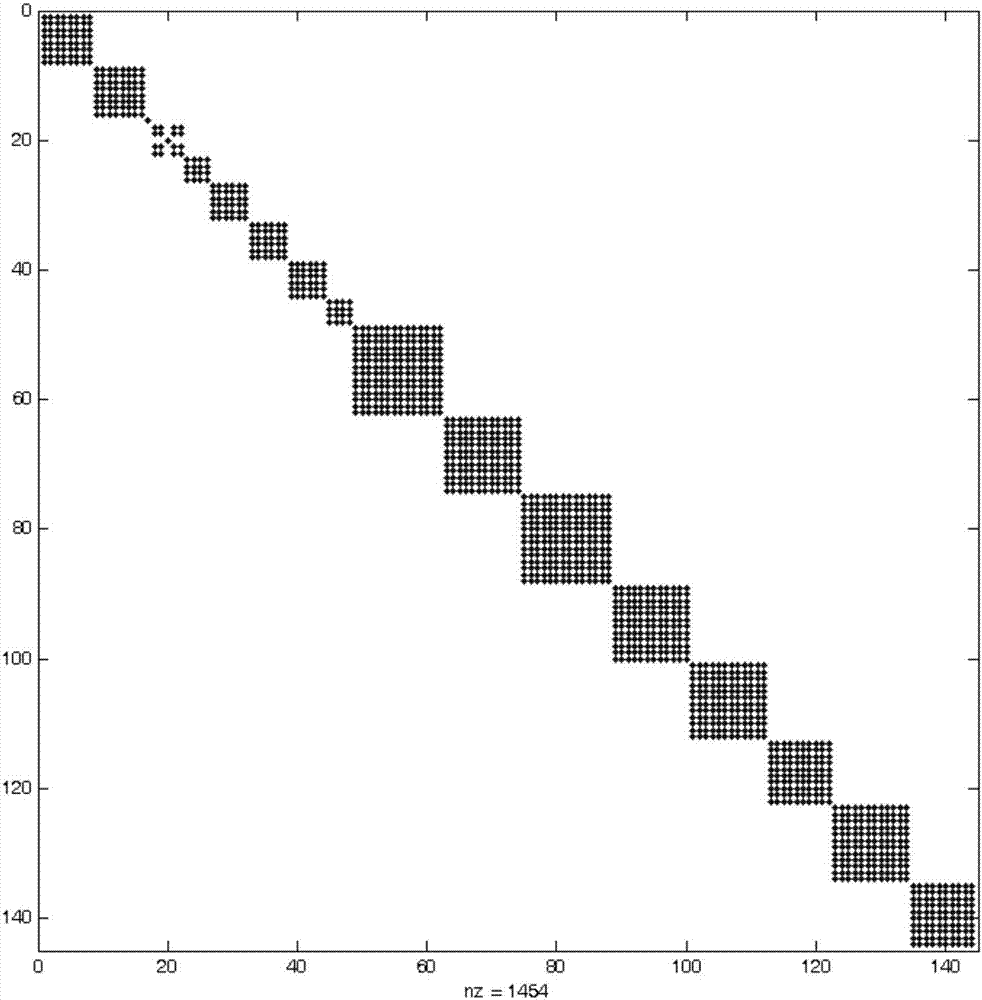
[0051] The method of the present invention will be based on the theory of symmetry groups, and adopt irreducible symmetrization basis functions to simplify the solution of the transport equation into several mutually decoupled sub-problems, thereby decomposing the response matrix into a series of mutually decoupled sub-problems located in the original matrix The subblocks at the diagonal positions of . In the matrix multiplication and inversion operations, the multiplication and inversion operations can be performed on the sub-block matrix independently, thereby greatly reducing the amount of floating-point operations of the matrix. In addition, due to the block-diagonalization of the matrix, the new matrix has significantly fewer non-zero elements compared to the original matrix, and the computational memory required to store the response matri...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com