Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for establishing constrained least square maximum entropy quantile function model

A least squares and function model technology, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve the problems of poor calculation accuracy and low calculation efficiency of the classical maximum entropy quantile value function model, and achieve calculation results. The effect of stable accuracy, high calculation efficiency and high calculation accuracy

Inactive Publication Date: 2017-09-08
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF0 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0008] Purpose of the invention: In view of the low calculation efficiency of the traditional probability statistics method and the poor calculation accuracy of the classic maximum entropy quantile function model in the case of small samples, the present invention proposes a method of constructing a constrained least square maximum entropy quantile function model method to improve the calculation efficiency and estimation accuracy of the quantile value function in the case of small samples

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for establishing constrained least square maximum entropy quantile function model
  • Method for establishing constrained least square maximum entropy quantile function model
  • Method for establishing constrained least square maximum entropy quantile function model

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0037] The present invention will be further described below in conjunction with the drawings and embodiments.

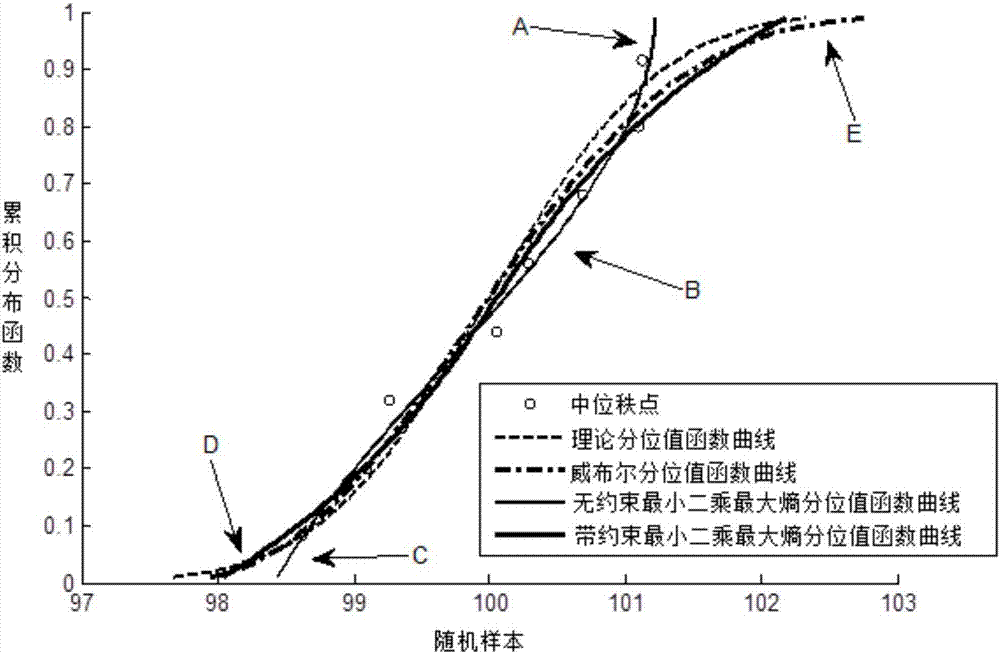
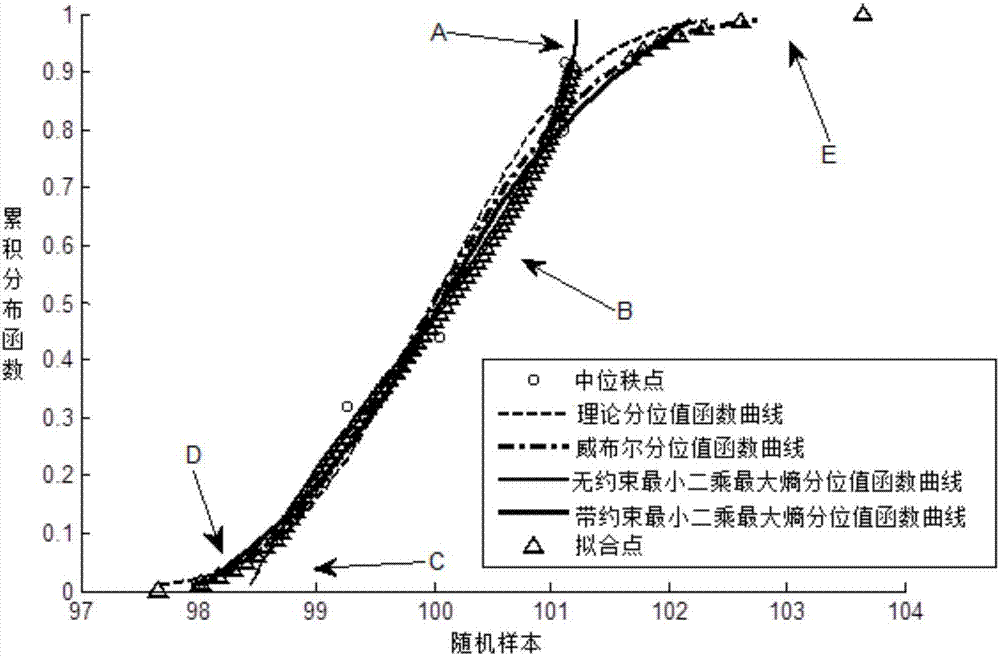
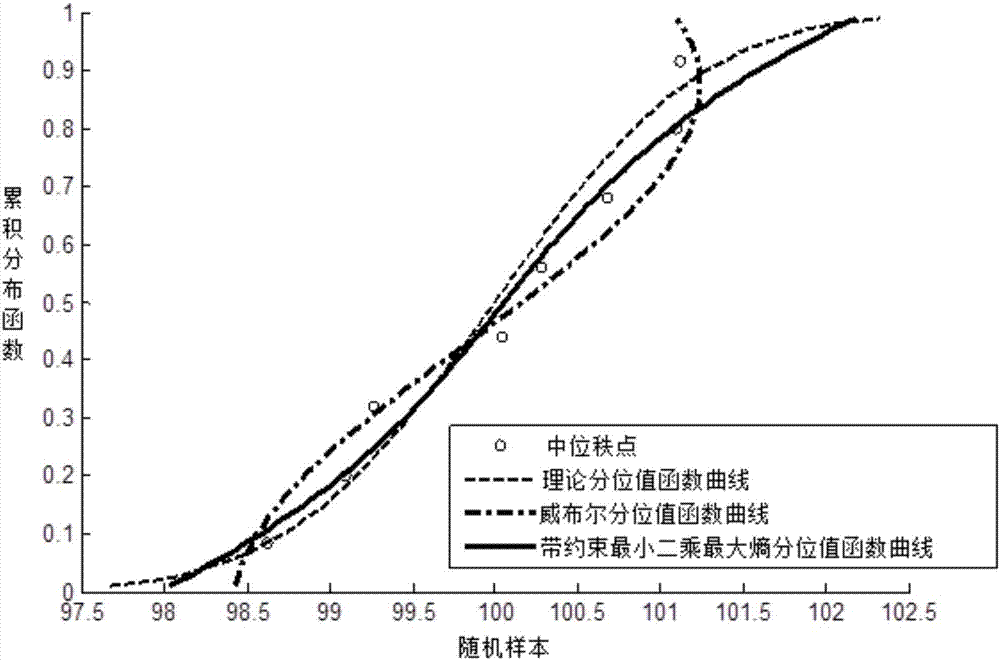
[0038] figure 2 Shown is the quantile function curve fitting process diagram based on the constrained least squares maximum entropy quantile function model, as follows:

[0039] 1) Establish an unconstrained least squares maximum entropy quantile function model

[0040] Set random variable X, u(x)=P(X≤x) is the cumulative distribution function value of X, and satisfy 0≤u(x)≤1, then the unconstrained least squares maximum entropy quantile function of random variable x(u) is:

[0041]

[0042] Where λ ls-qf, j (j=0,1,...,m) is the Lagrangian multiplier, that is, the undetermined coefficient; the number of Lagrangian multipliers is m+1. The cumulative distribution function u(x) and the unconstrained least squares maximum entropy quantile function x(u) are inverse functions to each other.

[0043] The steps to determine the Lagrange multiplier are as follows:

[0044] 11) Re-de...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a method for establishing a constrained least square maximum entropy quantile function model. The method comprises the steps of 1), establishing an unconstrained least square maximum entropy quantile function model; and 2), establishing a constrained maximum entropy quantile function model and method based on tail constraint of a Weibull distribution model the unconstrained least square maximum entropy quantile function model. The constrained least square maximum entropy quantile function model and method provided by the invention can be successfully applied to an aeronautic structure reliability analysis quantile function estimation problem under small sample condition. Compared with a traditional probability statistics method, the method has the advantages that high computing efficiency is achieved and complex random variables can be processed. Compared with a classic maximum entropy quantile function model, the method is high and stable in computing precision.

Description

[0001] Technical field: [0002] The invention relates to the field of reliability evaluation of aviation structural parts, in particular to a method for constructing a constrained least squares maximum entropy quantile function model in the reliability analysis of aviation structural parts in the case of small samples. [0003] Background technique: [0004] The external excitation based on aviation structural parts is not only related to the working conditions, but also affected by random factors, the inhomogeneity of material organization, the random distribution of internal defects, and the dispersion of dimensional tolerances during the manufacturing process. The reliability of the strength analysis process of aviation structural parts Analysis is a common problem: for example, in structural fatigue design, finding the fatigue life of a given reliability; in structural stiffness design, finding the structural displacement response of a given reliability, etc. [0005] At present, ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
CPCG06F30/15G06F30/17
Inventor 温卫东吴福仙翁晶萌陈波
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com