Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Right-angle cutting chatter analysis modeling method

A technology of right-angle cutting and modeling method, which can be used in measuring/indicating equipment, program control, instruments, etc., and can solve problems such as cumbersomeness and low accuracy of cutting force coefficients

Active Publication Date: 2017-09-12
WUHAN INSTITUTE OF TECHNOLOGY
View PDF6 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In view of the present situation of the above-mentioned prior art, the technical problem to be solved by the present invention is to provide a right-angle cutting chatter analytical modeling method, which can overcome the problem that the accuracy of the cutting force coefficient is too low and too cumbersome to be calibrated by experiments, and avoids the The cumbersomeness of the experimental calibration improves the accuracy of the cutting force coefficient and provides a more realistic prediction of cutting chatter stability

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Right-angle cutting chatter analysis modeling method
  • Right-angle cutting chatter analysis modeling method
  • Right-angle cutting chatter analysis modeling method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0058] The present invention will be further described in detail below in conjunction with the accompanying drawings and examples. The following examples are explanations of the present invention and the present invention is not limited to the following examples.

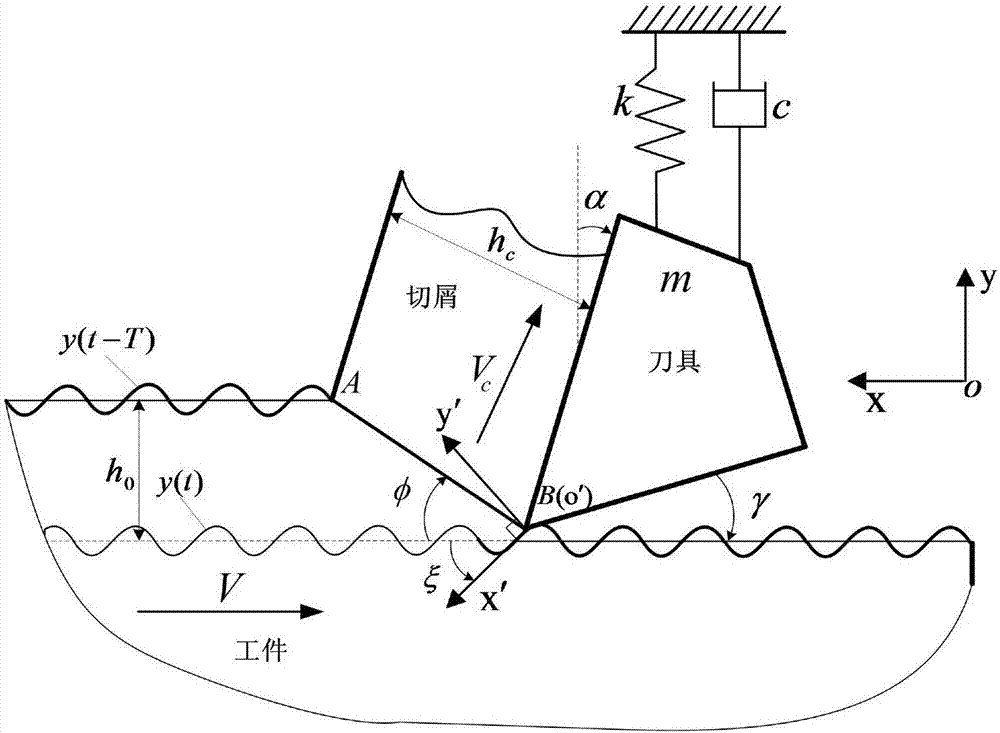
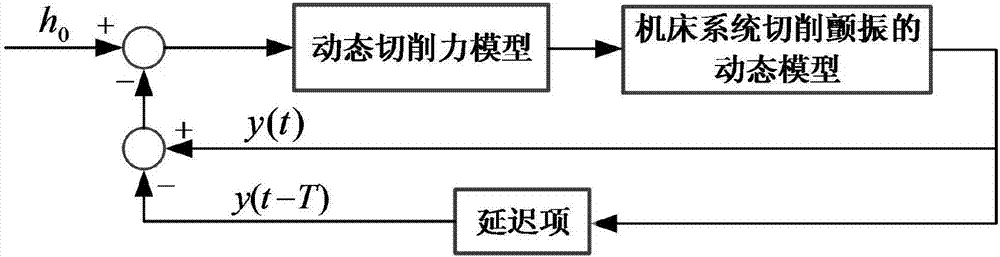
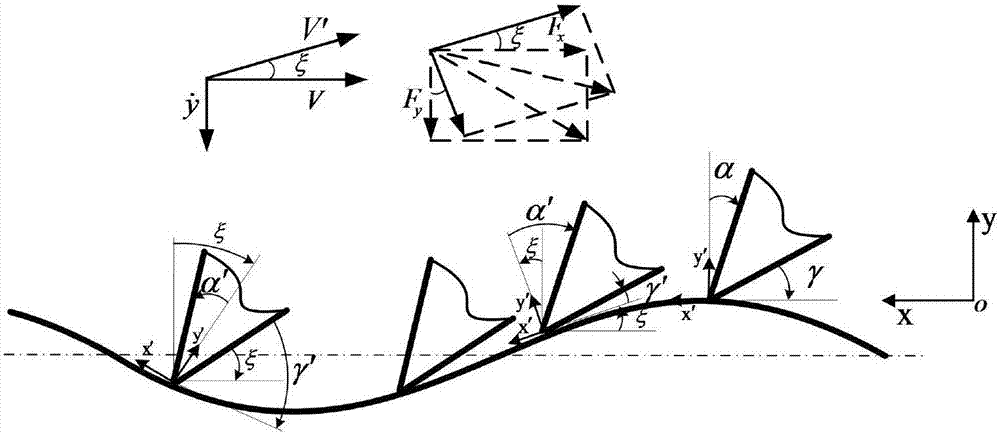
[0059] Such as Figure 1~3 As shown, a right-angle cutting chatter analytical modeling method, including the following steps:

[0060] Step 1, establish a dynamic model of chatter in right-angle cutting

[0061] Determine the geometric parameters of the tool, the rake angle α, the unit is deg, the relief angle γ, the unit is deg; select the cutting parameters, cutting speed V, the unit is m / min, the feed rate f t , the unit is mm / r, the cutting width b, the unit is mm; in the process of metal cutting, the change of cutting thickness will lead to the fluctuation of cutting force, the cutting force and cutting thickness change according to a specific cycle, and form a closed loop The feedback system calculates the d...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a right-angle cutting chatter analysis modeling method. The right-angle cutting chatter analysis modeling method comprises the following steps that firstly, a right-angle cutting chatter kinetic model is established; secondly, dynamic cutting force and a cutting force coefficient are calculated; and thirdly, a stability SLD figure of the right-angle cutting process is calculated. According to the right-angle cutting chatter analysis modeling method, the dynamic cutting process is regarded as the quasi-static cutting process at every moment, workpiece material features, tool geometry and cutting parameters are used as input parameters, the dynamic cutting force can be calculated through the cutting parameters which can be equivalently transformed, the expression of the dynamic cutting force coefficient is then theoretical deduced, through algebraic equation arrangement, the dynamic cutting force coefficient is obtained, the tediousness of experimental calibration is avoided, and the accuracy is improved; and in addition, the dynamic model of cutting chatter of a machine tool system can be expressed with a delay differential equation, the right-angle cutting chatter stability SLD figure is obtained with a time domain semi-discrete method through cutting stability analysis, and relatively real chatter stability prediction is provided.

Description

technical field [0001] The invention relates to the technical field of metal material cutting, in particular to a right-angle cutting chatter analytical modeling method. Background technique [0002] Cutting chatter is a chip regeneration phenomenon caused by the change of cutting force and the flexibility of the processing system, which is a form of self-excited vibration. When left unchecked, it can have a devastating effect on machined workpiece surface quality, material removal rate, surface dimensional accuracy, and tool and machine tool life. Therefore, establishing an effective chatter model is an effective measure to predict and avoid cutting chatter. [0003] So far, many machining chatter models have been formed, and there are mainly three methods used: analytical method, numerical method and experimental method, in which the cutting force coefficient is usually a constant determined by experimental methods. Obviously, obtaining reliable experimental data for a g...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): B23Q17/12
CPCB23Q17/12G05B19/4086
Inventor 付中涛陈绪兵戴耀南毛金城
Owner WUHAN INSTITUTE OF TECHNOLOGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com