Polynomial-based GF(2^n) multiplier
A technology based on polynomials and polynomials, which is applied to calculations using residual algorithms, calculations using non-numerical representations, etc., can solve the problems of multiplier size reduction and occupy a lot of space, so as to reduce complexity and space complexity The effect of reducing the overall volume
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0034] In order to make the object, technical solution and advantages of the present invention clearer, the specific implementation of the polynomial base GF(2^n) multiplier of the present invention will be described below in conjunction with the accompanying drawings. It should be understood that the specific embodiments described here are only used to explain the present invention, not to limit the present invention.
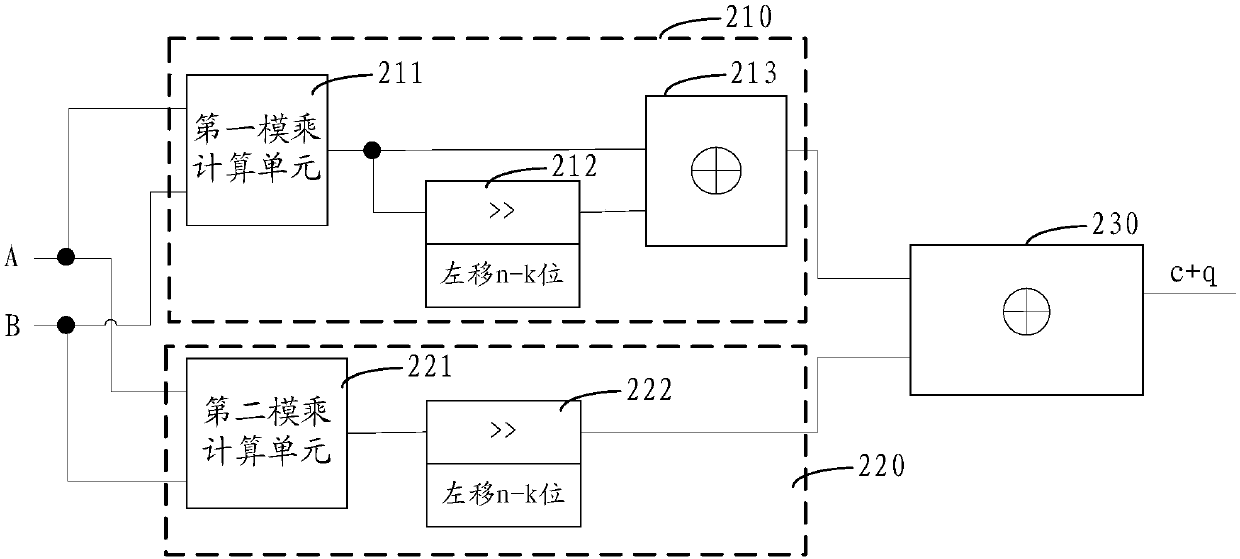
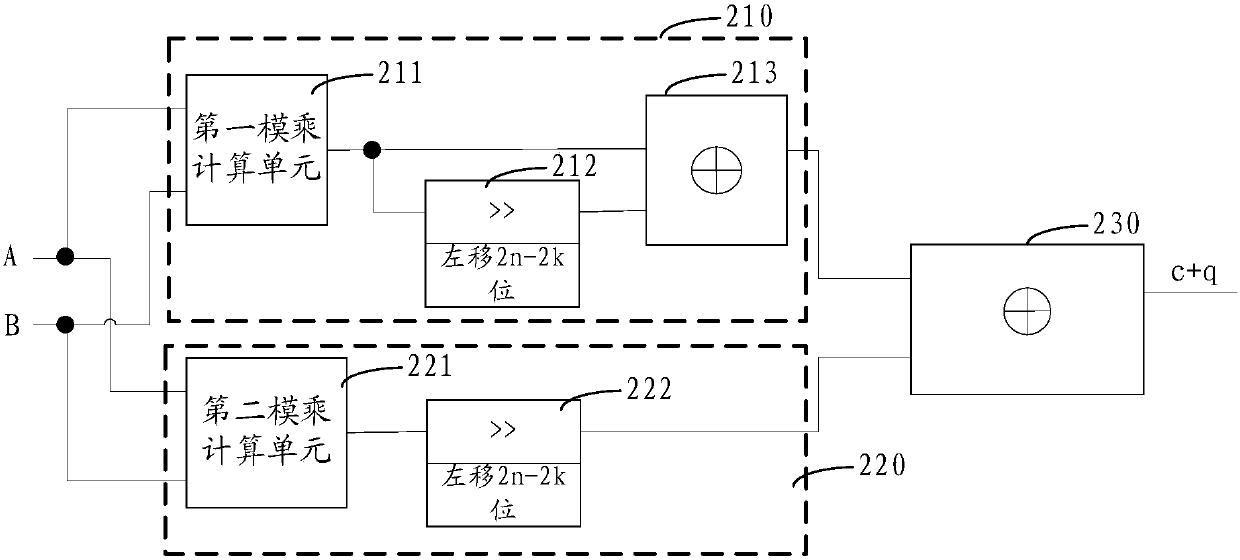
[0035] The polynomial base GF (2^n) multiplier of the present invention is used to utilize the circuit to calculate the element in the polynomial ring R[x] and product of . Among them, a i ,b i ∈R, R is a ring.
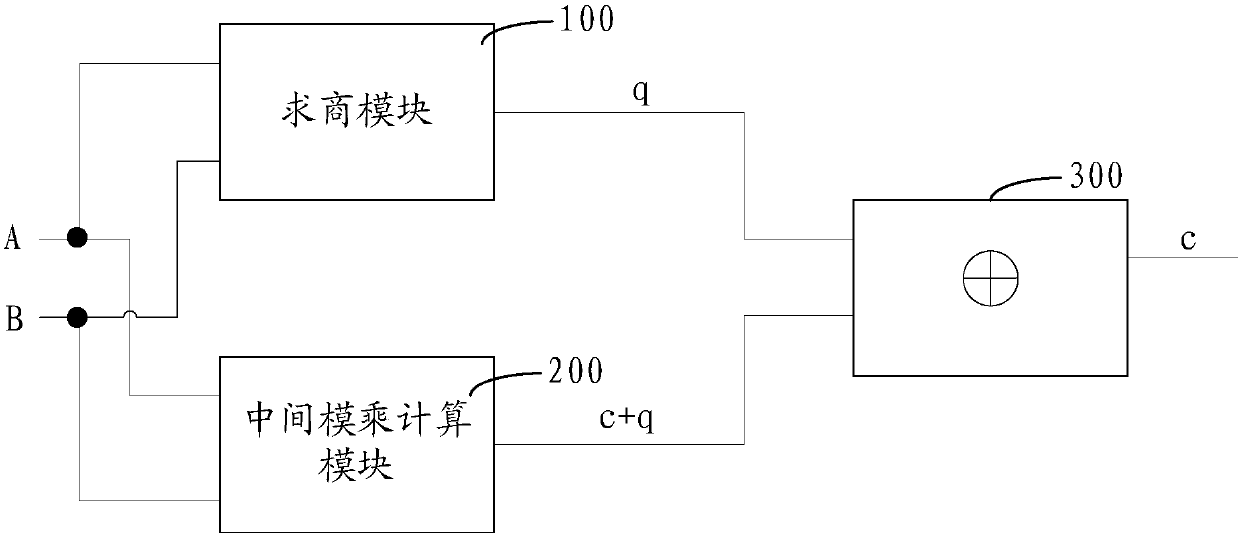
[0036] The multiplier of an embodiment of the present invention, such as figure 1 It includes a quotient seeking module 100 , an intermediate modular multiplication calculation module 200 and a summation module 300 .
[0037] Wherein, the quotient module 100 is used to calculate two polynomials for modular multiplication and The product AB...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com