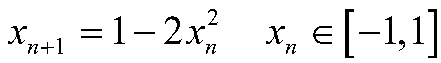Supercharge Your Innovation With Domain-Expert AI Agents!

Method for realizing random bit non-blind watermark based on chaos

An implementation method, a technology of random bits, applied in the fields of information security, image processing, and computer applications, which can solve the problems of different and unable to extract watermark information.

Inactive Publication Date: 2018-07-03
TIANJIN UNIV OF TECH & EDUCATION TEACHER DEV CENT OF CHINA VOCATIONAL TRAINING & GUIDANCE
View PDF0 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

If the embedding process and the extraction process use different keys, different position matrices will be generated, and the extraction process will extract the watermark information at a position different from the embedding position, so the correct watermark information cannot be extracted

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for realizing random bit non-blind watermark based on chaos
  • Method for realizing random bit non-blind watermark based on chaos
  • Method for realizing random bit non-blind watermark based on chaos

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

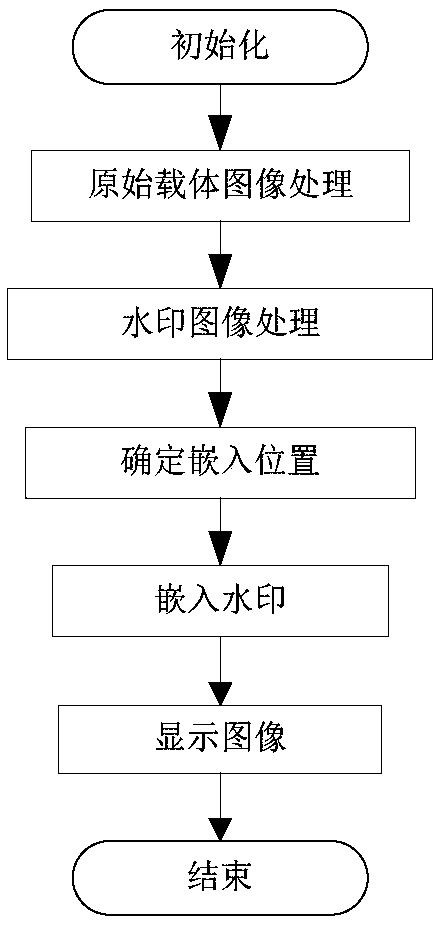
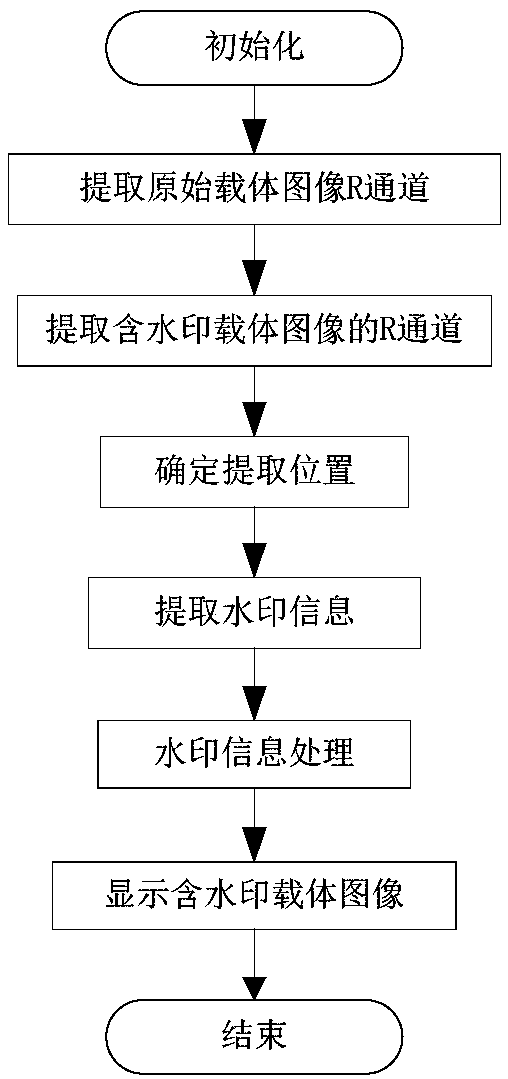
[0100] The random bit non-blind watermark is operated on each pixel in the carrier, and the position of the embedded watermark is not fixed. The specific implementation steps are divided into embedding process and extraction process.

[0101] For the convenience of understanding, the watermark here is only embedded in the R channel of the carrier image. In actual processing, the watermark can be embedded in multiple channels, and the method of embedding watermark in other channels is the same as that in R channel.

[0102] 1 Embedding process

[0103] The embedding process calculates the original watermark information with the carrier image and then embeds it into the carrier image.

[0104] (1) Original carrier image processing

[0105] Read in the original carrier image, obtain the size of the image, decompose it into channels, and divide it into R channel, G channel, and B channel.

[0106] For example, there is the original carrier image O, whose size is 4*4, which is ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The name of the patent of the invention is a method for realizing a random bit non-blind watermark based on chaos, which relates to the technical fields of image processing, computer application and information security. Watermark information is embedded into a carrier image by calculating the embedding positions of different bits through a chaotic system. During embedding, exclusive-OR operationis carried out on the watermark information and the bit value on a specific bit of a binary pixel value in a corresponding position (the coordinates of the pixels are the same) of the carrier image, and the operation result is embedded into the bit participating in operation in the carrier image. During extraction, the values on specific bits with the same binary pixel value in corresponding positions of the watermark-containing carrier image and the original carrier image are extracted, and exclusive-OR operation is carried out on the two values to extract the original watermark information.The method can be widely applied to the fields such as information hiding and copyright protection.

Description

technical field [0001] The patent of the present invention relates to the technical fields of image processing, computer application, information security and the like. Background technique [0002] This system uses chaotic system to generate random sequence. The widely used chaotic system is the Logi stic chaotic system, and its improved form is: [0003] [0004] The system is extremely sensitive to initial values, and a slightly different initial value can give completely different results. According to the characteristics of the chaotic system, a pseudo-random sequence can be generated, and a sequence between [0, 7] can be generated by processing the sequence. [0005] For example, if the initial value of a chaotic system is set to 0.98, a one-dimensional chaotic sequence can be obtained, and the first 16 values ​​of the chaotic sequence a are shown in Table 1. [0006] Table 1 Sequence a [0007] [0008] According to the formula of the chaotic sequence, the s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06T1/00
CPCG06T1/0021G06T2201/0061G06T2201/0065
Inventor 不公告发明人
Owner TIANJIN UNIV OF TECH & EDUCATION TEACHER DEV CENT OF CHINA VOCATIONAL TRAINING & GUIDANCE
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com