Check patentability & draft patents in minutes with Patsnap Eureka AI!

Hyperspectral hyperpixel segmentation method based on principal component weighted false color synthesis and color histogram driving

A technology of false color synthesis and color histogram, applied in image enhancement, image data processing, image analysis, etc., can solve problems such as large data redundancy, difficult real-time image segmentation, and high data dimensionality of hyperspectral images

Active Publication Date: 2018-08-24
HARBIN INST OF TECH
View PDF4 Cites 10 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to solve the problem of difficult real-time segmentation of images due to the high dimensionality of hyperspectral image data and the large number of data redundancy

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Hyperspectral hyperpixel segmentation method based on principal component weighted false color synthesis and color histogram driving
  • Hyperspectral hyperpixel segmentation method based on principal component weighted false color synthesis and color histogram driving
  • Hyperspectral hyperpixel segmentation method based on principal component weighted false color synthesis and color histogram driving

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

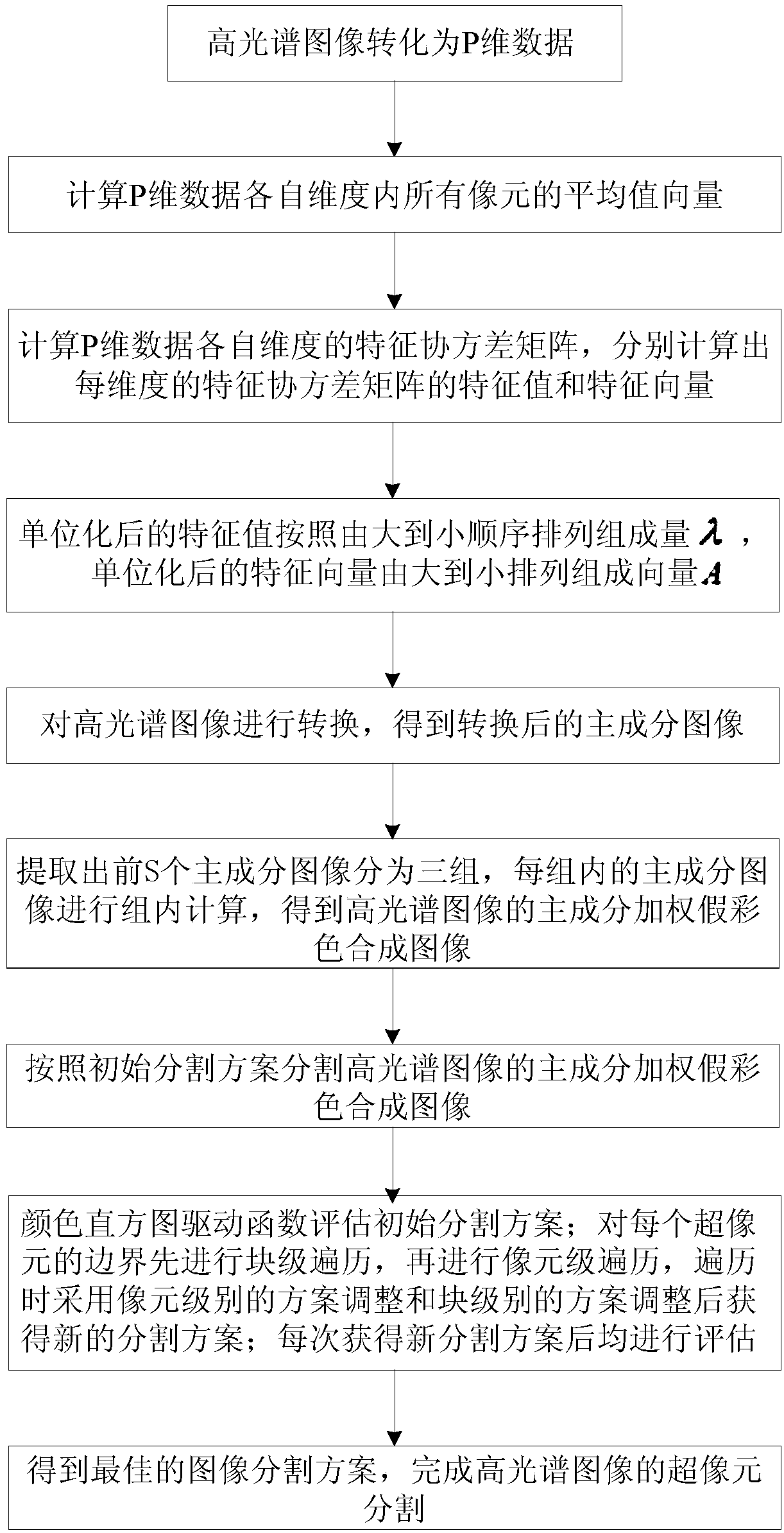
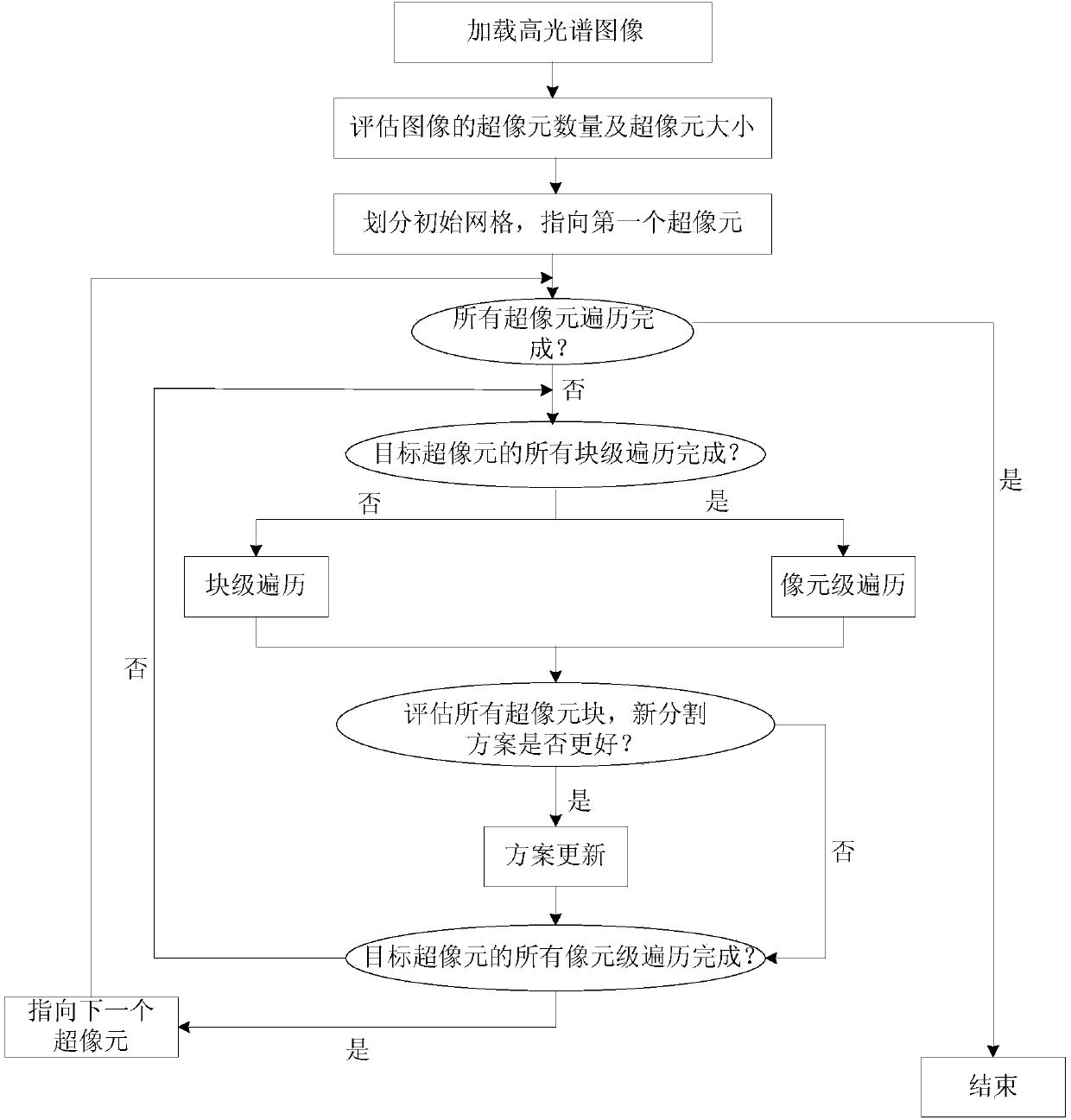
[0022] Specific implementation mode one: as figure 1 and 2 As shown, a hyperspectral super-pixel segmentation method based on principal component weighted false color synthesis and color histogram driving described in this embodiment is specifically carried out in accordance with the following steps:

[0023] Step 1: Perform principal component weighted false-color synthesis on the hyperspectral image data X of P-band M×N pixels, and convert the hyperspectral image into P-dimensional data; respectively calculate the average vector of all pixels in each dimension of the P-dimensional data ;

[0024] Step 2. Use the P-dimensional data obtained in step 1 and the average vectors of all pixels in the respective dimensions of the P-dimensional data to calculate the characteristic covariance matrix of the respective dimensions of the P-dimensional data, and calculate the characteristics of the characteristic covariance matrix of each dimension Values ​​and eigenvectors; unitize the...

specific Embodiment approach 2

[0033]Specific implementation mode two: the difference between this implementation mode and specific implementation mode one is: the specific process of step one is:

[0034] For hyperspectral image data X=(x 1 ,x 2 ,...x i ,...,x M×N )=(X 1 ,X 2 ,...,X j ,...,X P ) T Perform principal component weighted false color synthesis, where X is a (M×N)×P dimensional matrix, x i Represents the i-th pixel in the hyperspectral image, i=1,2,...,M×N, that is, convert the M×N pixel matrix into a (M×N)×1 pixel column vector, X j Indicates the jth dimension of the image, where j=1,2,...,P;

[0035] Calculate the mean vector of all pixels in the respective dimensions of the P-dimensional data:

[0036]

[0037] Represents the mean vector of all pixels in the hyperspectral image data in each dimension.

[0038] In this embodiment, the hyperspectral image is converted into P-dimensional high-dimensional data, and by calculating the M×N groups of data relative to the mean The a...

specific Embodiment approach 3

[0039] Specific implementation mode three: the difference between this implementation mode and specific implementation mode two is: the specific process of step two is:

[0040] The feature covariance matrix of each dimension of hyperspectral image data is:

[0041]

[0042] The diagonal elements of the characteristic covariance matrix C represent the variance of each dimension; the eigenvalues ​​and eigenvectors of the covariance matrix C of each dimension are calculated respectively, and the eigenvalues ​​and eigenvectors of the characteristic covariance matrix C of each dimension are unitized, and the unit The transformed eigenvalue λ j and the eigenvector a j Arrange according to the order from large to small to obtain the vector λ=(λ 1 ,λ 2 ,...,λ P ) and the vector A=(a 1 ,a 2 ,...,a P ).

[0043] The off-diagonal elements of the covariance matrix measure the degree of simultaneous change between different bands. The larger the correlation coefficient, the gre...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A hyperspectral hyperpixel segmentation method based on principal component weighted false color synthesis and color histogram driving belongs to the technical field of hyperspectral image segmentation. The method solves the problem that the real-time segmentation of the image is difficult due to high dimensionality and high data redundancy of the hyperspectral image data. The method comprises putting the main spectral information of the hyperspectral image into a false color image, and reduces the dimension of the hyperspectral data; after dividing the principal component weighted false colorcomposite image into grid regions, performing, by using a pixel scale and a block scale, traversal iteration on the boundary of each superpixel of the divided principal component weighted false colorcomposite image, and obtaining a new image segmentation scheme after each complete iteration; and using a histogram driving function to evaluate the new segmentation scheme after each complete iteration to finally obtain the best image segmentation scheme to achieve superpixel segmentation of the hyperspectral image. The method can be applied to the field of segmentation of hyperspectral images.

Description

technical field [0001] The invention belongs to the technical field of hyperspectral image segmentation, and in particular relates to a hyperspectral super-pixel segmentation method based on principal component weighted false color synthesis and color histogram driving. Background technique [0002] Hyperspectral remote sensing is one of the most important developments in the field of remote sensing since the 1980s. It has become a hot topic in the field of international remote sensing technology in the 1990s, and it will also be the frontier technology of remote sensing in the next few decades. Hyperspectral images have high spectral resolution and provide rich information about the types of ground objects. Since hyperspectral images have many bands, and each band can be regarded as a grayscale image, therefore, for each When individual images are analyzed and studied separately, hyperspectral image segmentation is required. Traditional hyperspectral image segmentation met...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06T7/11G06T7/90
CPCG06T2207/10024G06T2207/10036G06T7/11G06T7/90
Inventor 林连雷王建峰周祝旭
Owner HARBIN INST OF TECH
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com