Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Nonlinear Filtering Method with Random Occurrence Uncertainty and Quantized Measurements

A nonlinear filtering and uncertainty technology, which is applied in the field of nonlinear filtering, can solve the problems of large filtering error and the inability of filtering technology to deal with uncertainty and quantitative measurement at the same time, and achieve the effect of reducing the relative error of filtering

Active Publication Date: 2022-03-04
HARBIN UNIV OF SCI & TECH
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The present invention provides a non-linear filtering method with random uncertainty and quantitative measurement in order to solve the problem that the existing filtering technology cannot deal with random uncertainty and quantitative measurement at the same time, resulting in large filtering errors

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Nonlinear Filtering Method with Random Occurrence Uncertainty and Quantized Measurements
  • A Nonlinear Filtering Method with Random Occurrence Uncertainty and Quantized Measurements
  • A Nonlinear Filtering Method with Random Occurrence Uncertainty and Quantized Measurements

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

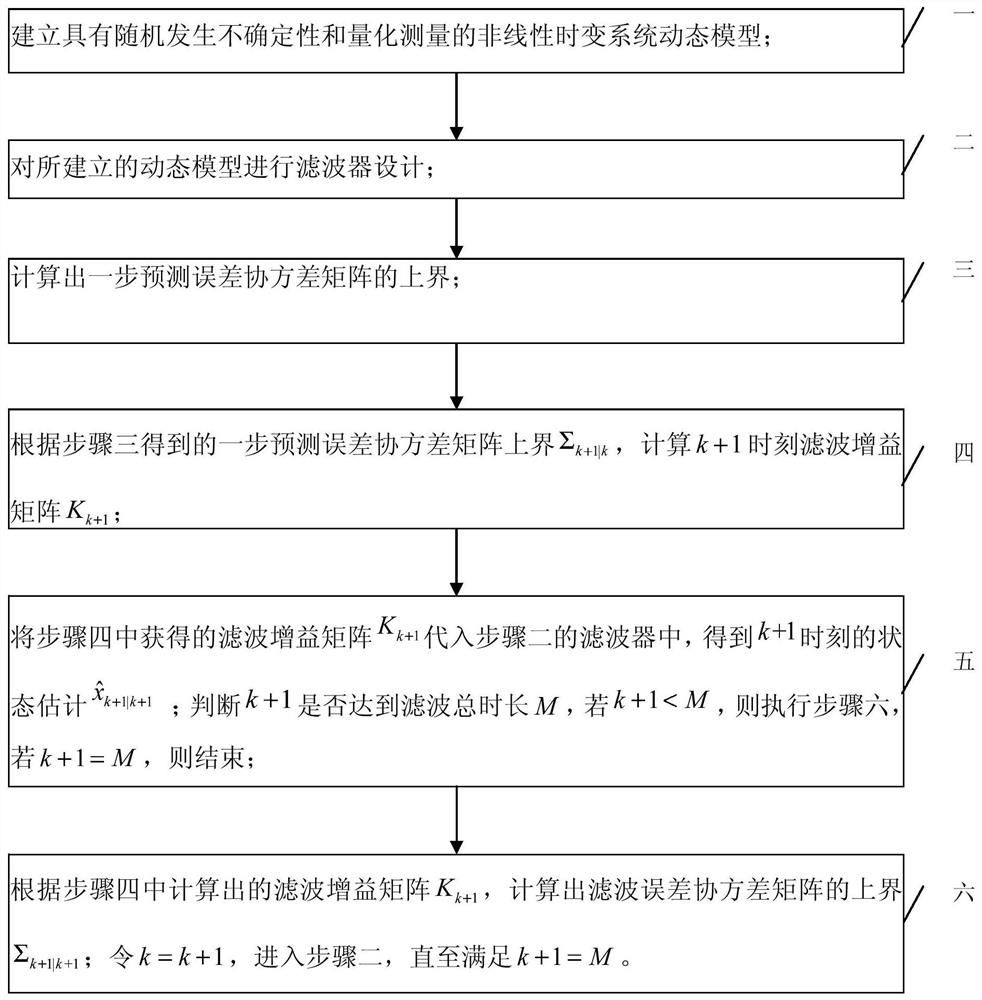
[0023] Specific implementation mode one: combine figure 1 The present embodiment is described. A non-linear filtering method with stochastic uncertainty and quantitative measurement provided in this embodiment specifically includes the following steps:

[0024] Step 1. Establishing a nonlinear time-varying system dynamic model with stochastic uncertainties and quantitative measurements;

[0025] Step 2, performing filter design on the dynamic model established in step 1;

[0026] Step 3. Calculate the upper bound Σ of the one-step forecast error covariance matrix according to the one-step forecast error and mathematical processing method k+1|k ;

[0027] Step 4. According to the upper bound Σ of the one-step forecast error covariance matrix obtained in step 3 k+1|k , calculate the filter gain matrix K at time k+1 k+1 ;

[0028] Step five, the filter gain matrix K obtained in step four k+1 Substitute into the filter in step 2 to get the state estimation at time k+1

[...

specific Embodiment approach 2

[0031] Specific embodiment 2: The difference between this embodiment and specific embodiment 1 is that the state space form of the nonlinear time-varying system dynamic model with stochastic uncertainty and quantitative measurement described in step 1 is:

[0032] x k+1 =(A k +α k ΔA k )x k +f(x k ,ξ k )+B k ω k (1)

[0033] the y k =C k x k +ν k (2)

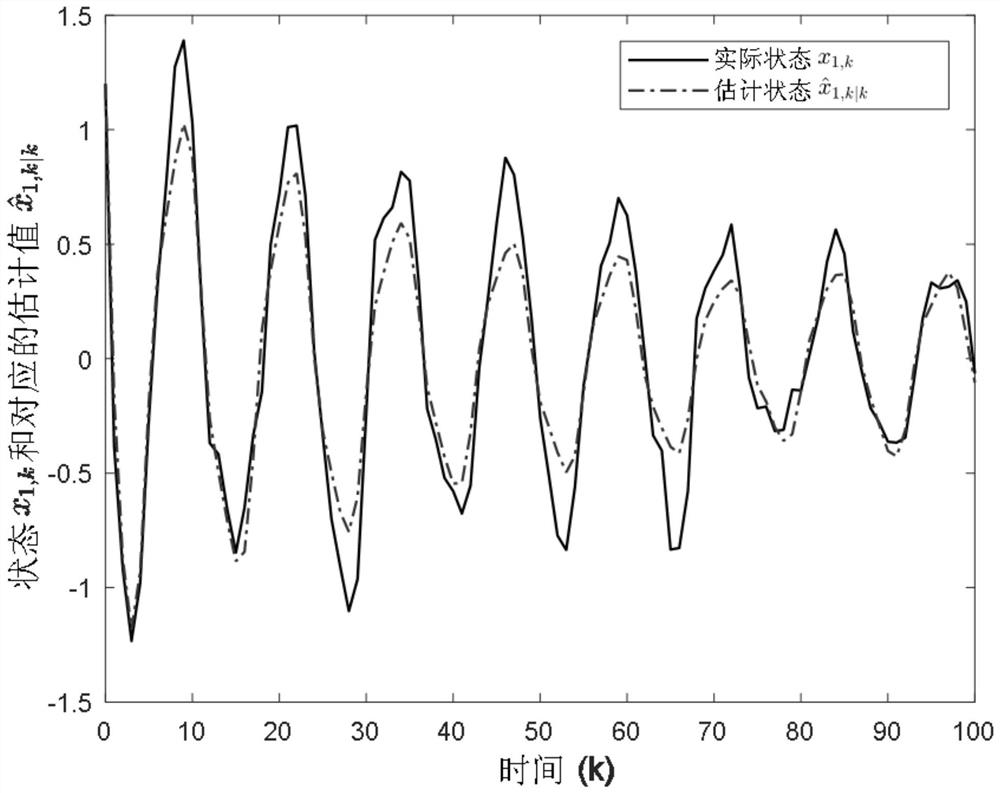
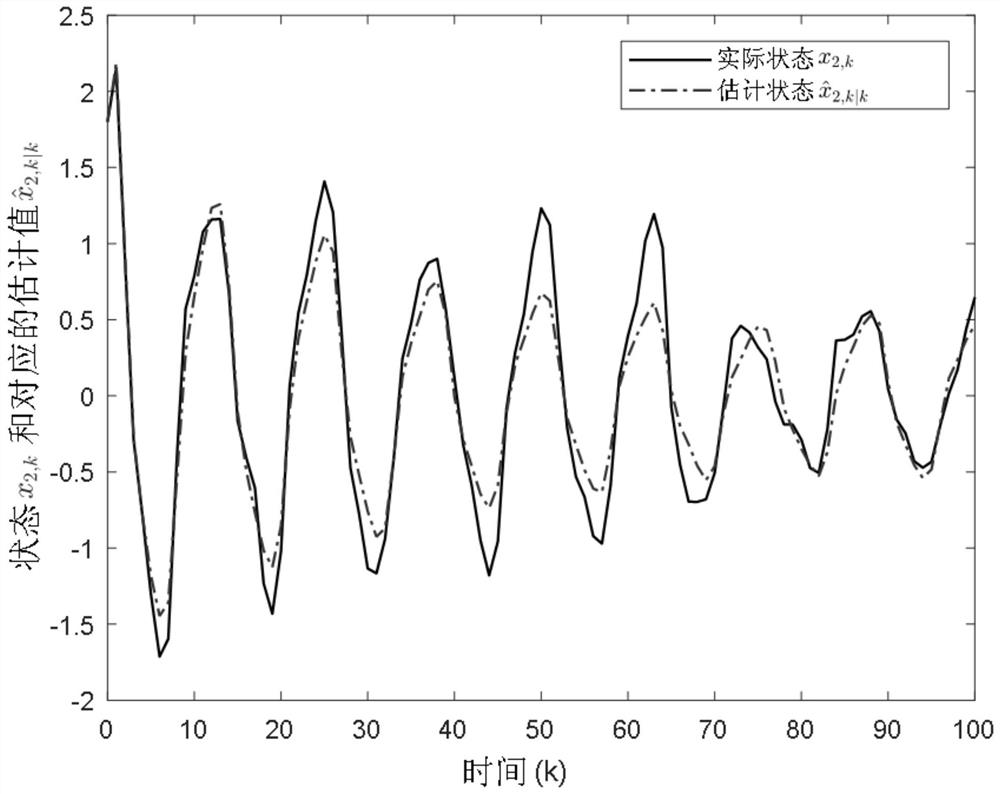
[0034] where x k is the state vector in the dynamic model of the nonlinear time-varying system at time k, x k+1 is the state vector in the dynamic model of the nonlinear time-varying system at time k+1; y k is the measurement output vector of the system at time k; A k is the system matrix of the nonlinear time-varying system at time k, B k is the noise distribution matrix of the nonlinear time-varying system at time k, C k is the measurement matrix of the nonlinear time-varying system at time k, A k , B k and C k is a known matrix; ξ k is a Gaussian white noise sequence with zero mean; ω k is the expecta...

specific Embodiment approach 3

[0037] Specific embodiment three: the difference between this embodiment and specific embodiment two is that the specific process of filter design described in step two includes:

[0038] First, for the measured output y k Quantize to get q(y k ):

[0039] Where q(·) means to quantify ·, q j Indicates the jth component of q, is the vector y k The jth component of , is the jth logarithmic quantizer; j=1,2,...,m;

[0040] After being processed by the quantizer, the measured values ​​received at the filter end are:

[0041]

[0042] Among them, Λ k :=diag{λ k,1 ,λ k,2 ,...,λ k,m}, λ k,j is a random variable that obeys the Bernoulli distribution, satisfying and in is lambda k,j The mathematical expectation of , Prob( ) represents the probability of occurrence of the event ;

[0043] Construct the following filter formula:

[0044]

[0045]

[0046] in, for x k The state estimation vector at time k, is the estimated value of the state at time k+1...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a nonlinear filtering method with random occurrence uncertainty and quantitative measurement, which belongs to the technical field of state estimation. The present invention first establishes the nonlinear time-varying system dynamic model with stochastic uncertainty and quantitative measurement, and performs filter design on the dynamic model; then calculates the upper bound of the one-step forecast error covariance matrix; through the one-step forecast error covariance matrix The upper bound is calculated to obtain the filter gain matrix K k+1 ; Then the filter gain matrix K k+1 Substitute into the filter in step 2 to get the state estimation at time k+1 and according to the calculated filter gain matrix K k+1 , calculate the upper bound Σ of the filter error covariance matrix k+1|k+1 ; Repeat the above steps until the total filter duration is satisfied. The invention solves the problem that the existing filtering technology cannot simultaneously deal with the uncertainty of random occurrence and the quantitative measurement, which further leads to large filtering errors. The invention can be used for filtering of nonlinear time-varying systems.

Description

technical field [0001] The invention relates to a nonlinear filtering method with random occurrence uncertainty and quantitative measurement, belonging to the technical field of state estimation. Background technique [0002] Filtering is the operation of filtering out the frequency of a specific band in the signal, and it is a basic and important measure for selecting signals and suppressing interference. Filtering is an important research problem in control systems, and it is widely used in signal estimation tasks in radar ranging, target tracking systems, image acquisition and other fields. Due to data redundancy and channel bandwidth limitations, when data is transmitted to the filter end through the network, it usually leads to some network-induced phenomena, such as network congestion, delay, etc., and it is necessary to design a filtering algorithm that adapts to these network-induced phenomena. . [0003] The current existing methods cannot deal with the robust fil...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H03H21/00
CPCH03H21/0016H03H21/0043
Inventor 胡军赵文杰贾朝清崔云菲贾凤娇高铭
Owner HARBIN UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com