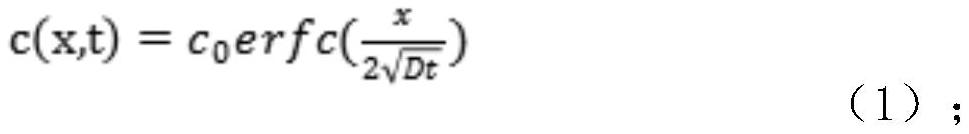Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Method for Measuring Diffusion Coefficient of Porous Materials and Predicting Adsorption Capacity

A technology for porous materials and diffusion coefficients, applied in measuring devices, analytical materials, instruments, etc., can solve the problems of inapplicability of the measurement of the diffusion coefficients of porous materials, and achieve the effect of accurate and quantitative measurement of diffusion coefficients, and the method is simple and easy

Active Publication Date: 2021-09-03
朗缪环保科技(天津)有限公司
View PDF11 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] However, the method reported above is not suitable for the measurement of the diffusion coefficient of porous materials

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Method for Measuring Diffusion Coefficient of Porous Materials and Predicting Adsorption Capacity
  • A Method for Measuring Diffusion Coefficient of Porous Materials and Predicting Adsorption Capacity
  • A Method for Measuring Diffusion Coefficient of Porous Materials and Predicting Adsorption Capacity

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

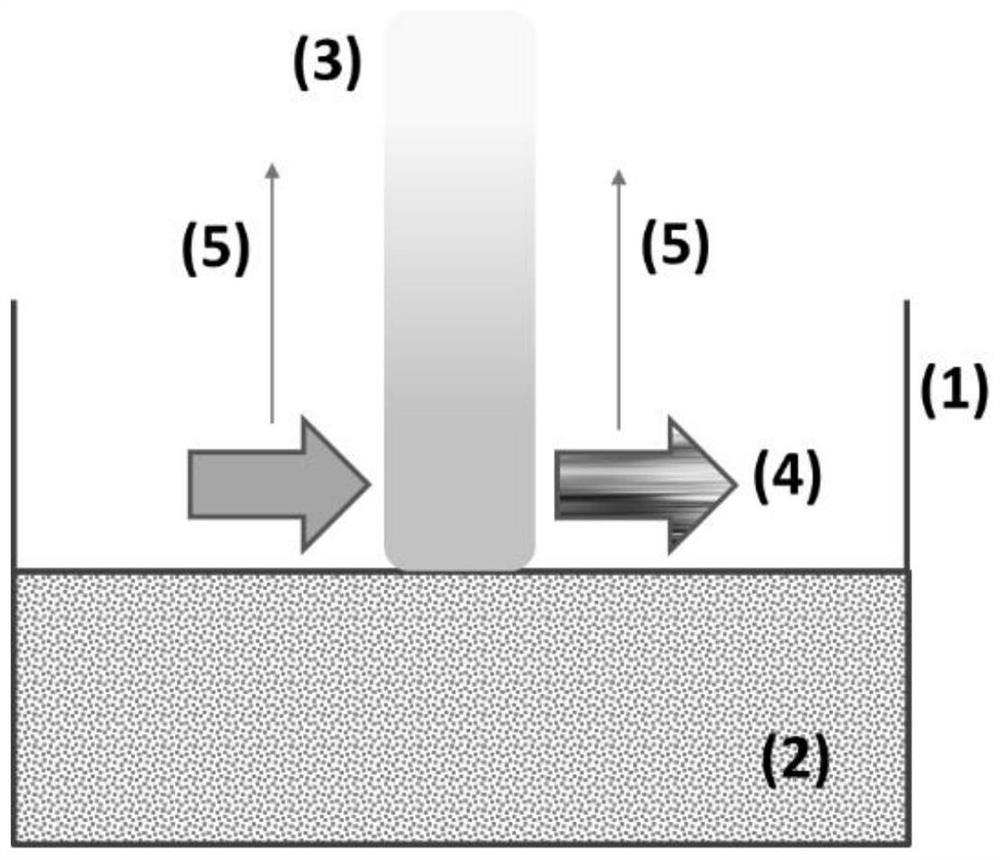
[0051] In the container to be tested, the volume of the adhesive solution is much larger than the volume of the porous material, which can be considered that the concentration of the absorbent solution is substantially constant, maintained at C. 0 .

[0052] The concentrations c (x, t) at different times and different locations are tested by spectral method, and multi-set value is recorded, and three-dimensional graphics are drawn.

[0053] Through Phi-second law, the concentration under one-dimensional diffusion conditions of fixed initial concentrations with X and T regulations are determined by the following complementary error functions, as shown in the formula (1):

[0054]

[0055] The complementary error function can be expanded through the Taylor level to retain 2 as an example, and the concentration C is approximated as the equation (2):

[0056]

[0057] As 0 In the case of determining, the value of the diffusion coefficient D can be fitted to the value of the multi-...

Embodiment 2

[0064] Place a trihydroxy-tuberculous solution into a container, the volume of the adhesive solution is much larger than the volume of the porous material, which can be considered that the concentration of the adhesion solution is substantially constant, maintained at C. 0 .

[0065] The concentrations c (x, t) at different times and different locations are tested by spectral method, and multi-set value is recorded, and three-dimensional graphics are drawn.

[0066] Through Phich's second law, the concentration under one-dimensional diffusion conditions of fixed initial concentrations is determined by the following complementary error function as follows. The complementary error function can be expanded by the Taylor level, after 2 items, by the above-described multi-group C-T data, the value of the diffusion coefficient D can be fitted.

[0067] The diffusion quality in this embodiment is a trihydroxybone, the solvent is ethanol, which is fixed to 0.3 mol / L, the porous material...

Embodiment 3

[0070] In the case where the solution to be tested is placed into the container, the volume of the adhesion solution is much larger than the volume of the porous material, which can be considered that the concentration of the adhesion solution is substantially unchanged and maintained at C. 0 .

[0071] The concentrations c (x, t) at different times and different locations are tested by spectral method, and multi-set value is recorded, and three-dimensional graphics are drawn.

[0072] Through Phich's second law, the concentration under one-dimensional diffusion conditions of fixed initial concentrations is determined by the following complementary error function as follows. The complementary error function can be expanded by the Taylor level, after 2 items, by the above-described multi-group C-T data, the value of the diffusion coefficient D can be fitted.

[0073] The diffusion quality in this embodiment is Cucl 2 The solvent is water, and its fixed initial concentration is 0.3 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the field of detection of porous materials and provides a method for measuring the diffusion coefficient of porous materials. One end of the material to be tested is soaked in an adsorbed solution with a fixed concentration, and by measuring the concentration distribution at different times and positions in the material, Through the approximate one-dimensional diffusion model and Fick's second law, the space-time two-dimensional image is fitted to obtain the diffusion coefficient. In the present invention, the adsorption amount can also be obtained through the measured diffusion coefficient and concentration function integration at a certain moment, and the adsorption concentration can also be obtained through diffusion for a long enough time to calculate the adsorption amount, which is convenient for the design and production of composite materials. The method provided by the invention is simple and easy, can measure the diffusion coefficient more accurately and predict the adsorption amount, and is of great significance to the testing, design, industrial production, adsorption or slow-release application of nanocomposite materials and the like.

Description

Technical field [0001] The present invention relates to the technical field of detection of the porous material, porous material and particularly to a method for predicting the diffusion coefficient and adsorption measurements. Background technique [0002] Porous material, in particular nano-porous material microstructure fine, high surface active, adjustable surface properties, is rich in the diffusion channel, very suitable adsorbent and sustained release materials. Adsorption and release process, the diffusion coefficient is an important parameter, which determines the rate of adsorption, release rate and release time of the effective key performance. However, to measure the diffusion coefficient, the concentration necessary to measure a plurality of sets of data with time and position, five groups theoretically required concentration, time and experimental parameters in order to determine the three-dimensional coordinates, in fact, almost impossible to measure the complete p...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01N13/00
CPCG01N13/00
Inventor 周非沈天弘孙士杰倪星元
Owner 朗缪环保科技(天津)有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com