Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Seismic data interpolation method and device

A technology of seismic data and interpolation method, which is applied in the direction of seismic signal processing, etc., can solve the problems of large amount of calculation, slow calculation speed, large amount of seismic data interpolation data, etc., and achieve the effect of improving calculation efficiency and interpolation quality

Active Publication Date: 2020-07-31
HEBEI GEO UNIVERSITY
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] At present, seismic data interpolation faces problems such as large amount of data, large amount of calculation, slow calculation speed, and poor quality of interpolated data.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Seismic data interpolation method and device
  • Seismic data interpolation method and device
  • Seismic data interpolation method and device

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

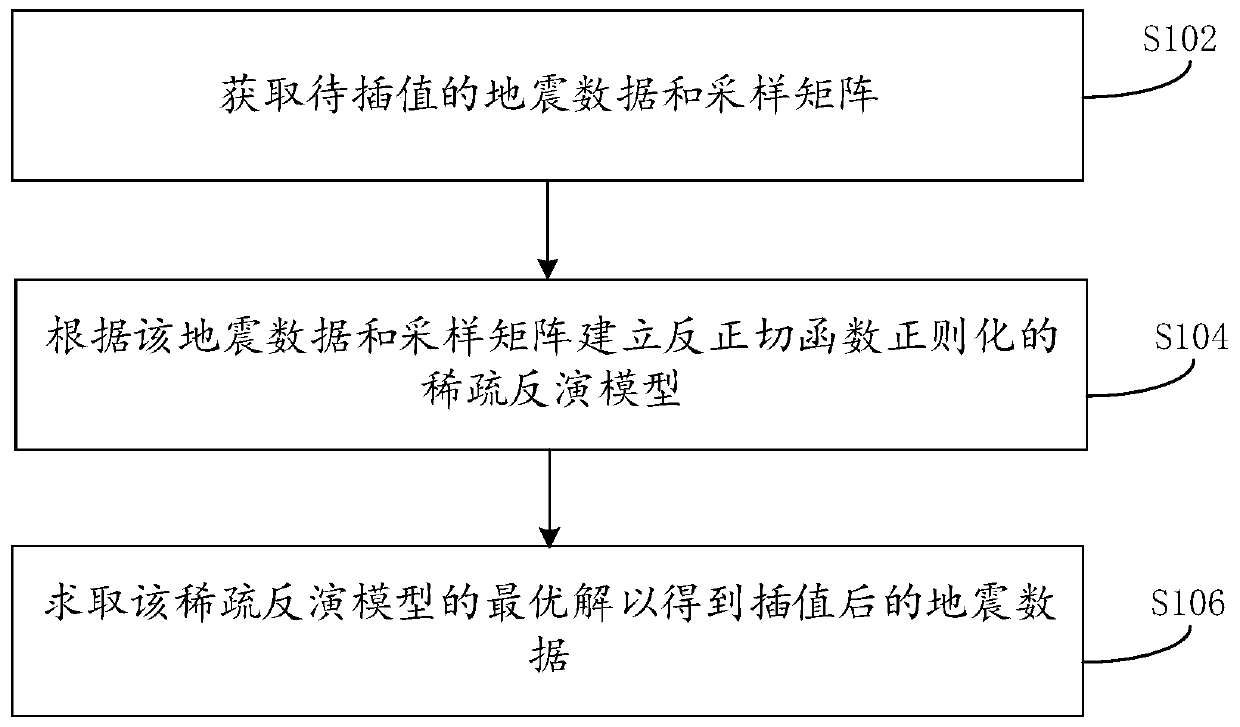
[0034] Such as figure 1 As shown, it is a schematic flow chart of a seismic data interpolation method provided by an embodiment of the present invention, consisting of figure 1 Visible, this method comprises the following steps:

[0035] Step S102: Obtain the seismic data to be interpolated and the sampling matrix.

[0036] Here, the seismic data to be interpolated may be seismic data obtained after preprocessing the acquired original seismic data. First, it is necessary to obtain the seismic data to be interpolated and the adoption matrix corresponding to the seismic data.

[0037] Step S104: Establish a sparse inversion model regularized by the arctangent function according to the seismic data and the sampling matrix.

[0038]Establishing a sparse inversion model based on the arctangent function belongs to the sparse inversion model regularized by non-convex functions. In one possible implementation, the sparse inversion model can be:

[0039]

[0040] In the formula,...

Embodiment 2

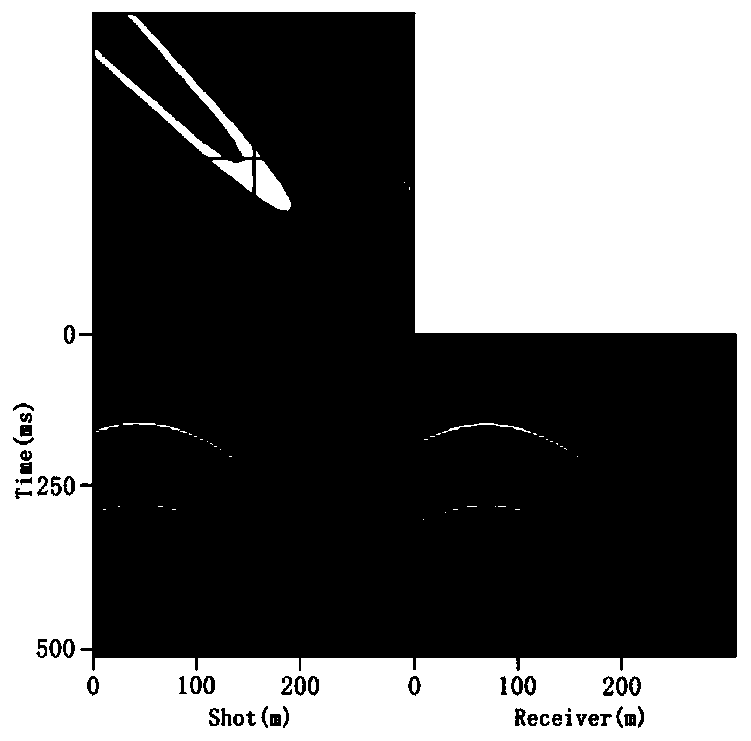
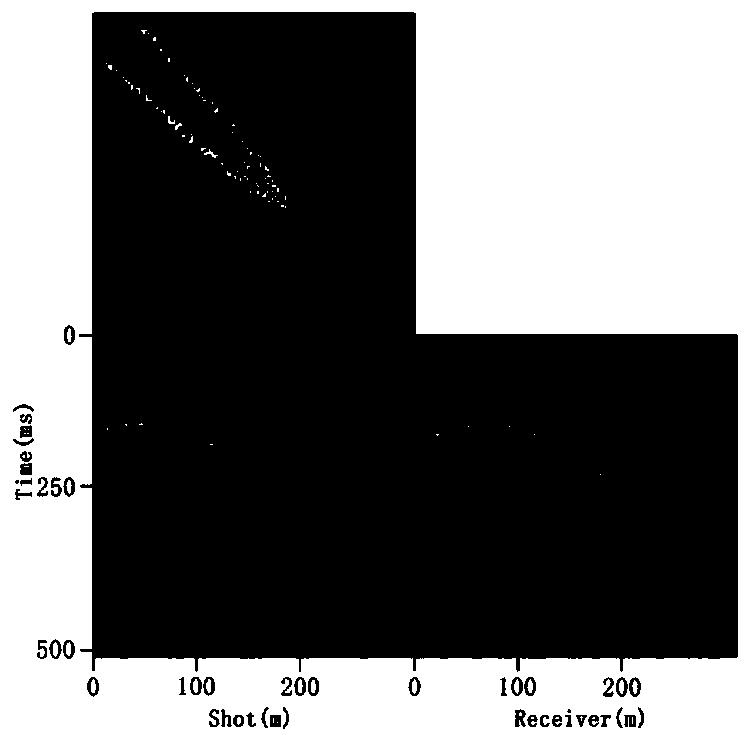
[0054] In order to better understand the seismic data interpolation method provided by the above-mentioned embodiment 1 and reflect the effect achieved by this method, this embodiment 2 introduces an example of interpolation using the above-mentioned seismic data interpolation method and a three-dimensional reconstruction example.

[0055] First, the interpolation steps using the above-mentioned seismic data interpolation method include:

[0056] Step 1: Input the seismic data d to be interpolated and the sampling matrix P;

[0057] Step 2: Establish a sparse inversion model regularized by the arctangent function.

[0058]

[0059] Among them, min means to minimize, J α (x) is an objective function, and C is the inverse of the curvelet transform, and x is the coefficient of the seismic data to be solved in the curvelet domain, and := means that it is defined as, Indicates an arctangent function of the i-th component of the coefficient of the seismic data in the curvelet ...

Embodiment 3

[0075] The embodiment of the present invention also provides a seismic data interpolation device, see Figure 5 , is a schematic diagram of the structure of the device, by Figure 5 It can be seen that the device includes a data acquisition module 51 , a sparse inversion model establishment module 52 , an interpolation seismic data acquisition module 53 and an interpolation seismic data output module 54 which are sequentially connected. Among them, the functions of each module are as follows:

[0076] Data acquisition module 51, used to acquire seismic data and sampling matrix to be interpolated;

[0077] The sparse inversion model building module 52 is used to establish a sparse inversion model regularized by the arctangent function according to the seismic data and the sampling matrix;

[0078] The interpolation seismic data obtaining module 53 is used to obtain the optimal solution of the sparse inversion model to obtain the interpolated seismic data;

[0079] The interp...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a seismic data interpolation method and device, and relates to the technical field of seismic data. The method comprises the following steps: obtaining seismic data to be interpolated and a sampling matrix; establishing a regularized sparse inversion model of an arc-tangent function according to the seismic data and the sampling matrix; and solving an optimal solution of thesparse inversion model to obtain the interpolated seismic data. The seismic data interpolation method and the device provided by the embodiment of the invention can effectively improve the calculation efficiency of seismic data interpolation and improve the interpolation quality.

Description

technical field [0001] The invention relates to the technical field of seismic data processing, in particular to a seismic data interpolation method and device. Background technique [0002] In seismic data processing, in addition to directly losing part of the information due to missing data, it may also cause noise in the subsequent processing process, resulting in various pulses in the seismic trace. Seismic data interpolation is an important means to obtain complete seismic data. Because seismic data has sparse representation in some transform domains, methods based on sparse transformation are often used to obtain complete seismic data. [0003] At present, seismic data interpolation faces problems such as large amount of data, large amount of calculation, slow calculation speed, and poor quality of interpolated data. Contents of the invention [0004] In view of this, the object of the present invention is to provide a seismic data interpolation method and device, w...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01V1/28
Inventor 曹静杰孙秀丽
Owner HEBEI GEO UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com