Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for elliptic curve signature in single-source network coding environment

A network coding and elliptic curve technology, applied in the field of network information security, can solve the problems of intra-generation pollution and inter-generation pollution, unstable network communication transmission, and system pollution without using elliptic curve signatures

Active Publication Date: 2019-08-02
XIAN UNIV OF POSTS & TELECOMM
View PDF4 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

It has great advantages in improving the overall performance of the network, but it also brings many pollution threats
Polluted nodes or unstable network communication transmission will pollute the system
These polluted information will be combined with other valid messages through coded transmission, so that the pollution will be transmitted to other messages, and eventually the communication system will collapse and the sink node will not be able to recover the original information.
These insecure factors largely limit the scope of application of network coding and hinder its application in real life.
[0003] The traditional elliptic curve digital signature method cannot resist intragenerational pollution and intergenerational pollution. At present, the elliptic curve signature method in the single-source network coding environment has not been used to resist the problem of intragenerational pollution and intergenerational pollution. How to use the single-source network coding environment Constructing elliptic curve homomorphic signatures is a technical problem that needs to be urgently solved in cryptography

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for elliptic curve signature in single-source network coding environment
  • Method for elliptic curve signature in single-source network coding environment
  • Method for elliptic curve signature in single-source network coding environment

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

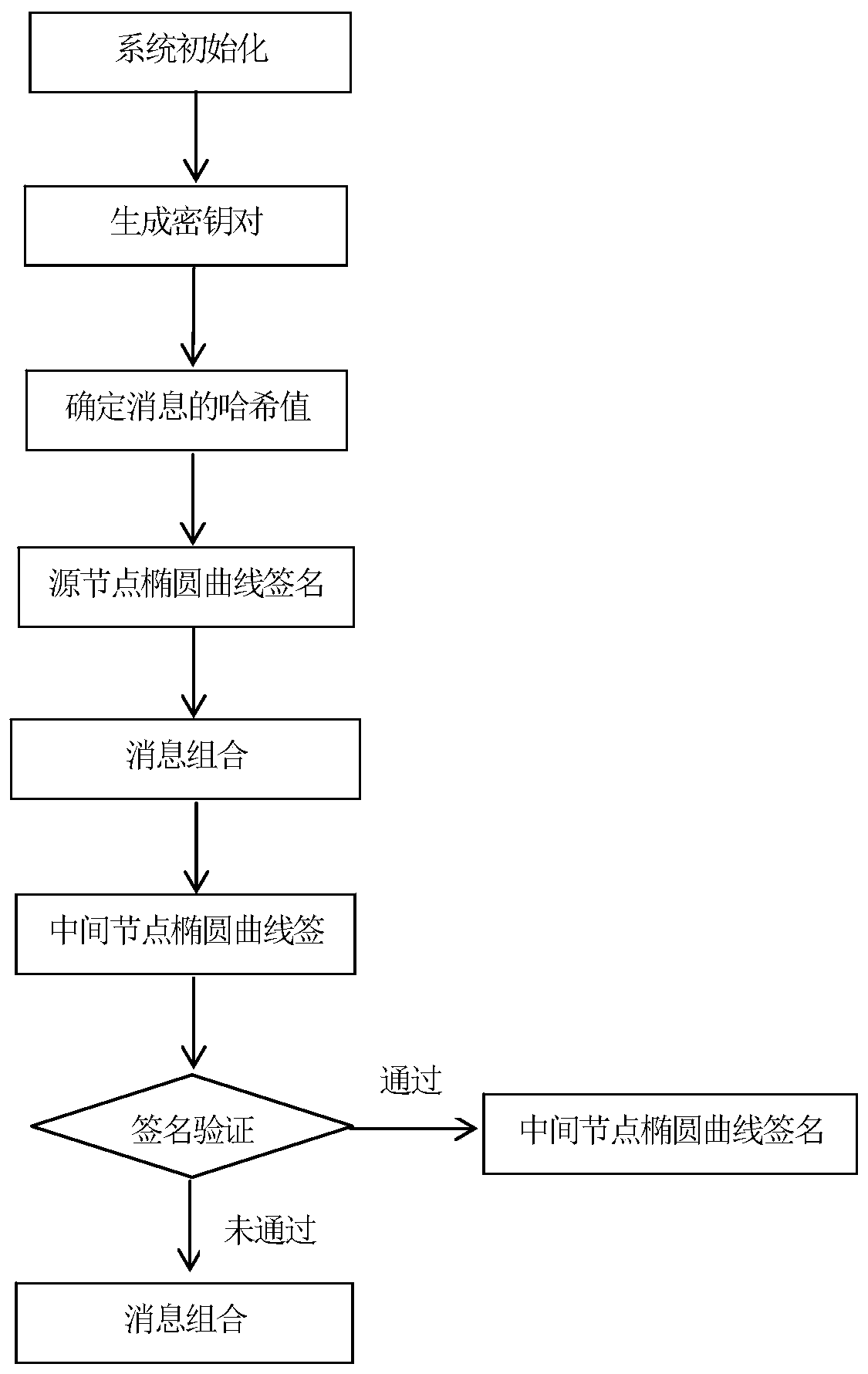
[0085] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+b mod q, the large prime number q is 1229388206666334394638158784063623508484129267643 as an example, the method of elliptic curve homomorphic signature of single-source network coding consists of the following steps (such as figure 1 shown):

[0086] A. System initialization

[0087] (A1) The trusted party defines a finite field F q Elliptic curve E on:

[0088] the y 2 ≡x 3 +ax+b

[0089] where a,b∈F q , q is a large prime number among finite positive integers, q is 1229388206666334394638158784063623508484129267643, satisfying 4a 3 +27b 2 ≠0 constant.

[0090] (A2) The trusted party sends the identifier I of the designated generation in the single-source network coding to the source node of the single-source network coding through a secure channel:

[0091] I={I 1 ,I 2 ,...,I n}

[0092] where n is a finite positive integer.

[0093] (A3) The trusted party selects a cryptographically secure Hash funct...

Embodiment 2

[0162] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+b mod q, the large prime q is 1449849246051449679173689466738734355356891578223 as an example, the method of elliptic curve homomorphic signature of single-source network coding consists of the following steps:

[0163] A. System initialization

[0164] (A1) The trusted party defines a finite field F q Elliptic curve E on:

[0165] the y 2 ≡x 3 +ax+b

[0166] where a,b∈F q , q is a large prime number among finite positive integers, q is 1449849246051449679173689466738734355356891578223, satisfying 4a 3 +27b 2 ≠0 constant.

[0167] (A2) The trusted party sends the identifier I of the designated generation in the single-source network coding to the source node of the single-source network coding through a secure channel:

[0168] I={I 1 ,I 2 ,...,I n}

[0169] where n is a finite positive integer.

[0170] (A3) The trusted party selects a cryptographically secure Hash function H G :

[0171] {0,1} * →G ...

Embodiment 3

[0185] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+bmodq, the large prime q is 1366294046726635493399336680549214898319268492501 as an example, the method of elliptic curve homomorphic signature of single-source network coding consists of the following steps:

[0186] A. System initialization

[0187] (A1) The trusted party defines a finite field F q Elliptic curve E on:

[0188] the y 2 ≡x 3 +ax+b

[0189] where a,b∈F q , q is a large prime number among finite positive integers, q is 1366294046726635493399336680549214898319268492501, satisfying 4a 3 +27b 2 ≠0 constant.

[0190] (A2) The trusted party sends the identifier I of the designated generation in the single-source network coding to the source node of the single-source network coding through a secure channel:

[0191] I={I 1 ,I 2 ,...,I n}

[0192] where n is a finite positive integer.

[0193] (A3) The trusted party selects a cryptographically secure Hash function H G :

[0194] {0,1} * →G 1...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for elliptic curve signature in a single-source network coding environment. The method comprises the steps of system initialization, generation of a single-source network coding key pair, determination of a Hash value of a message, elliptic curve signature of a source node, message combination, elliptic curve signature of an intermediate node and signature verification. The elliptic curve signature and the homomorphic Hash function are adopted, the verification process of the intermediate node is simplified, the calculation complexity is reduced, the energy consumption is reduced, and the generation identifier is introduced while the generation internal pollution is resisted, so that the inter-generation pollution is effectively resisted. The method has theadvantages of strong security, high calculation efficiency and the like, and can be popularized and applied in the single-source network coding.

Description

technical field [0001] The invention belongs to the technical field of network information security, and in particular relates to an elliptic curve signature method and a homomorphic hash function in single-source network coding and cryptography. Background technique [0002] In a traditional communication network, the intermediate nodes of the network can only forward the input data packets without any processing on the data content. Using network coding can not only greatly save network resources, but also improve network transmission rate, throughput and reliability, and reduce energy consumption. It has great advantages in improving the comprehensive performance of the network, but it also brings many pollution threats. Polluted nodes or unstable network communication transmission will pollute the system. These polluted information will be combined with other valid messages through coded transmission, so that the pollution will be transmitted to other messages, and eve...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/32
CPCH04L9/3252
Inventor 俞惠芳李雯
Owner XIAN UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com