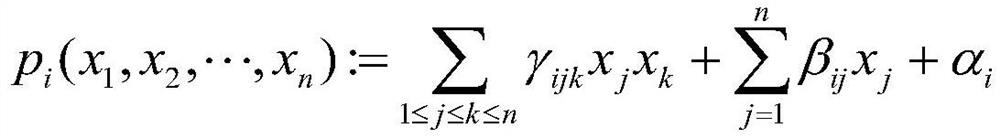Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A multivariate multi-signature approach with strongly designated verifiers in a certificateless environment

A designated verifier, multi-signature technology, applied in the field of network information security

Active Publication Date: 2020-11-10
XIAN UNIV OF POSTS & TELECOMM
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there is currently no multi-variable multi-signature method with a strong designated verifier in a certificateless environment. How to use the certificateless public key cryptosystem to construct a multi-variable multi-signature with a strong designated verifier is a technology that needs to be urgently solved in cryptography. question

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A multivariate multi-signature approach with strongly designated verifiers in a certificateless environment
  • A multivariate multi-signature approach with strongly designated verifiers in a certificateless environment
  • A multivariate multi-signature approach with strongly designated verifiers in a certificateless environment

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

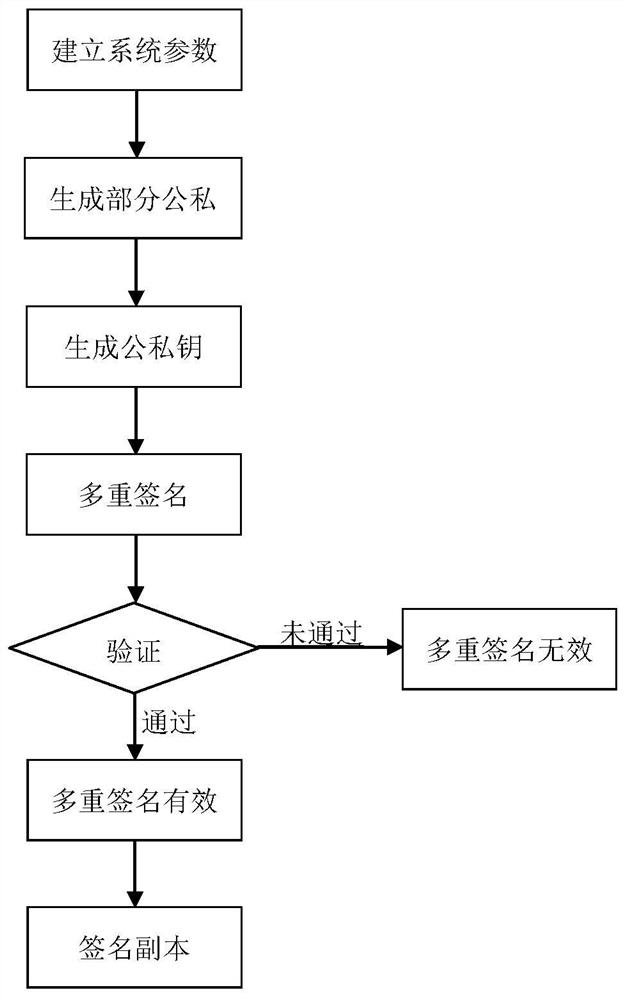
[0091] In this embodiment, the feature p is 2, and the order q is 2 8 , that is, the finite field F of 256, n is 42, and r is 24 multivariate equations as an example, the multivariate multi-signature method with a strong designated verifier in a certificateless environment consists of the following steps:

[0092] A. Establish system parameters

[0093] (A1) The key generation center defines a finite field F with feature p and order q. In this embodiment, p is 2 and order q is 2 8 , namely 256.

[0094] (A2) The key generation center defines n-element r multivariate equations on the finite field F. In this embodiment, n is 42, and r is 24:

[0095] P=(p 1 (x 1 ,x 2 ,...,x n ),…,p i (x 1 ,x 2 ,...,x n ),…,p r (x 1 ,x 2 ,...,x n ))

[0096] Each equation system p i is about the variable x being x 1 ,x 2 ,...,x n The nonlinear quadratic equation for , where i is 1,2,…,r:

[0097]

[0098] Among them, each coefficient α, β, γ and variable x are in the finite...

Embodiment 2

[0167] In this embodiment, the feature p is 2, and the order q is 2 8 , that is, the finite field F of 256, n is 30, and r is 25 multivariate equations as an example, the multivariate multi-signature method with a strong designated verifier in a certificate-free environment consists of the following steps:

[0168] A. Establish system parameters

[0169] (A1) The key generation center defines a finite field F with feature p and order q. In this embodiment, p is 2 and order q is 2 8 , namely 256.

[0170] (A2) The key generation center defines n-element r multivariate equations on the finite field F. In this embodiment, n is 30 and r is 25:

[0171] P=(p 1 (x 1 ,x 2 ,...,x n ),…,p i (x 1 ,x 2 ,...,x n ),…,p r (x 1 ,x 2 ,...,x n ))

[0172] Each equation system p i (i is 1,2,...,r) is about variable x being x 1 ,x 2 ,...,x n The nonlinear quadratic equation for :

[0173]

[0174] Among them, each coefficient α, β, γ and variable x are in the finite field ...

Embodiment 3

[0243] In this embodiment, the feature p is 2, and the order q is 2 9 That is, the finite field F of 512, n is 30, r is 25 multivariate equations as an example, the multivariate multi-signature method with a strong designated verifier in a certificateless environment consists of the following steps:

[0244] A. Establish system parameters

[0245] (A1) The key generation center defines a finite field F with feature p and order q. In this embodiment, p is 2 and order q is 2 9 , namely 512.

[0246] (A2) The key generation center defines n-element r multivariate equations on the finite field F. In this embodiment,

[0247] P=(p 1 (x 1 ,x 2 ,...,x n ),…,p i (x 1 ,x 2 ,...,x n ),…,p r (x 1 ,x 2 ,...,x n ))

[0248] Each equation system p i is about the variable x being x 1 ,x 2 ,...,x n The nonlinear quadratic equation of , where i is 1,2,…,r, n and r are finite positive integers:

[0249]

[0250] Among them, each coefficient α, β, γ and variable x are in t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A multi-variable multi-signature method with a strong designated verifier in a certificateless environment, which consists of the steps of establishing system parameters, generating part of public and private keys, generating public and private keys, multi-signature, verification, and signature copy steps. The present invention combines the non-certificate public key cryptosystem and the multi-signature method with a strong designated verifier under the multi-variable public key cryptosystem, and proposes a multi-variable multi-signature method with a strong designated verifier in a certificate-free environment. Using the certificateless public key cryptography technology, it solves the certificate management problem under the traditional cryptography system and the key escrow problem under the identity cryptography system. The length of the multi-signature has nothing to do with the number of signers. The verification time of the multi-signature is consistent with the verification time of a single partial signature. It has the advantages of small amount of calculation for signature and verification, and resistance to quantum computing attacks. It can be applied to technical fields such as vehicle networks and education systems. .

Description

technical field [0001] The invention belongs to the technical field of network information security, and specifically relates to cryptography or a multivariable public key cryptosystem or a certificateless public key cryptosystem or a multi-signature method with a strong designated verifier. Background technique [0002] Strong designated verifier multi-signature is a group-oriented signature that allows multiple signers to sign the same message, and only the verifier designated by the signer can verify the validity of the signature. Strong designated verifier multi-signature can be applied to e-shopping, e-auction and intellectual property protection. Currently, the security of most multi-signatures with strongly designated verifiers is mainly based on the intractability of the large integer factorization problem or the discrete logarithm problem. The emergence of quantum algorithms and the imminent birth of quantum computers will pose a certain threat to the strong design...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/32H04L9/08H04L9/06
CPCH04L9/0643H04L9/0819H04L9/0861H04L9/3255
Inventor 王之仓俞惠芳付帅凤
Owner XIAN UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com