Supercharge Your Innovation With Domain-Expert AI Agents!

Iron loss calculation method based on local hysteresis loop model

A technology of hysteresis loop and calculation method, applied in complex mathematical operations, design optimization/simulation, etc., can solve the problems of inaccurate hysteresis loss and partial hysteresis loop not closing, and achieve the effect of accurate core loss

Active Publication Date: 2022-04-05
HARBIN INST OF TECH
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The present invention aims to solve the problem that the local hysteresis loop described by the traditional inverse J-A model is not closed, resulting in inaccurate hysteresis loss acquisition. Now, a method for calculating iron loss based on the local hysteresis loop model is proposed.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Iron loss calculation method based on local hysteresis loop model
  • Iron loss calculation method based on local hysteresis loop model
  • Iron loss calculation method based on local hysteresis loop model

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

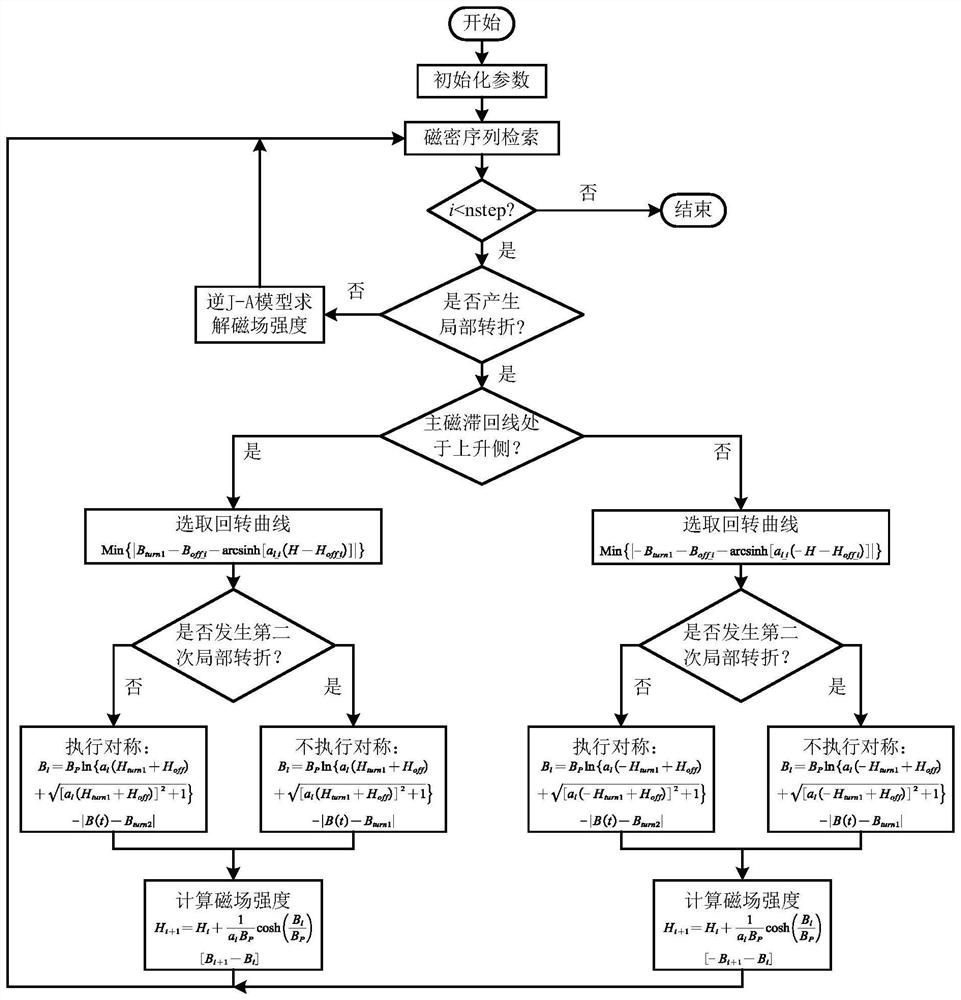
[0035] Specific implementation mode one: combine figure 1 Describe this embodiment, this embodiment is an iron loss calculation method based on a local hysteresis loop model, including the following steps:

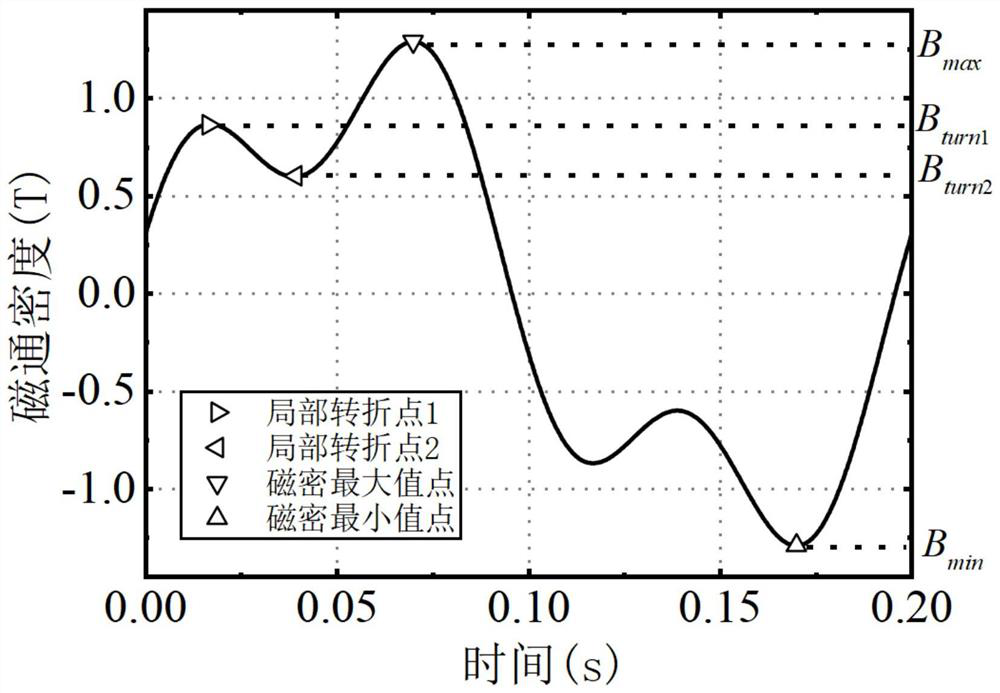
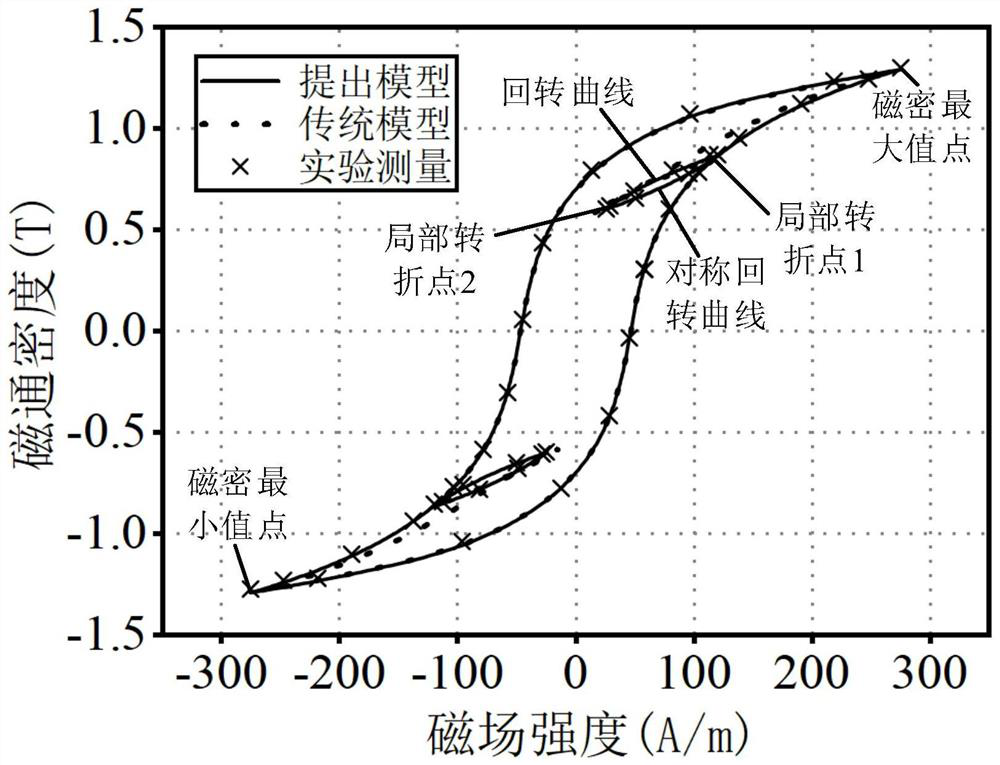
[0036] Step 1. Obtain the magnetic flux density sequence of the silicon steel sheet and the hysteresis loop data. The hysteresis loop includes a main hysteresis loop and a gyration curve, and the main hysteresis loop includes n magnetic flux densities;

[0037] Step 2. Judging whether the i-th magnetic flux density on the main hysteresis loop has a local turning point, wherein, the initial value of i is 1, i=1,2,...,n, if no local turning point occurs, then Use the inverse J-A model to calculate the magnetic field intensity corresponding to the i-th magnetic flux density, and re-retrieve the magnetic flux density sequence until a local turning point occurs, record the point when the local turning point occurs as the first local turning point, and the first local If the tu...

specific Embodiment approach 2

[0062] Embodiment 2: The difference between this embodiment and Embodiment 1 is that the inverse J-A model in the step 2 is:

[0063]

[0064] In the formula, t is the time of the previous step; Δt is the time change from the previous step to the current step; B is the magnetic flux density, H is the magnetic field intensity, and the magnetic flux density B is known and given in the form of time series; B(t) is the magnetic flux density of the previous step, B(t+Δt) is the magnetic flux density of the current step, ΔB is the change of the magnetic flux density from the previous step to the current step, H(t) is the magnetic field intensity of the previous step; H(t +Δt) is the magnetic field strength of the current step, M is the magnetization strength, H e , B e is the effective magnetic field strength and effective magnetic flux density, M an is the ideal magnetization fitted by the Langevin equation, M irr is the reversible magnetization, a, α, c, k, M s are the five...

specific Embodiment approach 3

[0067] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is that the direction coefficient δ is:

[0068]

[0069] Other steps are the same as those in Embodiment 1 or 2.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an iron loss calculation method based on a local hysteresis loop model, and belongs to the field of iron loss calculation. The invention aims to solve the problem that the acquired hysteresis loss is inaccurate due to the fact that a local hysteresis loop described by a unified inverse J-A model is not closed. The method comprises the following steps: acquiring a magnetic flux density sequence and hysteresis loop data; calculating the magnetic field intensity corresponding to the flux density on the main hysteresis loop by using an inverse J-A model, finding a first local turning point, finding a revolution curve closest to the first local turning point, finding a second local turning point, performing revolution symmetry on the revolution curve, modeling the revolution curve based on an inverse hyperbolic sine function, and calculating the magnetic field intensity corresponding to the flux density on the main hysteresis loop. Calculating the magnetic field intensity corresponding to the flux density on the revolution curve through the model; hysteresis loss is determined according to the magnetic flux density and the magnetic field intensity, and then core loss is determined according to the hysteresis loss. The method is used for calculating the iron core loss.

Description

technical field [0001] The invention belongs to the field of iron loss calculation, in particular to an iron loss calculation method based on local hysteresis loop modeling. Background technique [0002] With the development of my country's economy, the increasing demand for power consumption has prompted the rapid advancement of power grid construction, and more and more transformers and smoothing reactors have been put into use in the power grid. Transformers and smoothing reactors are the main equipment of the power transmission and transformation system, and the iron core is its key component. Core loss has an important impact on the heating and insulation of transformers and smoothing reactors, and is an important reference standard for design. The iron core is mainly composed of ferromagnetic materials. The magnetization and loss of ferromagnetic materials have nonlinear characteristics. At the same time, due to the extensive use of power electronic equipment such as ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/23G06F17/13G06F17/18
CPCY02E60/00
Inventor 陈磊蔡唯世柴凤裴宇龙于艳君
Owner HARBIN INST OF TECH
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com