Systems and methods for determining optimal parameters for dynamic quantum clustering analyses

a dynamic quantum and clustering analysis technology, applied in the field of data clustering, can solve the problems of data clustering that is often ill-defined in a mathematical sense, the performance of this quantum clustering approach can have an undetectable high sensitivity to the value of the quantum clustering scale parameter, and achieve the effect of reducing the dimensionality of the set of source data

Active Publication Date: 2019-01-01
THE BOARD OF TRUSTEES OF THE LELAND STANFORD JUNIOR UNIV +1
View PDF17 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

[0015]In yet another additional embodiment of the invention, the method further includes preprocessing the set of source data points to reduce the dimensionality of the set of source data using the dynamic quantum clustering server system.

Problems solved by technology

Clustering of data is a well-known problem of pattern recognition.
In general, data clustering is often ill-defined in a mathematical sense.
Nonetheless, it is a very important problem in many scientific and technological fields of study.
In some cases, the performance of this quantum clustering approach can have an undesirably high sensitivity to the value of the quantum clustering scale parameter.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Systems and methods for determining optimal parameters for dynamic quantum clustering analyses
  • Systems and methods for determining optimal parameters for dynamic quantum clustering analyses
  • Systems and methods for determining optimal parameters for dynamic quantum clustering analyses

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

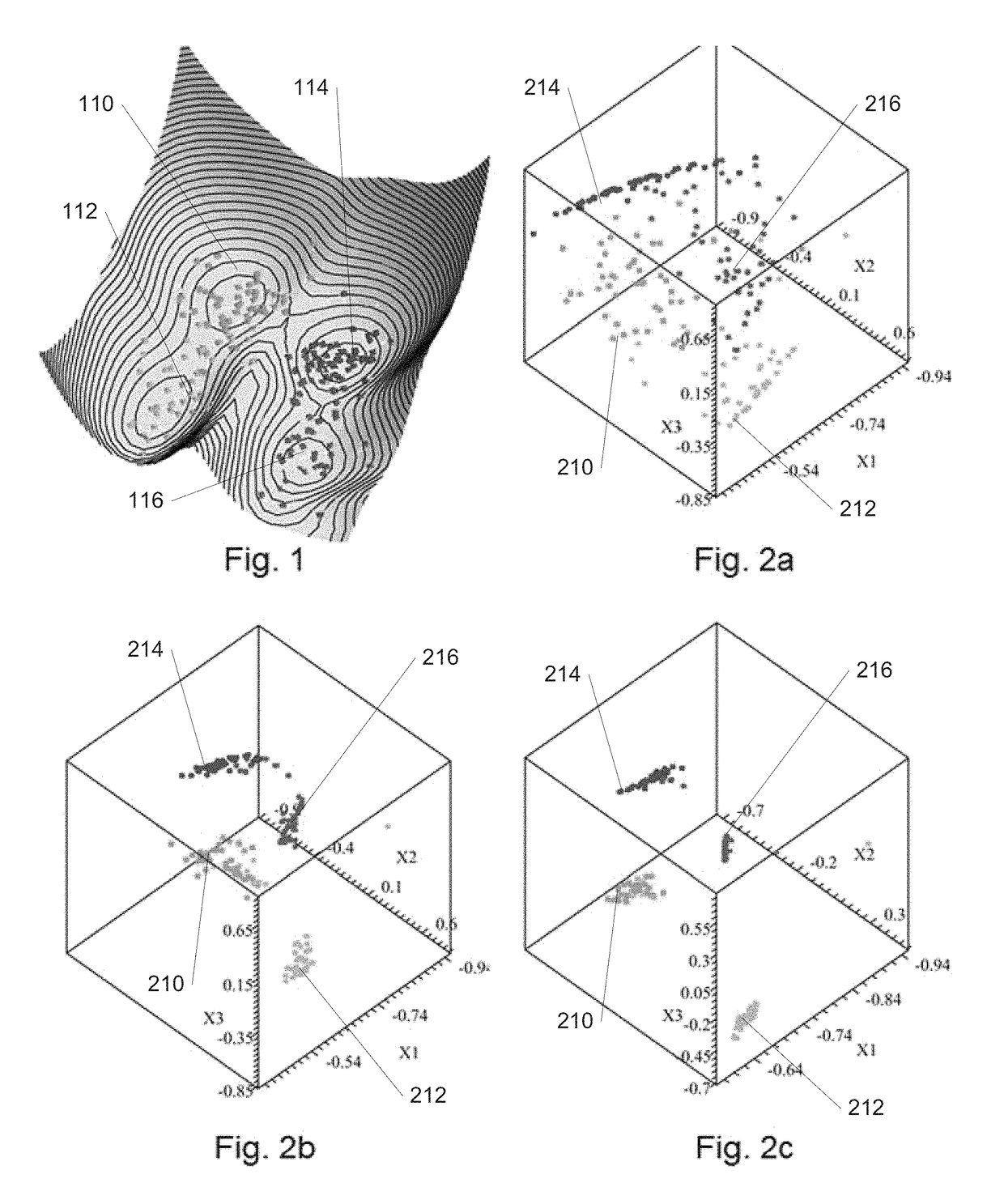
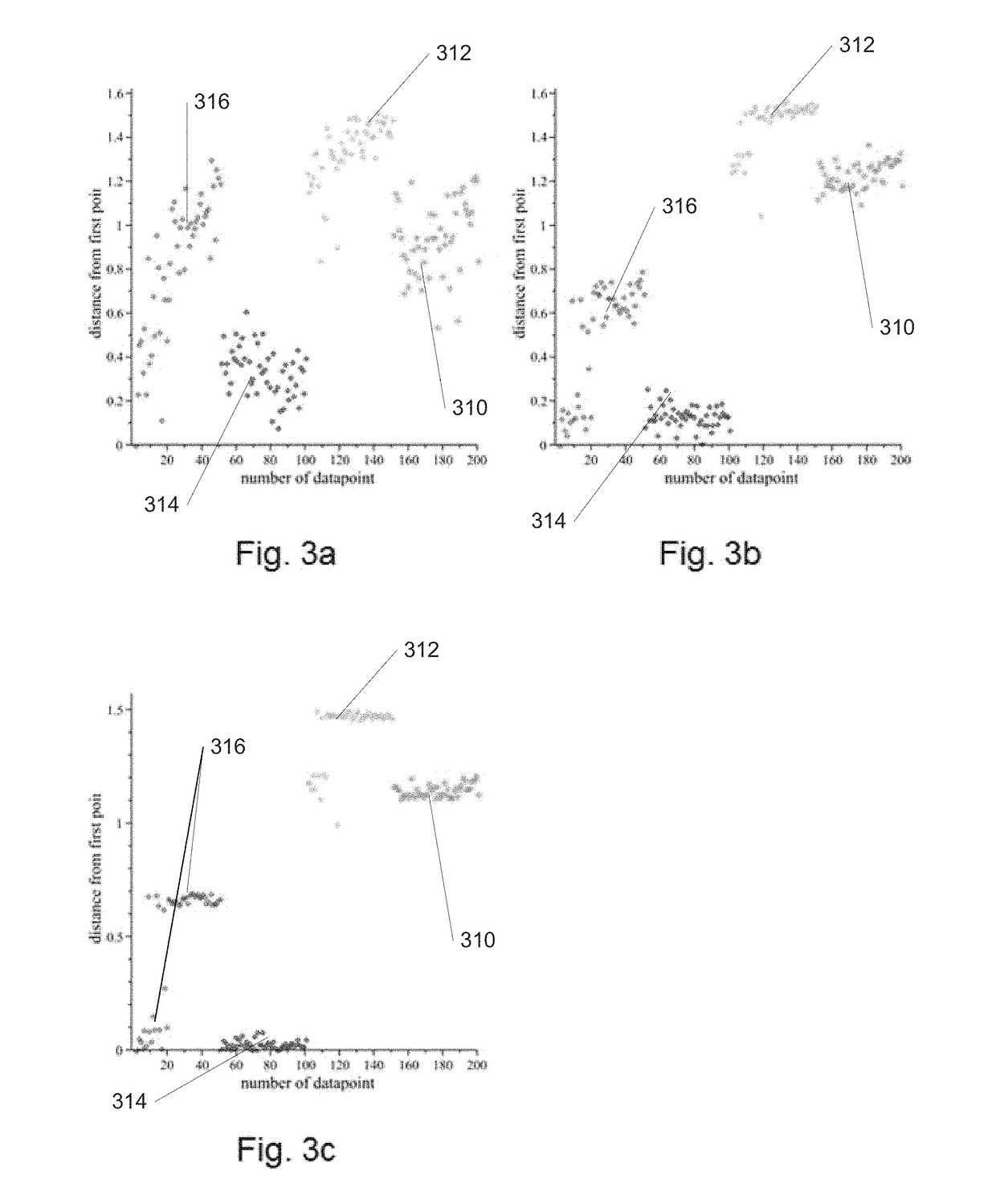
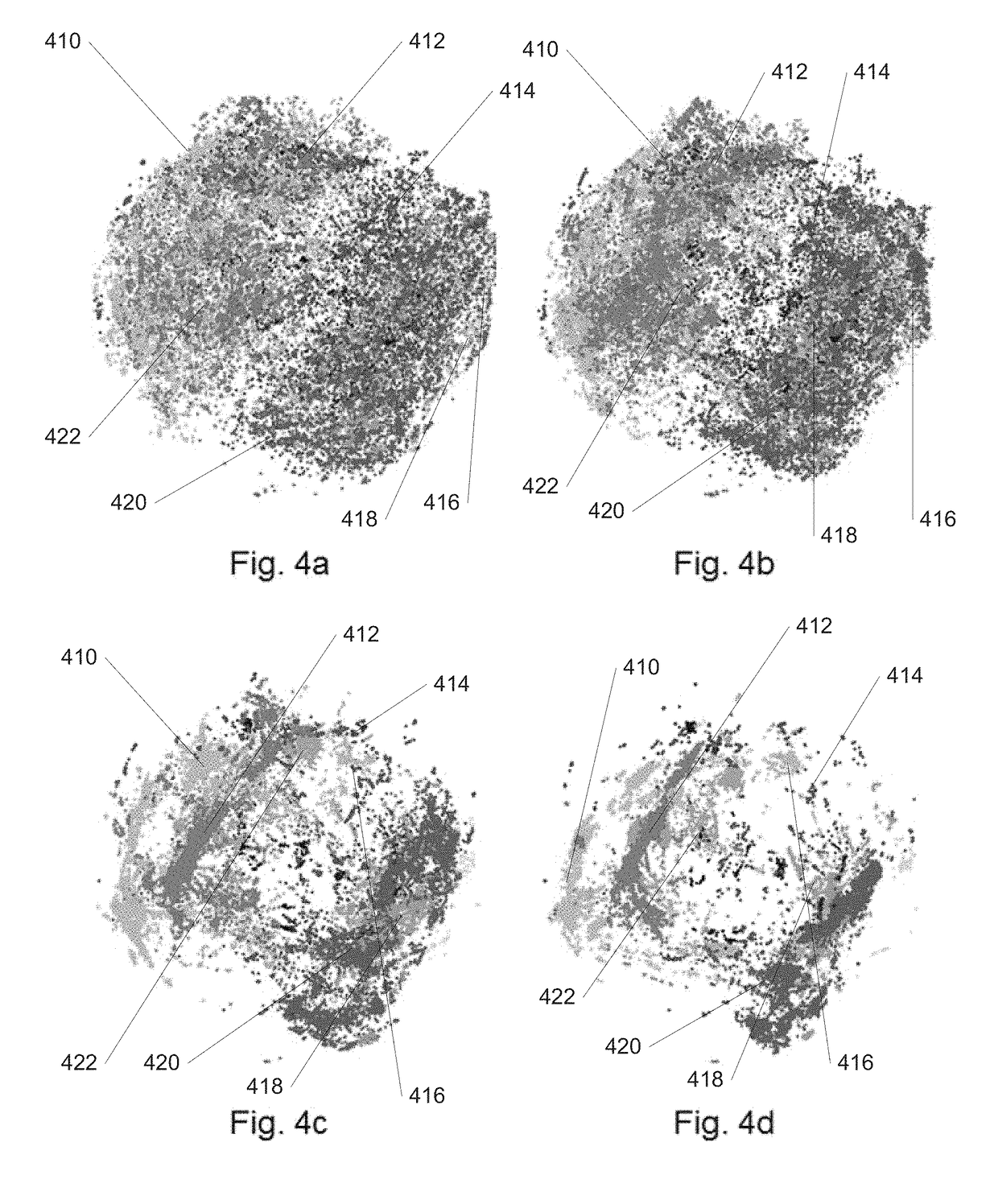
[0055]Turning now to the drawings, systems and methods for dynamic quantum clustering in accordance with embodiments of the invention are described. Dynamic quantum clustering (DQC) can be flexibly applied to datasets that present significantly different challenges, we also show how a simple analysis can be used to look for the needle in the haystack, determine what it is, and find what this means. In this work, we advocate the use of a Schrödinger Hamiltonian Ĥ that is intimately connected to the data-structure, as defined by the quantum clustering method summarized below. We extend it into a time-dependent Schrödinger equation:

[0056]i⁢∂ψ⁡(x→,t)∂t=H^⁢⁢ψ⁡(x→,t)(2)

The ensuing DQC formalism allows us, by varying a few parameters, to study in detail the temporal evolution of wave-functions representing the original data points. In turn, this dynamical behavior allows us to explore the structure of the quantum potential function defined by the quantum clustering method.

[0057]DQC begins ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

In the present work, quantum clustering is extended to provide a dynamical approach for data clustering using a time-dependent Schrödinger equation. To expedite computations, we can approximate the time-dependent Hamiltonian formalism by a truncated calculation within a set of Gaussian wave-functions (coherent states) centered around the original points. This allows for analytic evaluation of the time evolution of all such states, opening up the possibility of exploration of relationships among data points through observation of varying dynamical-distances among points and convergence of points into clusters. This formalism may be further supplemented by preprocessing, such as dimensional reduction through singular value decomposition and / or feature filtering. Additionally, the parameters of the analysis can be modified in order to improve the efficiency of the dynamic quantum clustering processes.

Description

CROSS REFERENCE TO RELATED APPLICATIONS[0001]This application claims priority to U.S. Provisional Patent Application No. 61 / 881,399, filed Sep. 23, 2013 and titled “Visually Exploring Large, Complex Datasets for Hidden Structure” and is a continuation-in-part of U.S. patent application Ser. No. 14 / 482,961, filed Sep. 10, 2014, which is a continuation of U.S. patent application Ser. No. 12 / 586,036, filed Sep. 15, 2009, which claims the benefit of U.S. Provisional Patent Application No. 61 / 198,621, filed Nov. 7, 2008 and titled “Method for Discovering Relationships in Data by Dynamic Quantum Clustering”, the disclosures of which are hereby incorporated by reference in their entirety.GOVERNMENT SPONSORSHIP[0002]This invention was made with US government support under contract number DE-AC02-765F00515 awarded by the Department of Energy. The government has certain rights in this invention.FIELD OF THE INVENTION[0003]This invention relates to data clustering and more specifically to time...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
Patent Type & Authority Patents(United States)
IPC IPC(8): G06F7/60G06K9/62
CPCG06F17/30601G06K9/6247G06K9/622G06F16/287G06V10/763G06F18/232G06F18/2135
Inventor WEINSTEIN, MARVINHORN, DAVID
Owner THE BOARD OF TRUSTEES OF THE LELAND STANFORD JUNIOR UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap