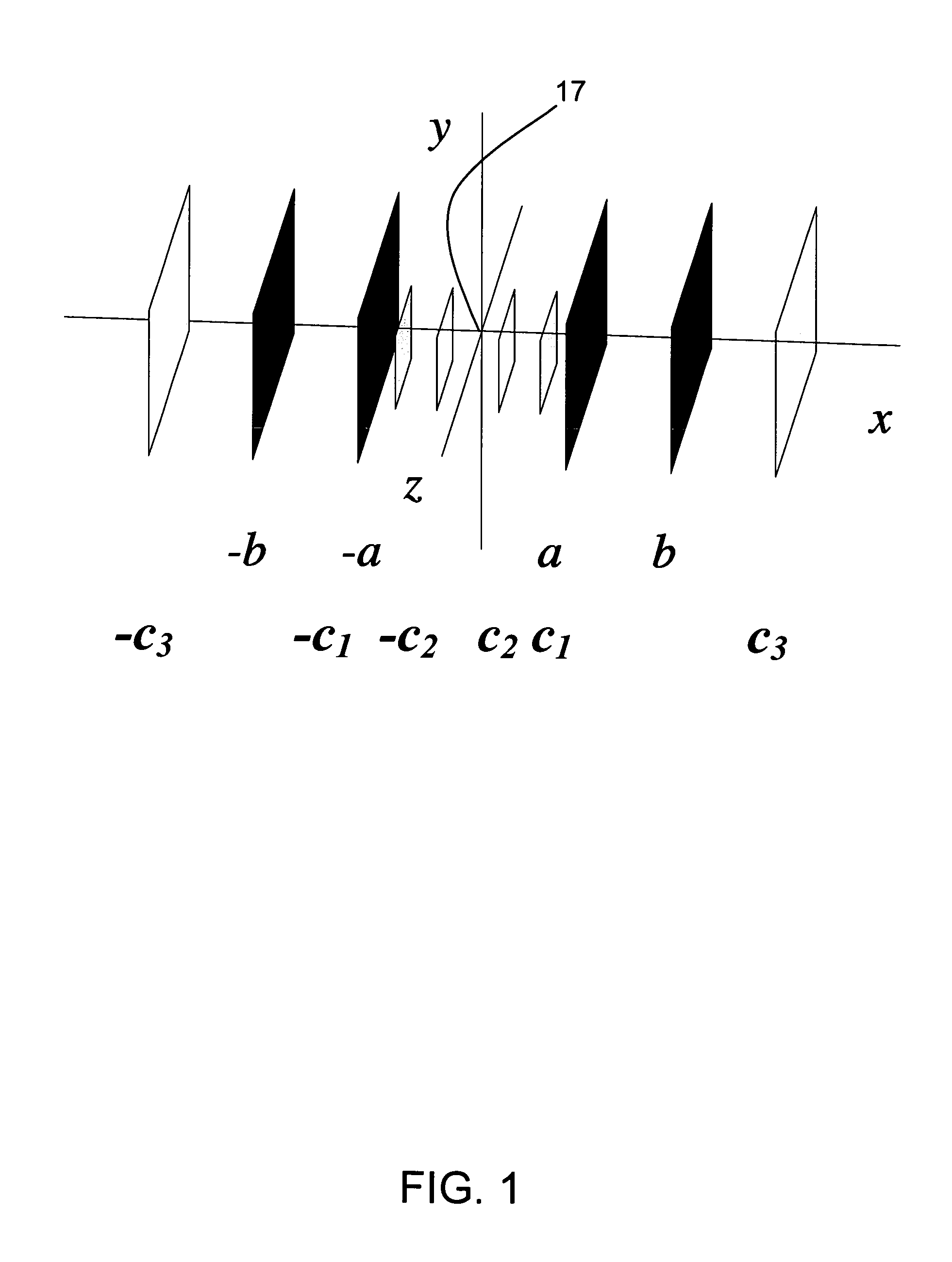Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Bi-planar coil assemblies for producing specified magnetic fields

a technology of biplanar coils and magnetic fields, applied in the direction of instruments, using reradiation, diagnostic recording/measuring, etc., can solve the problems of inability to yield a solution, affecting the design of complex magnetic fields, and affecting the quality of governing equations, etc., to achieve the effect of reducing the magnitude of the magnetic field

Inactive Publication Date: 2007-03-20
THE UNIV OF QUEENSLAND +1
View PDF19 Cites 10 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

[0031]The procedures outlined in steps (1) and (2) above can be preferably used for multiple target regions including an external field normally set to zero for the purposes of actively shielding the coil set (i.e., reducing the stray field outside the coils).
[0074](3) the third and fourth coils are shielding coils that serve to reduce the magnitude of the magnetic field produced by the bi-planar coil assembly outside of the third and fourth coil assemblies (e.g., the magnitude of the magnetic field outside of the planes x=±c3 in FIG. 1).

Problems solved by technology

On the other hand, it is possible that complicated magnetic fields (with tesseral components, for example) may be difficult to design by this method, particularly in view of the number of numerical iterations required in the simulated annealing technique.
As expected, the governing equations are so ill-conditioned as to be incapable of yielding a solution in the usual sense; however, this difficulty is overcome using a regularization approach similar to the Tikhonov method (see, for example, Delves and Mohamed, Computational Methods for Integral Equations, Cambridge University Press, Cambridge 1985, page 307).

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Bi-planar coil assemblies for producing specified magnetic fields
  • Bi-planar coil assemblies for producing specified magnetic fields
  • Bi-planar coil assemblies for producing specified magnetic fields

Examples

Experimental program
Comparison scheme
Effect test

example 1

5.1 Example 1

[0191]The T00 (Constant Field) Bi-pChecklanar Coil

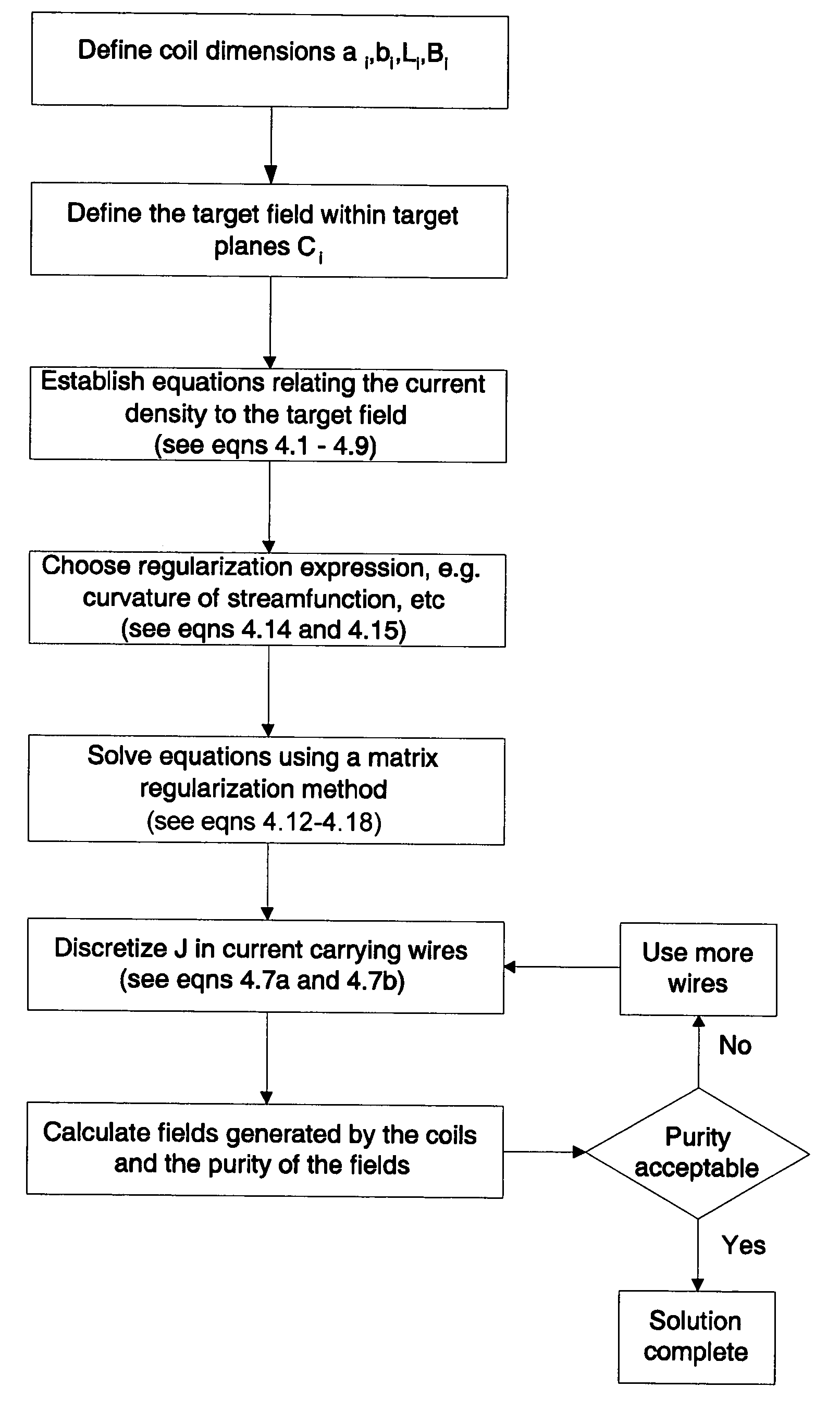
[0192]In this example, the method of the invention is used to design shielded and unshielded bi-planar coils that are intended to produce symmetrically located T00 fields within the primary bi-planar coil. For this coil, the target fields are simply constants, and so HX is simply a constant on each of the three pairs of target planes. We therefore set

HTX(c1;y,z)=Hmax

HTX(c2;y,z)=Hmax

HTX(c3;y,z)=0.  (5.2)

Here, the constant transverse magnetic field within the primary coils has been assumed to take the value Hmax=1 amp / meter. The target field at x=±c3 is set to zero, reflecting the intended function of the shields. Since the T00 field is even in the x-coordinate (it is constant), the primary coil windings on the plane at x=−a are in phase with those on x=a, and the same is true for the shields on the planes x=±b. (This even target field requires the last term in equation (4.11) to take a plus sign).

[0193]To begin, the cas...

example 2

5.2 Example 2

[0201]The T11 Bi-planar Coil

[0202]As a further illustration of the use of this invention, shielded bi-planar coils will be designed in this section, both for symmetric and asymmetrically located T11 fields. The transverse magnetic field component for this case has the general form HX(x,y,z)=C11x with C11 an arbitrary constant. It follows that the target fields on the three pairs of target planes used in this invention must be given by the equations

[0203]HTX⁡(c1;y,z)=Hmax⁡(c1a)⁢⁢HTX⁡(c2;y,z)=Hmax⁡(c2a)⁢⁢HTX⁡(c3;y,z)=0.(5.3)

Here, the constant Hmax is now the maximum magnetic field strength (in the x-component) on the plane x=a of the primary coil. Its value is set to 1 amp / meter here, for illustrative purposes. As this target field is now anti-symmetric in x, it follows that the coils on the opposing planes of the bi-planar coil (and also the shields) are counter-wound. This is the case discussed explicitly in Section 4.3.

[0204]The primary winding for a shielded T11 coil ...

example 3

5.3 Example 3

[0211]The T21 Bi-planar Coil

[0212]Another illustration of the use of this invention concerns the design of shielded bi-planar T21 coils. The technique has been used to design both symmetric and asymmetrically located fields, although only the latter case will be discussed here.

[0213]The transverse component for a symmetrically located T21 magnetic field has the general form HX(x,y,z)=3C21xz, where C21 is again an arbitrary constant. For a field that is asymmetrically positioned with respect to the origin, it therefore follows that the target fields take the forms

[0214]HTX⁡(c1;y,z)=Hmax⁡(2⁢c1a)⁢Z2(q-p)HTX⁡(c2;y,z)=Hmax⁡(2⁢c2a)⁢Z2(q-p)HTX⁡(c3;y,z)=0.(5.4)

[0215]Again, the constant Hmax is set to the value 1 amp / meter here, for illustrative purposes. This field (5.4) is also anti-symmetric in x, as for the case discussed in Section 5.2, and so the coils on the opposing planes of the bi-planar coil and shield are also counter-wound. The quantity Z2 in equations (5.4) is the ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

Bi-planar coil assemblies are disclosed which have DSV's whose centers are offset by distances D from the origins of x,y,z-coordinate systems, where said origins of x,y,z-coordinate systems are coincident with the geometric centers of the coils. The distances D can be of the order of 10-20 centimeters or more. The bi-planar coil assemblies can be used in MRI applications to reduce the feeling of claustrophobia experienced by some subjects. The assemblies also can facilitate the imaging of various joints, including the wrist, elbow, ankle, or knee.

Description

FIELD OF THE INVENTION[0001]This invention relates to bi-planar coils for producing desired (specified) magnetic fields, and to certain preferred methods for designing such coils.[0002]The coils of this invention are particularly suitable for use in magnetic resonance imaging (MRI) equipment. In that application, bi-planar coils enable high-resolution medical imaging to be performed in a manner that reduces the claustrophobia experienced by many patients, and also allows access by medical specialists. However, the application of the present invention is by no means restricted to MRI technology, and is available in any equipment for which parallel plates might be used to generate a desired magnetic field, e.g., a desired stationary magnetic field. Thus it is envisaged that the present invention may also find application in the design of wiggler magnets in synchrotron technology (see, for example, R. A. Cover, G. Rakowsky, B. L. Bobbs and P. K. Kennedy, 1995, Undulator design for sync...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(United States)
IPC IPC(8): G01V3/00A61B5/055G01R33/385G01R33/38
CPCG01R33/3806G01R33/381G01R33/3815
Inventor FORBES, LAWRENCE KENNEDYCROZIER, STUART
Owner THE UNIV OF QUEENSLAND
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com