Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimization method for detecting and positioning by detecting instrument

A technology of detecting instruments and optimization methods, which is applied in the field of graphics, can solve problems such as the rapid increase in the number of detecting instruments, and achieve the effect of increasing the number

Inactive Publication Date: 2011-04-20
FUDAN UNIV
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

And the prior art detects once every time, and the position of detection instrument is uncertain, and needs to adjust new position according to the data that detects; When the number of vertices of the object is large, the number of detection instruments will increase rapidly

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimization method for detecting and positioning by detecting instrument
  • Optimization method for detecting and positioning by detecting instrument
  • Optimization method for detecting and positioning by detecting instrument

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

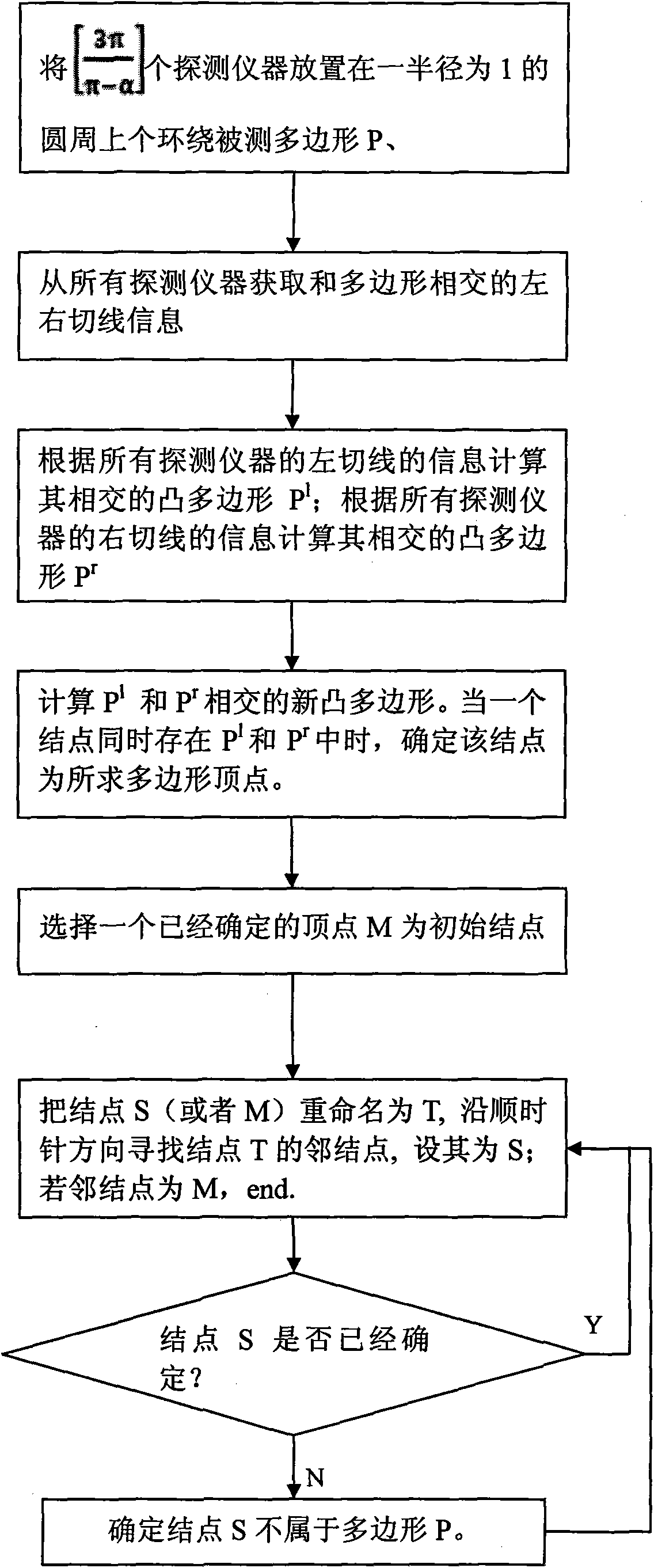
[0058] Example 1. Reconstruction of polygons in two dimensions

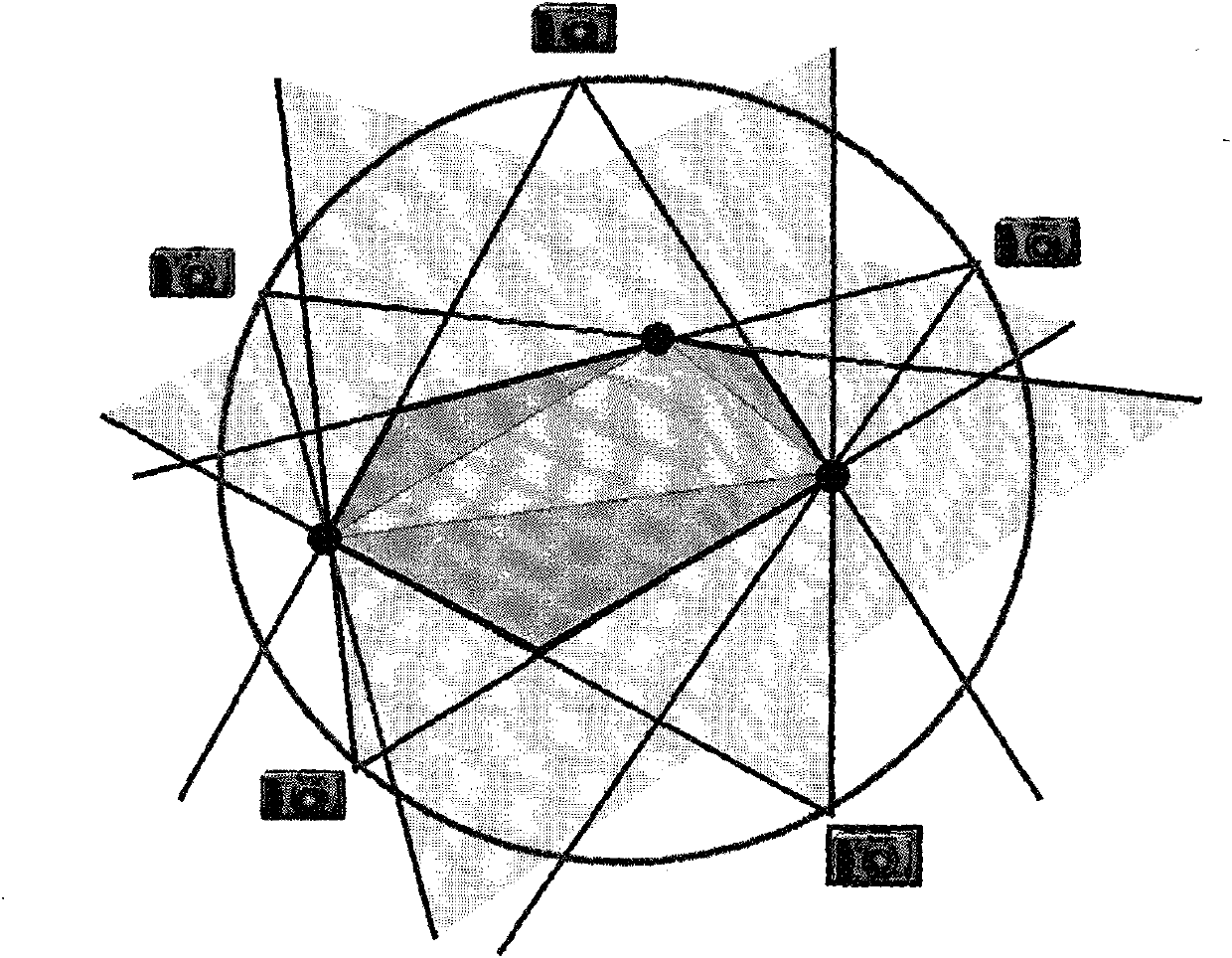
[0059] In the two-dimensional case, such as image 3 As shown, the method in which all cameras are evenly placed on the circumference is optimal.

[0060] Suppose there are K cameras placed on the circumference, M={C 0 , C 1 ,...,C K-1} is the position of the camera in the clockwise direction. Then any camera C i to C i+3 The arc distance along the circumference must be ≤ 2(π-α). Suppose there exists a j such that C j to C j+3 The distance is 2(π-α)+ε, ε>0, then it can be in C i with C i+1 Find an arc length dist(C i , C i+1 )-ε / 2, where dist(C i , C i+1 ) for C i to C i+1 arc distance. The same can be done in C i+1 with C i+3 Find an arc length dist(C i+1 , C i+3 )-ε / 2, the sum of these two arc lengths is:

[0061] dist(C i , C i+1 )-ε / 2+dist(C i+1 , C i+3 )-ε / 2=dist(C i , C i+3 )-ε=2(π-α)

[0062] then there may be a polygon placement location such as Figure 5 As shown, the maximu...

Embodiment 2

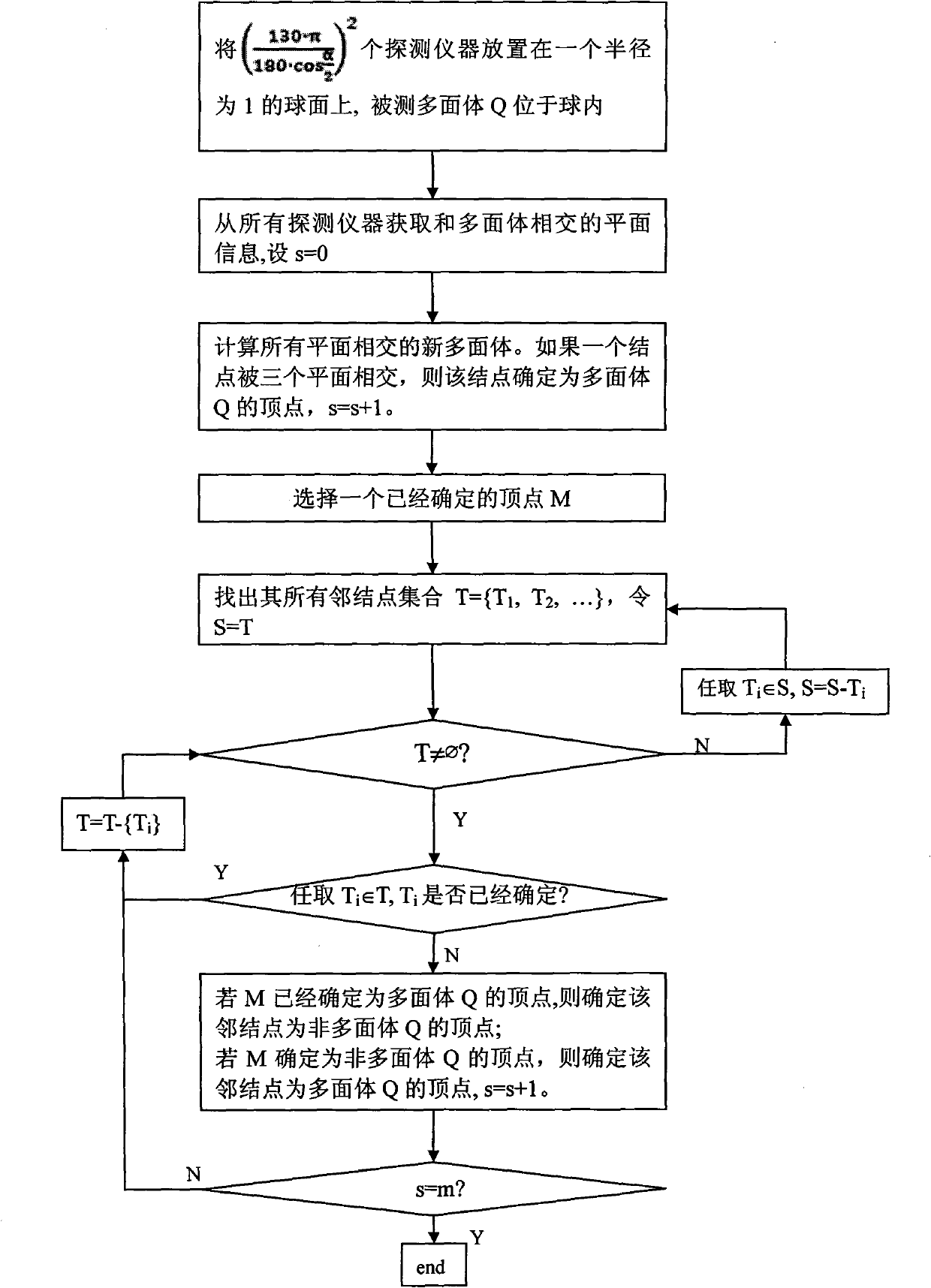
[0081] Example 2. Reconstruction of polyhedra in three dimensions

[0082] In the three-dimensional case, assuming that all cameras are placed on a spherical surface with a radius of 1, the polyhedron Q we want to reconstruct can be in any direction, located at any position within the sphere, and the maximum face angle of the polyhedron Q does not exceed α. Similarly, each camera can obtain multiple rays tangent to multiple vertices of the polyhedron, and these rays form a polyhedral cone with the camera position as the vertex (see Figure 4 ), several edges of the cone are respectively tangent to several vertices of the polyhedron Q. Therefore, in the three-dimensional case, each vertex of the polyhedron Q needs to be detected by at least two cameras, and we can obtain the position information of the vertex through the intersection of the two tangents detected by the cameras.

[0083] Assume that v is any vertex intersected by N (≥ 3) faces in polyhedron Q, and all face angl...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the technical field of graphics, and relates to an optimization method for detecting and positioning by a detecting instrument. A plane and spatial point positioning principle is applied, the fewest one group of detecting instrument is configured to detect a given two-dimensional polygon or three-dimensional polyhedron to be detected from different angles to acquire tangent information of the polygon or the polyhedron so as to reconstruct the specific position and shape of the polygon or the polyhedron. By the optimization method, the number of the optimized or fewest detecting instrument required by the detection is only related to the maximum interior angle of the polygon or the face angle of the maximum face of the polyhedron; and once the number of required tactile sensors is determined, the positions of the tactile sensors can be permanently fixed.

Description

technical field [0001] The invention belongs to the technical field of graphics and relates to an optimization method for detection and positioning of detection instruments. Background technique [0002] The main research of geometric detection method is to determine or confirm the structure or properties of an object (such as shape, position, etc.) through detection results. Cole and Yap proposed the earliest geometric detection method from the problem of robot research - finger detection finger probe. This method mainly obtains the information of the first intersection point of a straight line and the object to be measured by detection, and the information of these intersection points is obtained. Reconstruct the object to be tested; in some confirmation methods such as the "shape-based model-based problem" method, the shape of the object to be tested is known, but the specific orientation or position is unknown. This method mainly It is to study at least how many detecti...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01B11/00G01B11/24
Inventor 鲁道夫王怡慧
Owner FUDAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com