Parallel algorithm of computing convex hull based on multinuclear framework
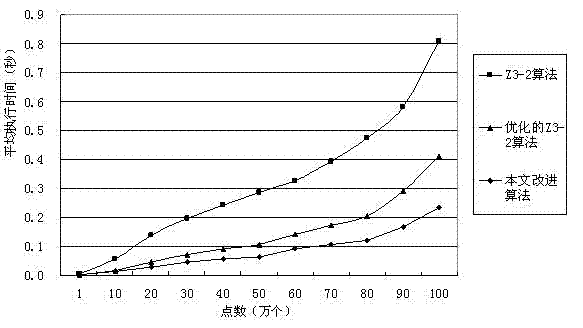
A parallel algorithm and convex hull technology, applied in the field of computational geometry, can solve the problems of occupying computing resources and cumbersome algorithms, and achieve the effects of saving computing resources, eliminating bottlenecks, and reducing parallel overhead
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0034]The technical solutions provided by the present invention will be described in detail below in conjunction with specific examples. It should be understood that the following specific embodiments are only used to illustrate the present invention and are not intended to limit the scope of the present invention.
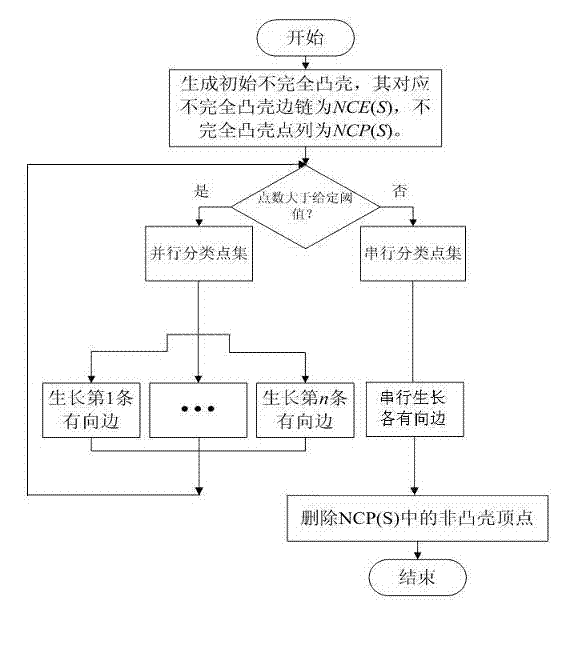
[0035] The parallel algorithm flow of calculating the convex hull based on the multi-core architecture is as follows: figure 1 As shown, the specific process is described as follows:
[0036] (1) First find the initial incomplete convex hull of the initial point set, and its sides are represented by directed edges in the counterclockwise direction: find four extreme points along the x-coordinate and y-coordinate directions, and delete the same , the convex polygon surrounded by the remaining points in the counterclockwise direction is the initial incomplete convex hull, denoted as LPBCH(S).
[0037] LPBCH(S) includes NCP(S) and NCE(S); the vertex column in the in...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com