Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Electric system low-frequency oscillation mode parameter identification method

A low-frequency oscillation and power system technology, applied in the direction of reducing/preventing power oscillation, etc., can solve the problems of weak anti-noise and poor identification accuracy, and achieve the effect of strong anti-noise and high identification accuracy

Active Publication Date: 2014-12-24
STATE GRID CORP OF CHINA +2
View PDF2 Cites 34 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] The invention provides a method for identifying parameters of a low-frequency oscillation mode of a power system, which solves the technical problems of weak anti-noise and poor identification accuracy in the existing method for identifying parameters of a low-frequency oscillation mode of a power system based on random response signals, and realizes The method of parameter identification method for low-frequency oscillation mode of power system based on random response signal has strong noise immunity and high identification accuracy.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Electric system low-frequency oscillation mode parameter identification method
  • Electric system low-frequency oscillation mode parameter identification method
  • Electric system low-frequency oscillation mode parameter identification method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

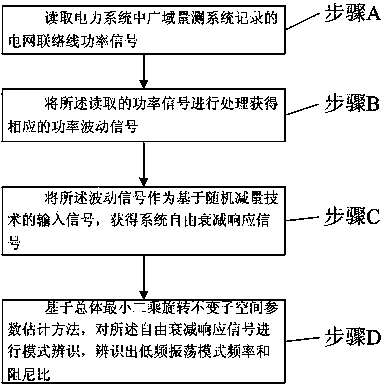
[0050] In Embodiment 1, a method for identifying parameters of a power system low-frequency oscillation mode is provided. Please refer to Figure 1-Figure 2 , the method includes:

[0051] Step A: Read the grid tie line power signal recorded by the wide area measurement system in the power system;

[0052] Step B: Process the read power signal to obtain a corresponding power fluctuation signal;

[0053] Step C: using the fluctuating signal as an input signal based on a random decrement technique to obtain a system free attenuation response signal;

[0054] Step D: Based on the overall least squares rotation invariant subspace parameter estimation method, perform mode identification on the free decay response signal, and identify the low frequency oscillation mode frequency and damping ratio.

[0055] Wherein, in the embodiment of the present application, the processing of the read power signal to obtain the corresponding power fluctuation signal is specifically:

[0056] Th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an electric system low-frequency oscillation mode parameter identification method. The method includes the steps that firstly, interconnecting tie power signals recorded by a wide-area measuring system in an electric system are read; the read power signals are processed, and then corresponding power fluctuation signals are acquired; then the fluctuation signals serve as input signals based on the random decrement technology, and free attenuation response signals of the system are acquired; finally, based on a total least square rotation invariant sub-space parameter estimation method, mode identification is conducted on the free attenuation response signals, low-frequency oscillation mode frequency and the damping ratio are identified, and the electric system low-frequency oscillation mode parameter identification method based on the random response signals has the technical advantages of being high in noise immunity and identification accuracy.

Description

technical field [0001] The invention relates to the field of power system information processing, in particular to a method for identifying parameters of a low-frequency oscillation mode of a power system. Background technique [0002] With the improvement of power system interconnection, continuous expansion of scale, and the extensive use of fast excitation systems, the problem of low-frequency oscillation has become more and more prominent, and has become a bottleneck that threatens system stability and limits the transmission capacity of interconnected power grids. Discovering and accurately grasping the low-frequency oscillation mode parameters of the system is of great significance to the safe and stable operation of the power system. [0003] The phasor measurement unit (PMU) of the wide area measurement system (WAMS) can quickly and synchronously record the time response curve of the wide area distribution, truly reflect the dynamic behavior of the power system, and ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H02J3/24
Inventor 汤凡王祥超王晓茹张鹏滕予非
Owner STATE GRID CORP OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com