Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Non-stationary random dynamic response analysis method considering geometric nonlinearity of structure

A geometric nonlinear and response analysis technology, applied in special data processing applications, instruments, electrical digital data processing, etc., to achieve the effect of solving non-stationary random dynamic response analysis

Inactive Publication Date: 2016-11-09
SOUTHEAST UNIV
View PDF2 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] Purpose of the invention: The present invention provides a non-stationary random dynamic response analysis method considering the geometric nonlinearity of the structure, which solves the limitation that the cur

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Non-stationary random dynamic response analysis method considering geometric nonlinearity of structure
  • Non-stationary random dynamic response analysis method considering geometric nonlinearity of structure
  • Non-stationary random dynamic response analysis method considering geometric nonlinearity of structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

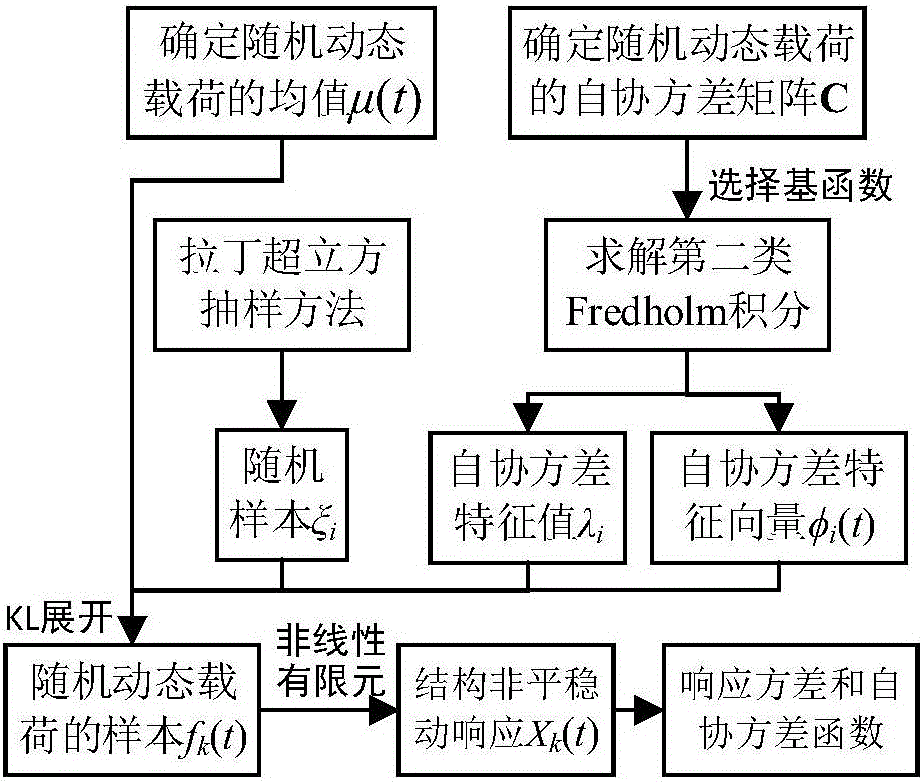
[0035] like figure 1 As shown, this embodiment specifically includes the following steps:

[0036] (1) Calculate the mean value and autocovariance matrix according to the non-stationary random dynamic load.

[0037] Among them, the mean of the non-stationary random dynamic load F(t) is: μ(t)=E[F(t)]; the autocovariance matrix is: C(t 1 ,t 2 )=E[(F(t 1 )-μ(t 1 ))(F(t 2 )-μ(t 2 ))]; where, t 1 , t 2 is a time variable, and E[·] means to seek the expected value.

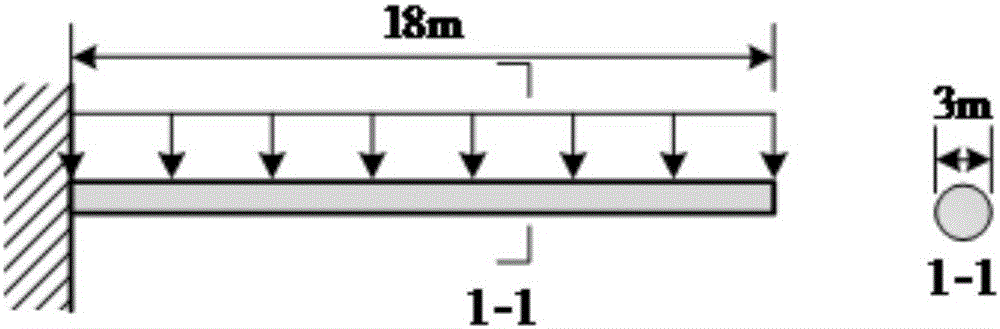
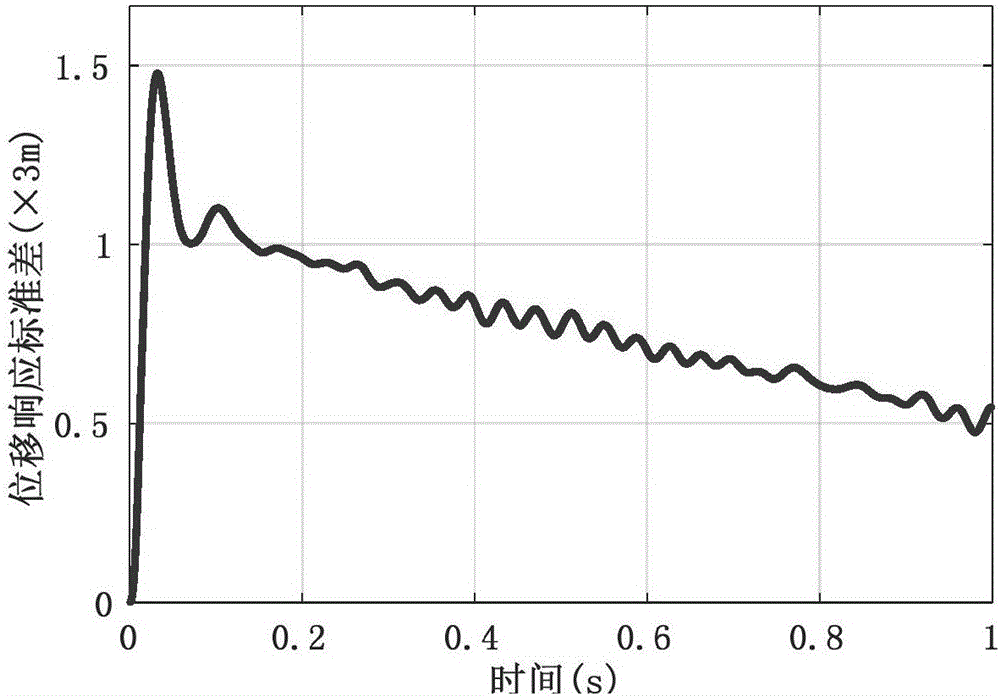
[0038] Taking a cantilever beam structure as the research object (such as figure 2 shown), and its geometric parameters and material parameters are shown in Table 1. The mean value is zero, the autocovariance is a random uniformly distributed random dynamic load in the form of modulation index, the number of load steps is 1000, and the load duration is 1s. Then the mean value of the random dynamic load is μ(t)=0, and the autocovariance matrix is:

[0039] Table 1 Material parameters of the cantilever beam...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a non-stationary random dynamic response analysis method considering geometric nonlinearity of a structure. The method comprises the steps of (1) performing calculation according to non-stationary random dynamic loads to obtain a mean value and an auto-covariance matrix of the loads; (2) calculating an eigenvalue and an eigenvector of the auto-covariance matrix, and obtaining truncation orders of the eigenvalue and the eigenvector; (3) decomposing the non-stationary random dynamic loads based on KL expansion and Latin hypercube sampling methods to obtain a group of random samples of the non-stationary random dynamic loads; and (4) establishing a finite element model of the structure, calculating the random samples of the non-stationary random dynamic loads as response functions of the loads by adopting a transient analysis method, and performing calculation according to the response functions to obtain variance and auto-covariance functions. According to the method, the limitation of conventional non-stationary random dynamic response analysis only for a linear structure is overcome.

Description

technical field [0001] The invention relates to a non-stationary random dynamic response analysis method, in particular to a non-stationary random dynamic response analysis method considering structural geometric nonlinearity. Background technique [0002] Engineering structures may be subjected to stationary or non-stationary random dynamic loads during actual service, such as gust loads, turbulent boundary layer loads, wind loads, and earthquake loads. However, in practical applications, due to the limitations of non-stationary random dynamic response analysis methods, non-stationary random dynamic loads are often simplified into stationary random dynamic loads. error. Therefore, it is necessary to consider the non-stationary characteristics of loads in random dynamic response analysis. [0003] At present, for the dynamic response analysis under non-stationary random excitation, the random dynamic load is often decomposed into a series of deterministic random variables ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCG06F30/23
Inventor 李彦斌费庆国吴邵庆廖涛张鹏
Owner SOUTHEAST UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com