Supercharge Your Innovation With Domain-Expert AI Agents!

Multi-target tracking method and system for flicker noise

A multi-target tracking and flicker noise technology, which is applied in the field of multi-target tracking methods and systems to solve tracking problems and improve tracking accuracy.

Inactive Publication Date: 2017-05-31
SHENZHEN UNIV
View PDF5 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The technical problem to be solved by the present invention is to provide a multi-target tracking method and tracking system suitable for flicker noise, aiming at solving the problem of tracking nonlinear moving targets under flicker noise

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-target tracking method and system for flicker noise
  • Multi-target tracking method and system for flicker noise
  • Multi-target tracking method and system for flicker noise

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

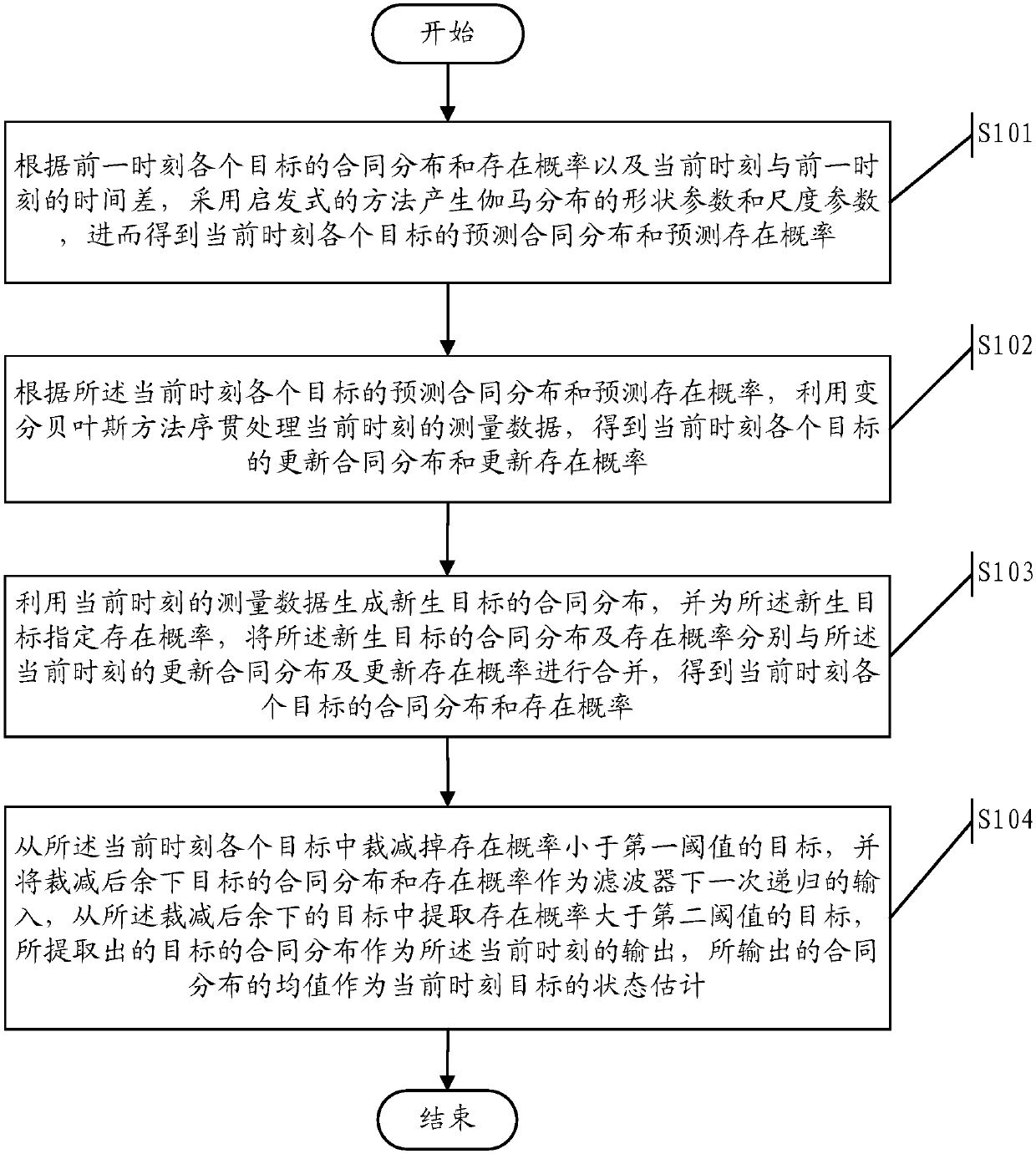
[0021] In order to make the object, technical solution and advantages of the present invention clearer, the present invention will be further described in detail below in conjunction with the accompanying drawings and embodiments. It should be understood that the specific embodiments described here are only used to explain the present invention, not to limit the present invention.

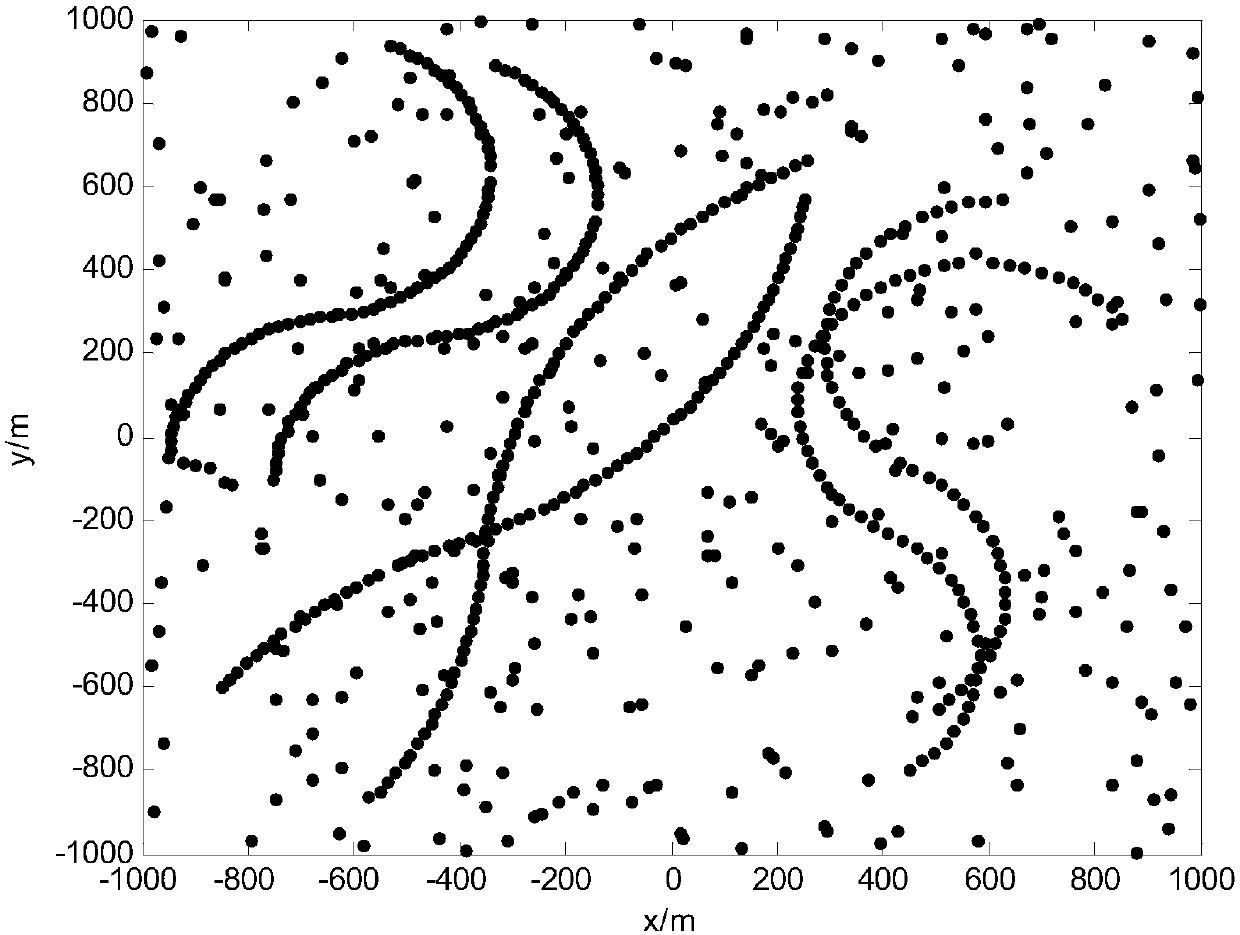
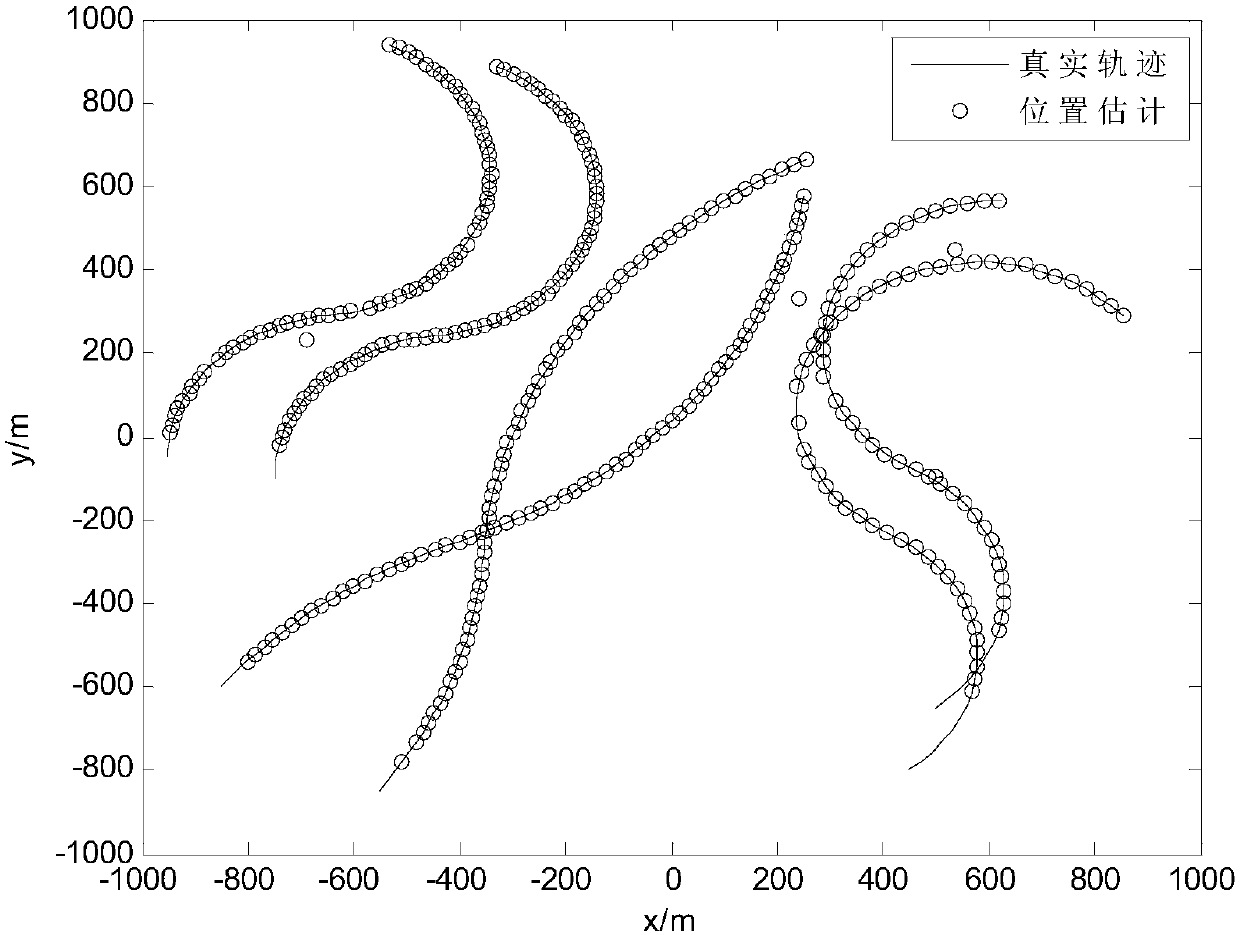
[0022] According to the contract distribution and existence probability of each target of the measurement data received at the previous moment, the embodiment of the present invention predicts the contract distribution and existence probability of each target of the new measurement data received at the current moment; according to the predicted contract distribution and existence probability, use The variational Bayesian method sequentially processes each measurement at the current moment to obtain the updated contract distribution and existence probability of each target; respectively merges the up...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention is applicable to the field of multi-sensor information fusion and provides a multi-target tracking method and system for flicker noise. The method comprises a prediction step, an updating step, a generation step and an extraction step. According to the technical scheme provided by the invention, while the real-time performance of data processing is guaranteed, a tracking problem of a nonlinear moving target under flashing noise is solved effectively.

Description

technical field [0001] The invention belongs to the technical field of multi-sensor information fusion, and in particular relates to a multi-target tracking method and system suitable for flicker noise. Background technique [0002] Edge distribution Bayesian filter is an effective method for multi-target tracking under clutter and noise, but the filter is only suitable for the case of Gaussian noise, not flicker noise. How to solve the multi-target tracking problem under flicker noise is a key technical problem that needs to be explored and solved. Contents of the invention [0003] The technical problem to be solved by the present invention is to provide a multi-target tracking method and tracking system suitable for flicker noise, aiming at solving the problem of tracking nonlinear moving targets under flicker noise. [0004] The present invention is achieved in that a kind of multi-target tracking method applicable to flicker noise comprises: [0005] According to th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01S13/66
CPCG01S13/66
Inventor 刘宗香邹燕妮谢维信李良群
Owner SHENZHEN UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com