Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Spacecraft attitude-track integrated backstepping tracking control method

A tracking control and spacecraft technology, applied in attitude control, three-dimensional position/channel control, etc., can solve problems such as poor tracking effect, and achieve the effect of great practical application engineering value

Active Publication Date: 2017-06-09
黑龙江省工研院资产经营管理有限公司
View PDF2 Cites 32 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0059] The purpose of the present invention is to solve the shortcomings of poor tracking effect caused by independent control methods for the orbit and attitude of the spacecraft in the prior art, and propose an integrated backstepping tracking control method for the attitude and orbit of the spacecraft

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Spacecraft attitude-track integrated backstepping tracking control method
  • Spacecraft attitude-track integrated backstepping tracking control method
  • Spacecraft attitude-track integrated backstepping tracking control method

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0094] Specific embodiment one: a kind of spacecraft attitude-orbit integration back-step tracking control method comprises the following steps:

[0095] Quaternions and Dual Quaternions

[0096] Quaternions were proposed by Hamilton in 1843, and they are the extension of complex numbers in four-dimensional space, also known as hypercomplex numbers. The quaternion can be expressed as q=[η,ξ], where η is a real number, called the scalar part, ξ=ξ x i+ξ y j+ξ z k is the quaternion vector part, i, j, k are unit direction vectors orthogonal to each other, ξ x , ξ y , ξ z is a real number, representing the components of the quaternion vector part in the three directions of i j k. Define the following dual quaternion algorithm:

[0097] q 1 ±q 2 =[η 1 ±η 2 ,ξ 1 ±ξ 2 ] (1)

[0098] λq=[λη,λξ] (2)

[0099]

[0100]

[0101] q -1 =q* / ||q|| (5)

[0102] Among them, q 1 ,q 2 Both are quaternions, λ is a real number, "." is a quaternion multiplication, q * is the...

specific Embodiment approach 2

[0295] Specific embodiment two: the difference between this embodiment and specific embodiment one is: the specific process of establishing the relative kinematics and dynamics model of the spacecraft attitude and orbit integration based on the dual quaternion in the step one is:

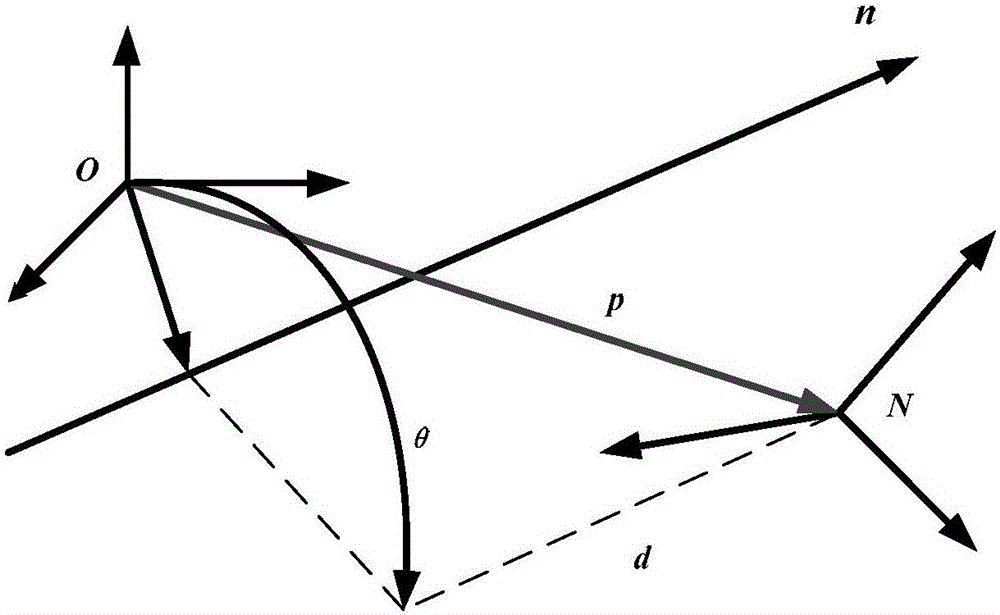
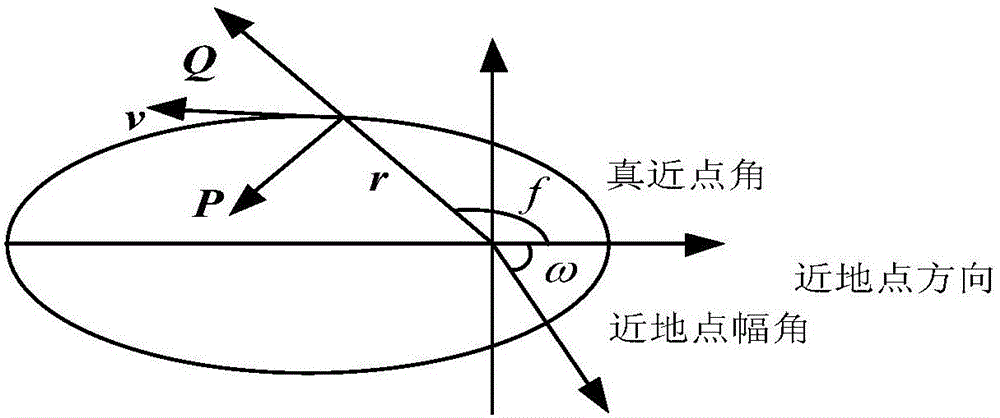
[0296] Define O l -X l Y l Z l is the body coordinate system of the target spacecraft, O f -X f Y f Z f is the body coordinate system of the tracking spacecraft. Use the bias quaternion representation to track the relative motion of the spacecraft:

[0297]

[0298] in is the dual quaternion of the deviation of the spacecraft relative to the target, is the conjugate of the dual quaternion of the target relative to the geocentric inertial coordinate system, is the dual quaternion of the spacecraft relative to the earth-centered inertial coordinate system;

[0299] Deriving formula (81), the relative kinematic equation of the deviation dual quaternion is obtained:

[0300]

[0301...

specific Embodiment approach 3

[0318] Embodiment 3: The difference between this embodiment and Embodiment 1 or 2 is that the specific process of designing the controller based on the backstepping method in the step 2 is:

[0319] The control objective of the present invention is to make the error amount of tracking the state of motion of the spacecraft in consideration of external disturbances as well as which is, in (·) v is the corresponding vector part.

[0320] When there are external disturbances and model uncertainties, (85) can be rewritten as:

[0321]

[0322]

[0323] in for The derivative of the dual part of , for the real part of for The cross product matrix of the dual part, I is the identity matrix, is the nominal part representing the dual inertia matrix, is the controller output, represents the total uncertainty of the model;

[0324] Assuming that the total uncertainty of the system has an upper bound, that is

[0325] definition is the dual part of...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A spacecraft attitude-track integrated backstepping tracking control method is provided, and aims to solve the problems that an existing method respectively uses separate control modes to track the spacecraft track and attitude, so the tracking effect is poor; the method comprises the following steps: 1, building a spacecraft attitude-track integrated relative kinematics and dynamics model according to dual quaternions; 2, designing a controller according to a backstepping method and the spacecraft attitude-track integrated relative kinematics and dynamics model built in step 1; 3, designing an anti-saturation method based input bounded controller according to the controller designed in step 2. The method considers the input bound problems on the backstepping controller base, and designs the anti-saturation node based input bounded backstepping controller; the method can track the spacecraft and realize the 6-degree of freedom attitude-track cooperation tracking of the target spacecraft, is suitable for practical in orbit conditions, and applied to the spaceflight field.

Description

technical field [0001] The invention relates to a space vehicle attitude-orbit integrated back-step tracking control method. Background technique [0002] In 1957, the former Soviet Union launched the first man-made earth satellite, marking a big step forward in human exploration of space. Today, aerospace technology has become one of the most interesting technologies in the world. It promotes the progress of human science and technology, and expands the field of human activities from the atmosphere to the outer space. Among them, various scientific satellites and application satellites serving scientific research, national economy and military have been greatly developed. Satellites have been used in various fields of life, such as reconnaissance and surveillance, navigation and positioning, information transmission, environmental detection, deep space exploration, etc. The field of application has played a vital role and has had an extremely significant impact on human pr...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05D1/08G05D1/10
Inventor 郭延宁刘昱晗吕跃勇王鹏宇马广富
Owner 黑龙江省工研院资产经营管理有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com