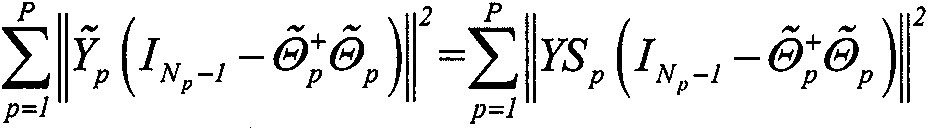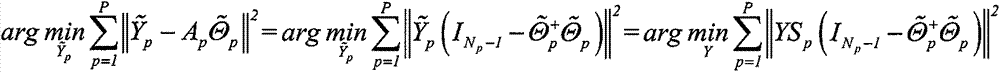Geodesic line preservation-based nonlinear data dimension reduction method
A data dimensionality reduction and geodesic technology, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve problems such as inability to process, and achieve the effect of reducing the number and order of the matrix
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
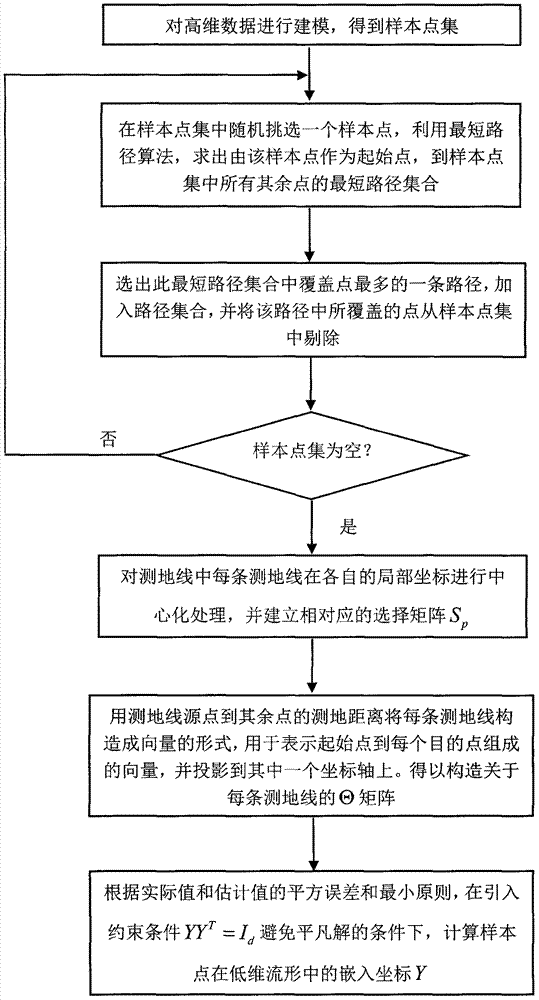
[0016] As shown in the attached figure, the non-linear data dimensionality reduction method based on geodesic preservation includes the following contents:
[0017] 1. Assume that the high-dimensional data sample point set is X=[x 1 … x N ]∈R D×N , the sample point set mapped to the low-dimensional space is Y=[x 1 … x N ]∈R d×N . Among them: D is the dimension of high-dimensional space; d(dD×N The N D-dimensional real column vectors in . Y is the output sample set that maps high-dimensional data to low-dimensional space, and is the low-dimensional space R d×N The N d-dimensional real column vectors in .
[0018] 2. Calculate the Euclidean distance d between adjacent point pairs i and j in the sample point set x (i, j), construct a weighted circulation graph reflecting the neighborhood relationship of the sample point set, and calculate the geodesic distance matrix D corresponding to the sample point set according to the weighted circulation graph.
[0019] 3. Random...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com