Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

SOH (State of Health) estimation method of power cell system based on fractional order model

A power battery, state of health technology, applied in the direction of measuring electricity, measuring electrical variables, measuring devices, etc.

Active Publication Date: 2017-07-25
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF2 Cites 39 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

By establishing the relationship between the peak value of the IC curve and the remaining capacity of the battery, the OCV-SOC curve obtained online can be used to estimate the remaining battery capacity, identify the battery life decline behavior, and overcome the difficulty of estimating the battery capacity online with the existing power battery life evaluation methods defect

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • SOH (State of Health) estimation method of power cell system based on fractional order model
  • SOH (State of Health) estimation method of power cell system based on fractional order model
  • SOH (State of Health) estimation method of power cell system based on fractional order model

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0053] The above is only an overview of the technical solution of the present invention. In order to better understand the technical means of the present invention, the present invention will be further described in detail below in conjunction with the accompanying drawings and specific embodiments.

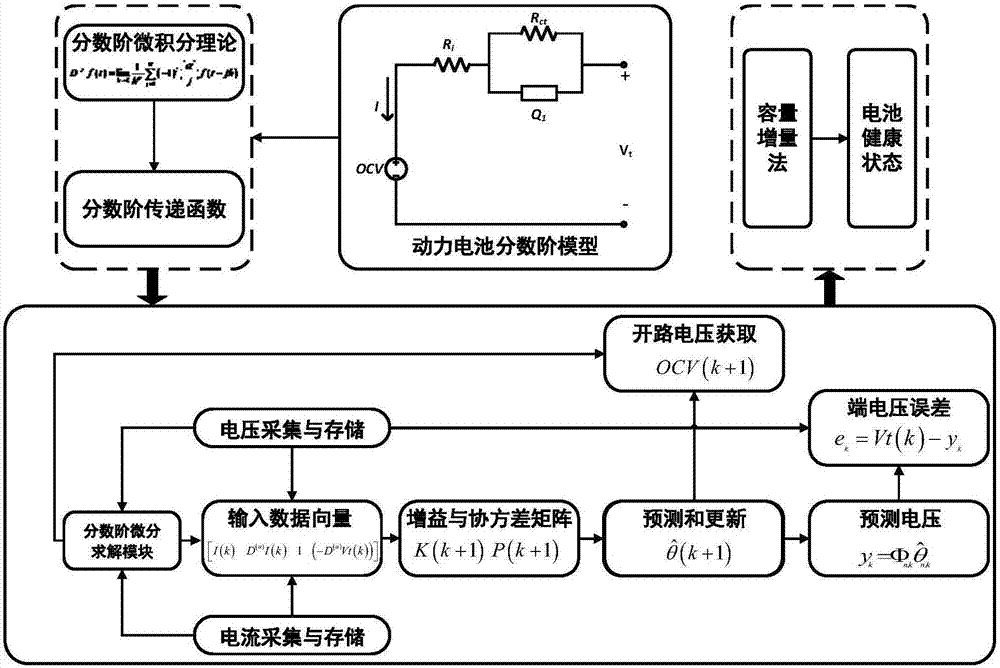
[0054] The method for estimating the state of health of the power battery system provided by the present invention is as follows: figure 1 As shown, it specifically includes the following steps:

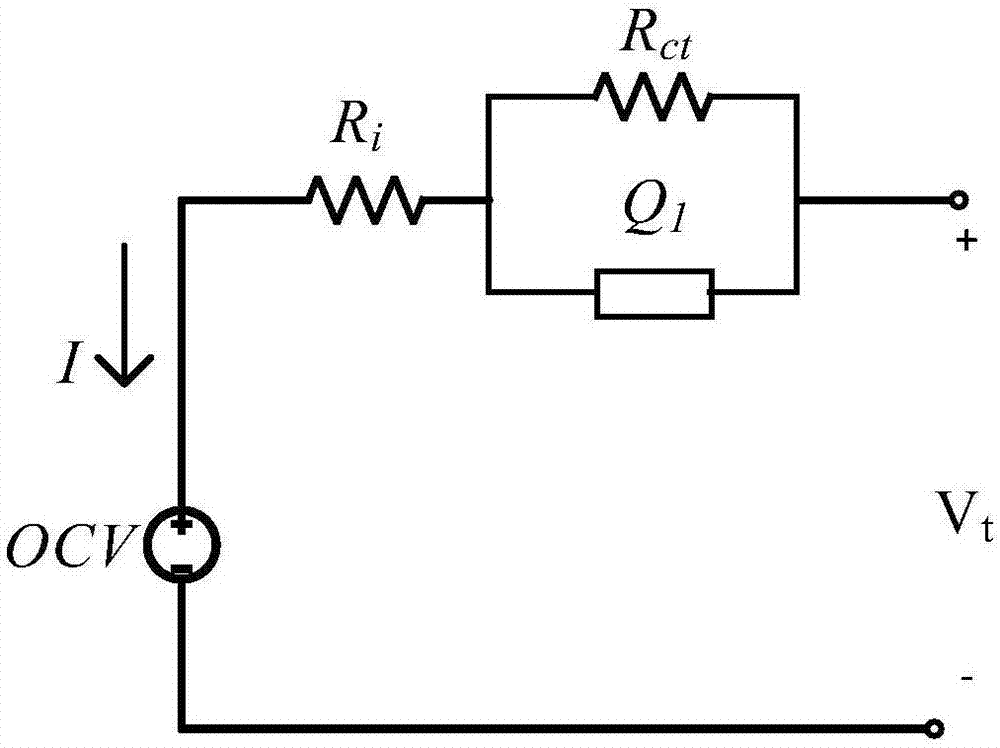
[0055] 1). Establishing a fractional order model of the power battery system, and discretizing the model;

[0056] 2). Carry out real vehicle data collection, and use the least squares method based on the forgetting factor to carry out online identification of the parameter matrix;

[0057] 3). Extracting the open circuit voltage and other impedance parameters in real time from the parameter matrix obtained from the identification.

[0058] 4). Estimate the state of health (SOH) of the ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an SOH estimation method of a power cell system based on a fractional order model. A cell open-circuit voltage is obtained on the basis of the fractional order model, and a capacity incremental method is further combined to estimate the SOH online; the problem that the cell capacity is hard to estimate online via a present power cell life estimation method is solved, the cell open-circuit voltage can be obtained needless of charging / discharging a cell in weak current or keeping the cell standby for a long time, online estimation of the SOH is realized by further combining the capacity incremental method, and the obtained open-circuit voltage can be used for SOC calibration.

Description

technical field [0001] The invention relates to the field of vehicle-mounted power battery systems, in particular to modeling and health state estimation techniques for vehicle-mounted power battery systems. Background technique [0002] The existing battery open circuit voltage is usually obtained in the following two ways: 1. Approximately consider the battery terminal voltage when charging and discharging with a small current is the open circuit voltage; 2. Use the method of standing still for a long time after charging and discharging to obtain the open circuit voltage value of different SOC points . However, the above two methods have relatively strict requirements on the battery charging and discharging current and the resting time, and the long time consumption makes it difficult to apply in real vehicles. [0003] The traditional equivalent circuit model uses ideal circuit components to simulate the characteristics of power batteries, but this model lacks theoretica...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01R31/36
Inventor 熊瑞田金鹏何洪文孙逢春
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com