Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

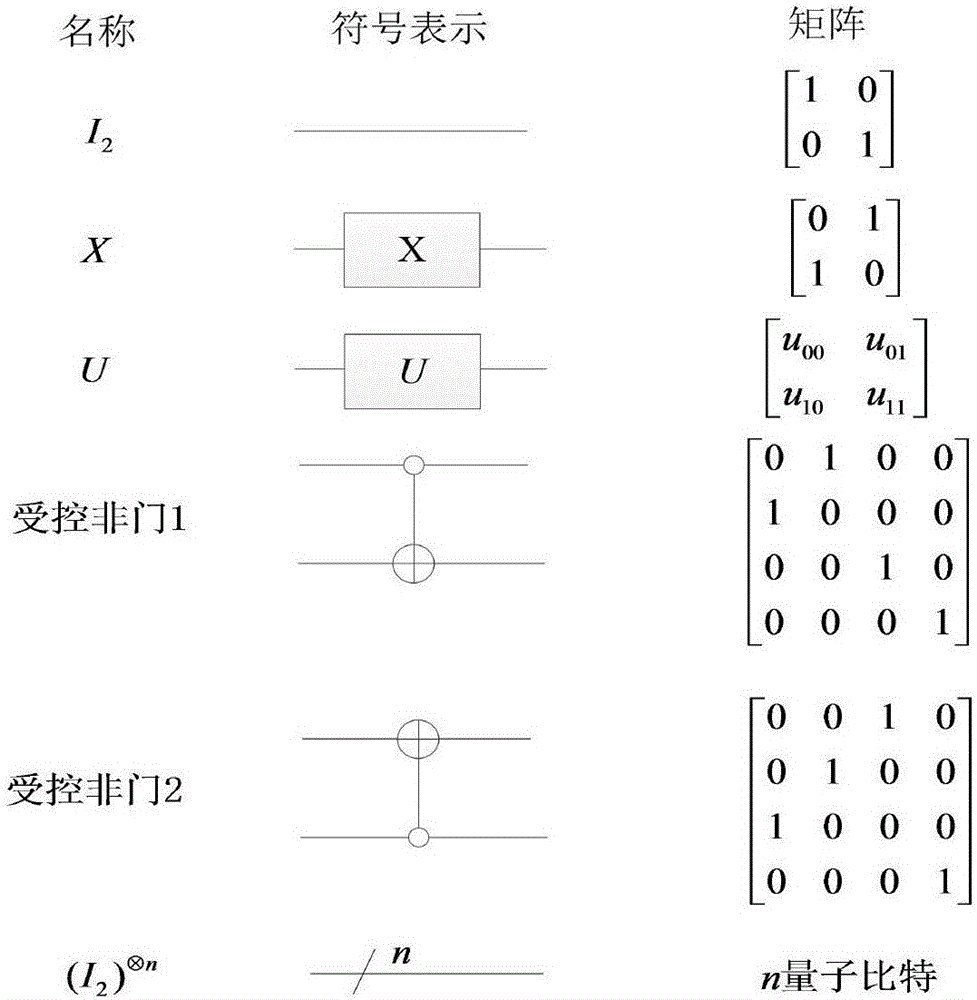
Method for realizing quantum circuit design by quantum D(4) wavelet transform

A technology of wavelet transform and circuit design, applied in computing, special data processing applications, complex mathematical operations, etc., can solve the problems of high complexity in electronic circuit design

Inactive Publication Date: 2017-09-19
GUANGXI NORMAL UNIV
View PDF2 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0017] The invention provides a quantum D (4) Wavelet transform realizes the method of quantum circuit design, solves the existing classical D (4) The high complexity of electronic circuit design realized by wavelet transform

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for realizing quantum circuit design by quantum D(4) wavelet transform
  • Method for realizing quantum circuit design by quantum D(4) wavelet transform
  • Method for realizing quantum circuit design by quantum D(4) wavelet transform

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0071] A quantum D(4) wavelet transform method to realize quantum circuit design, combining quantum computing with classical D (4) Quantum D (4) wavelet transform. Put D (4) Wavelet transform designs a single-layer quantum D based on the extended tensor product operation principle (4) Implementation of wavelet transform line line.

[0072] D. (4) The wavelet kernel matrix is ​​defined as:

[0073]

[0074] in

[0075] can be expressed in tensor product as

[0076]

[0077] in is the tensor product operation symbol, Yes 2 The n times tensor product, And and are two rotation matrices,

[0078] unitary matrix The iterative formula for is as follows:

[0079]

[0080] where X and I 2 yes figure 1 Medium single-qubit gates, is the tensor product operation symbol, Yes 2 Tensor product of n times, the initial value of iteration is Q 2 =X;

[0081] suppose is a 2 n ×2 n The unitary matrix of , compute the tensor product and available ...

Embodiment 2

[0091] A quantum D(4) wavelet transform method to realize quantum circuit design, combining quantum computing with classical D (4) Quantum D (4) wavelet transform. Put D (4) Wavelet transform designs a single-layer quantum D based on the extended tensor product operation principle (4) Realization of wavelet inverse transform line line.

[0092] Taking the inverse of formula (5), we can get D (4) Wavelet Kernel Matrix Inverse Transform Iterative Formula and Unitary Matrix Q 2n Iterative formula:

[0093]

[0094] where the iteration initial value is (Q 2 ) -1 =X;

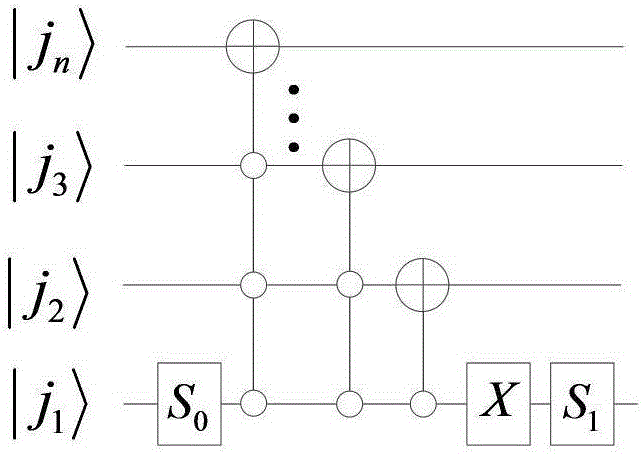
[0095] Combined with formula (6), the single-layer quantum D (4) The quantum implementation circuit of wavelet inverse transform is as follows Figure 5 As shown, its simplified notation is as Figure 6 shown. Depend on Figure 5 Know, single-layer quantum D (4) The complexity of the quantum realization circuit of wavelet inverse transform is Θ(n 2 ).

[0096] The single-layer quantum D designed by...

Embodiment 3

[0100] A quantum D(4) wavelet transform method to realize quantum circuit design, combining quantum computing with classical D (4) Quantum D (4) wavelet transform. Put D (4) Wavelet transform designs K+1 layer quantum D based on the principle of extended tensor product operation (4) Realization circuit of wavelet transform.

[0101] The k+1 layer of quantum D (4) The wavelet transform is defined as Using the extended tensor product, we can get:

[0102]

[0103] where I 2 yes figure 1 Medium single-qubit gates, is the tensor product operation symbol, Yes 2 The n times tensor product, is the k-layer quantum D (4) wavelet transform, is a single-layer quantum D(4) wavelet transform, and the initial value of iteration is 1≤k≤n-2, k and n are both positive integers;

[0104] Combining formulas (5) and (7), in realizing Figure 4 On the basis of the quantum circuit in the k+1 layer quantum D (4) The quantum implementation circuit of wavelet transform is as ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a method for realizing quantum circuit design by quantum D(4) wavelet transform, and belongs to the field of quantum information processing. The method designs single-layer quantum D(4) wavelet transform, uses two rotary matrixes to replace a general unitary matrix and is an innovation for an existing quantum D(4) wavelet transform technology on an aspect of methods. From the complexity analysis of the implementation circuit of the quantum D(4) wavelet transform and quantum D(4) wavelet inverse transform, for a dataset which contains 2n pieces of elements, the complexities of the circuits of the quantum D(4) wavelet transform and the quantum D(4) wavelet inverse transform are both [Theta](n2) which can not be achieved by other classic quick D(4) wavelet transform. The method is suitable for a plurality of practical information processing application fields, for example, algorithms, including image compression, denoising, encryption, decryption and the like, all need efficient D(4) wavelet transform, and the method has an important meaning for the perfection and the application of a quantum computing theory.

Description

technical field [0001] The invention relates to the field of quantum information processing, in particular to a method for realizing quantum circuit design through quantum D(4) wavelet transform. Background technique [0002] Quantum computing is the product of the combination of quantum mechanics and computer science. The parallelism, superposition and measurement uncertainty of quantum computing are fundamental to the superiority of quantum computers over classical computers. In the face of such advantages, the research of quantum information is very necessary. It has become the focus of strategic competition among countries in the world. The national "Thirteenth Five-Year Plan" lists quantum communication and quantum computers as major scientific and technological projects of the national strategic intention (Science and Technology Innovation 2030 -Major projects), and focus on the development of disruptive technologies such as quantum information that lead industrial tra...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/14
CPCG06F17/148
Inventor 黎海生夏海英宋树祥范萍李春雨
Owner GUANGXI NORMAL UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com