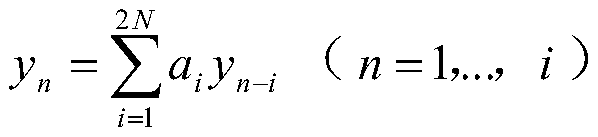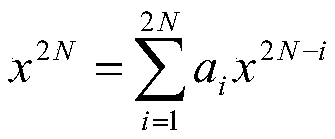A Fast Detection Method of Power System Harmonics Based on Differential Equations
A differential equation and detection method technology, applied in the field of rapid detection of power system harmonics, can solve the problems of FFT algorithm energy leakage, large difference, and complex calculation process of FFT algorithm, etc., and achieve simple calculation method and small data demand Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0033] The preferred embodiments of the present invention will be described in detail below in conjunction with the accompanying drawings, so that the advantages and features of the present invention can be more easily understood by those skilled in the art, so as to define the protection scope of the present invention more clearly.
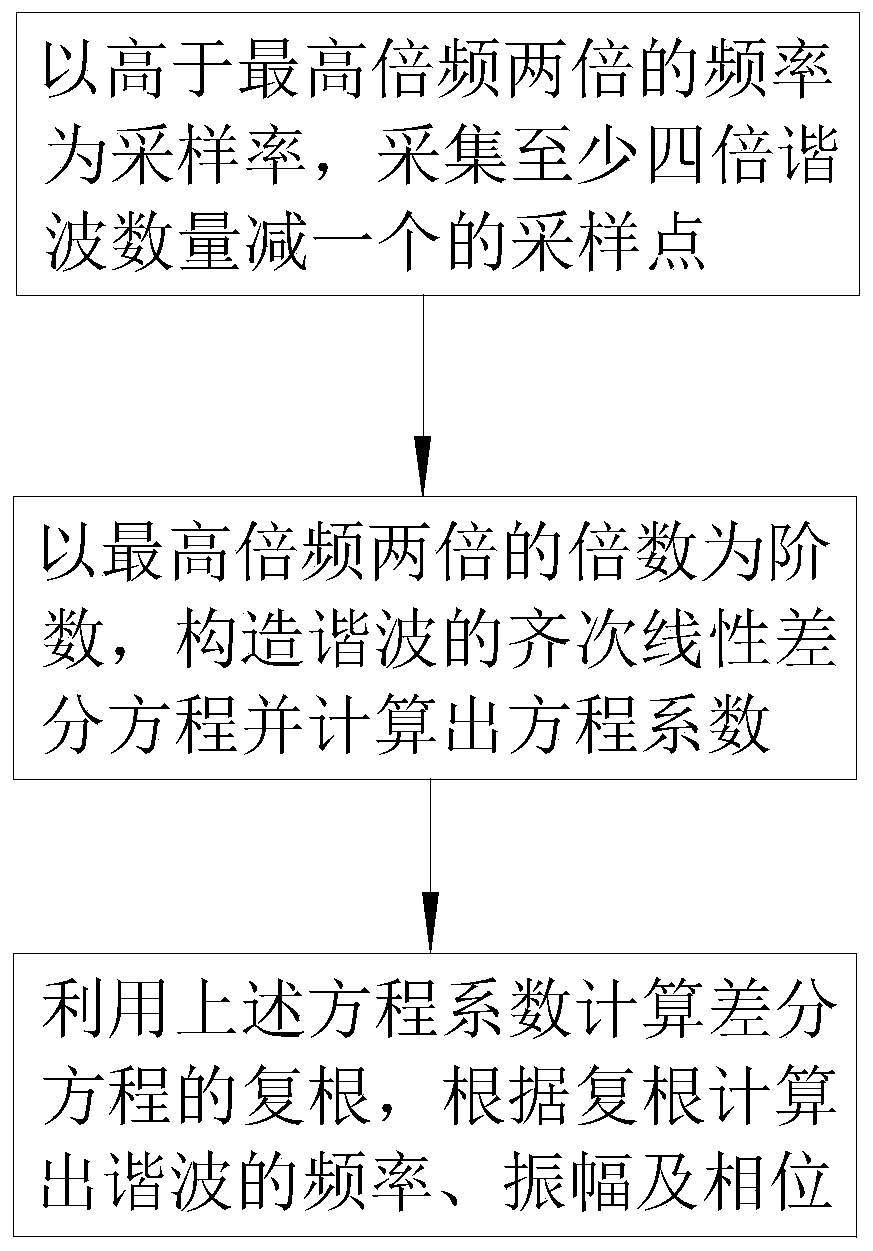
[0034] see figure 1 , the embodiment of the present invention includes:
[0035] A fast detection method of power system harmonics based on differential equations, comprising the following steps:
[0036] 1) Take the frequency higher than twice the highest multiplier as the sampling rate, collect at least four times the number of harmonics minus one sampling point, if the signal noise strength is 1% of the original signal strength, collect the fundamental frequency signal for half a cycle time length If the signal noise intensity is higher than 1%, you can collect signal data longer than half a cycle time length to increase the stability of the ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com