Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Three-dimensional Fourier transformation calculation method and device

A technology of Fourier transform and calculation method, which is applied in the field of three-dimensional Fourier transform calculation method and device, and can solve problems such as large memory consumption and complicated calculation process of three-dimensional Fourier transform

Inactive Publication Date: 2018-01-05
CHINA PETROLEUM & CHEM CORP +1
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The present invention provides a three-dimensional Fourier transform calculation method and device, which are used to solve the technical problems of complex three-dimensional Fourier transform calculation process and large memory consumption in the prior art

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Three-dimensional Fourier transformation calculation method and device
  • Three-dimensional Fourier transformation calculation method and device
  • Three-dimensional Fourier transformation calculation method and device

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

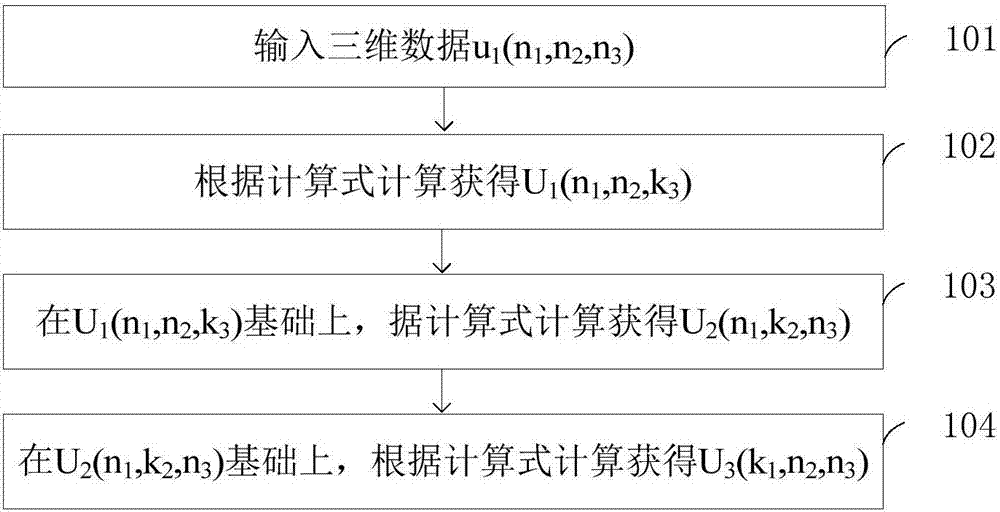
[0060] figure 1 A schematic flow chart of the three-dimensional Fourier transform calculation method provided in Embodiment 1 of the present invention; figure 1 As shown, this embodiment provides a three-dimensional Fourier transform calculation method, including:

[0061] Step 101, input three-dimensional data u(n 1 ,n 2 ,n 3 ), where n i =0~N i -1,i=1,2,3,N i is an integer power of 2.

[0062] For ease of understanding, the three-dimensional signal u(n 1 ,n 2 ,n 3 Each data element in ) is regarded as a point in three-dimensional space, u(n 1 ,n 2 ,n 3 ) represents the spatial coordinates of the point. In this way, the entire 3D signal constitutes a 3D mesh with signal data as nodes. On this 3D mesh body, the 3D DFT calculation process can be understood as the FFT process of performing 1D DFT along the three coordinate axes. The superposition of FFT in these three different directions is the final result of three-dimensional DFT.

[0063] Step 102, according ...

Embodiment 2

[0074]This embodiment is a supplementary description based on the above embodiments.

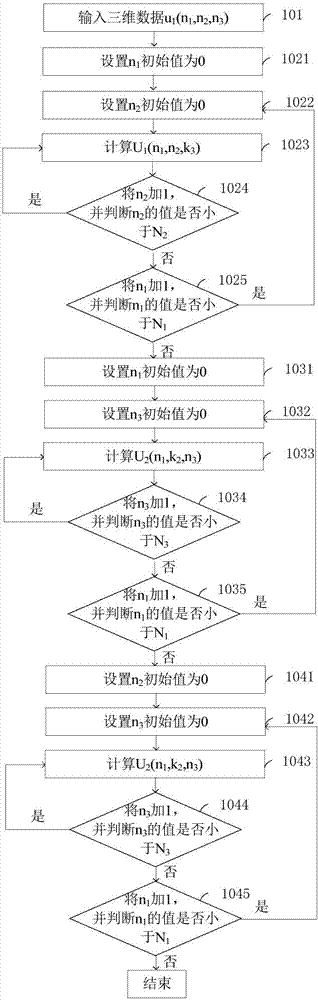
[0075] figure 2 A schematic flow chart of the three-dimensional Fourier transform calculation method provided in Embodiment 2 of the present invention; as figure 2 As shown, this embodiment provides a three-dimensional Fourier transform calculation method, including:

[0076] Step 101, input three-dimensional data u(n 1 ,n 2 ,n 3 ), where n i =0~N i -1,i=1,2,3,N i is an integer power of 2.

[0077] Step 1021, set n 1 The initial value is 0;

[0078] Step 1022, set n 2 The initial value is 0;

[0079] Step 1023, according to the calculation formula Calculate, where, k 3 =0,1,...N 3 -1;

[0080] Step 1024, set n 2 Add 1 and judge n 2 Is the value less than N 2 , if less than, go to step 1023; if not, go to step 1025;

[0081] Step 1025, set n 1 Add 1 and judge n 1 Is the value less than N 1 , if less, go to step 1022; if not, go to step 1031.

[0082] Steps 1021 to 10...

Embodiment 3

[0097] This embodiment is an embodiment of a device, which is used to execute the method in the first embodiment above.

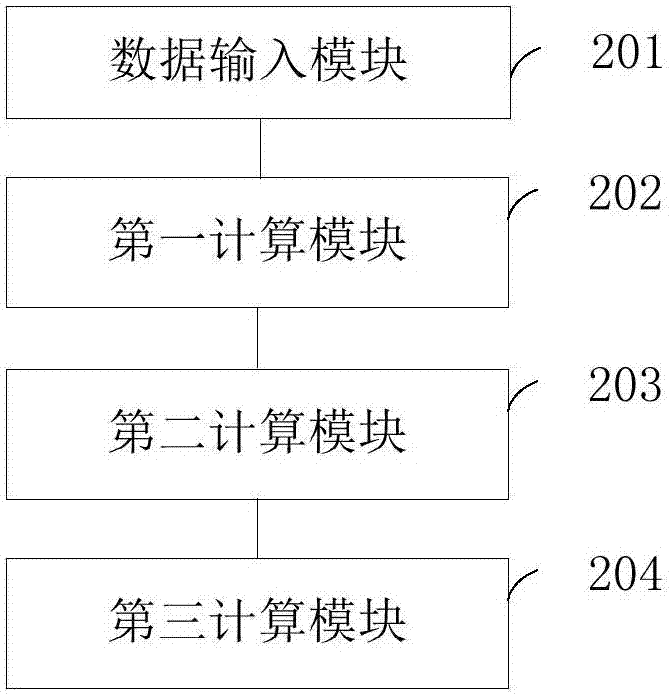
[0098] image 3 A schematic structural diagram of a three-dimensional Fourier transform computing device provided in Embodiment 3 of the present invention; as image 3 As shown, this embodiment provides a three-dimensional Fourier transform computing device, including a data input module 201 , a first computing module 202 , a second computing module 203 and a third computing module 204 .

[0099] Among them, the data input module 201 is used to input three-dimensional data u(n 1 ,n 2 ,n 3 ), where n i =0~N i -1,i=1,2,3,N i is an integer power of 2;

[0100] The first calculation module 202 is used to calculate according to the formula Calculate and obtain the one-dimensional fast Fourier transform, where, k 3 =0,1,...N 3 -1,n 1 =0,1,...,N 1 -1,n 2 =0,1,...,N 2 -1;

[0101] The second calculation module 203 is used to calculate according to...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention provides a three-dimensional Fourier transform calculation method and device, wherein the method includes: input three-dimensional data u(n1, n2, n3), calculate according to the calculation formula; calculate according to the calculation formula; calculate according to the calculation formula to obtain the final transform the result. The calculation result of each step is used as the processing object of the next calculation step, which avoids a lot of extra memory overhead and greatly improves the performance of the program. This performance improvement is especially noticeable when the amount of data is large. While using the above method to increase the memory overhead, the amount of calculation does not increase significantly, and an optimal balance is achieved between the calculation speed and memory consumption.

Description

technical field [0001] The invention relates to the field of numerical calculations, in particular to a three-dimensional Fourier transform calculation method and device. Background technique [0002] As a digital signal analysis and processing method, Fourier transform analysis has been widely used in signal analysis, image processing, pattern recognition and other fields. The numerical calculation of Fourier transform is an important content of Fourier analysis, and it is a bridge from theory to technology of Fourier transform. Discrete Fourier Transform (DFT for short) is the most commonly used and most effective transformation tool, but its direct implementation requires a large amount of calculation. Fast Fourier Transform (Fast fourierTransform, referred to as FFT) is a special fast calculation method for discrete Fourier transform, which can quickly complete the calculation of all points while greatly reducing the amount of calculation. For the FFT of 3D DFT, domest...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/14
Inventor 鄢琦叶欣
Owner CHINA PETROLEUM & CHEM CORP
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com