Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

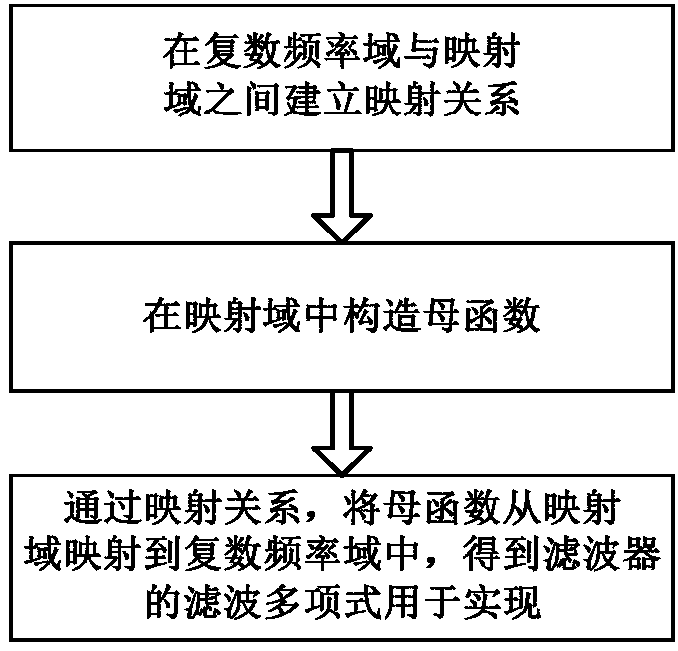
Generalized filter comprehensive method

A synthesis method and filter technology, applied in the generalized synthesis field, can solve problems such as inability to realize asymmetrical frequency response, inability to arbitrarily place transmission zeros, etc.

Inactive Publication Date: 2018-01-09
UNIV OF ELECTRONICS SCI & TECH OF CHINA
View PDF4 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This technical approach has limitations, such as the inability to place transmission zeros arbitrarily; the inability to achieve an asymmetrical frequency response with respect to the center frequency of the passband; etc.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Generalized filter comprehensive method
  • Generalized filter comprehensive method
  • Generalized filter comprehensive method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 2

[0080] Embodiment 2 is also a third-order real coefficient bandpass filter, without loss of generality, the technical index is set as follows: the passband is located at [18, 22]MHz, and the return loss in the passband is greater than 20dB. In order to reflect the flexibility of the design method of the present invention, the two transmission zeros in Embodiment 2 are placed at zero frequency, and the other transmission zero is located at infinite frequency. According to the technical indicators, the filtering polynomial derived from formulas (13a) and (13b) is:

[0081]

[0082]

[0083]

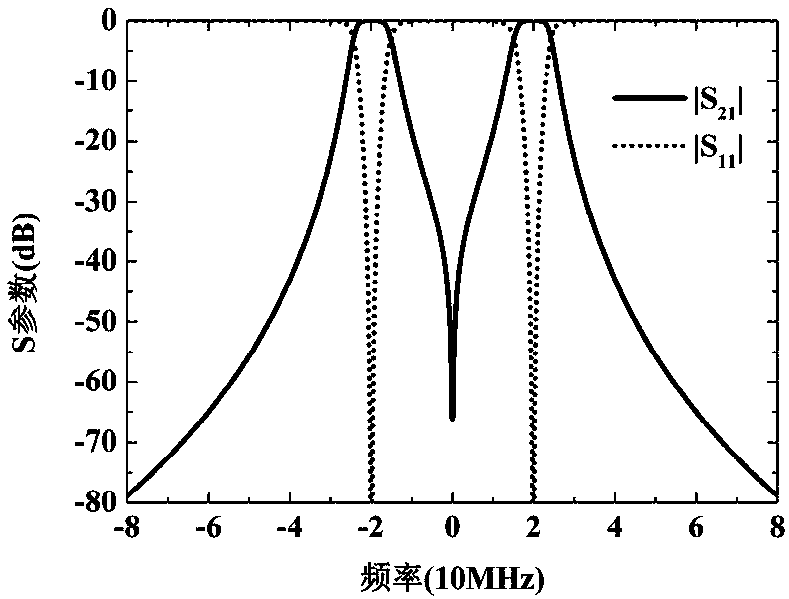
[0084] The frequency response corresponding to the filter polynomial is as follows Figure 4 As shown, it can be seen that the frequency response of the real coefficient bandpass filter is symmetrical about the zero frequency. Since the polarity of the transmission polynomial P is an even function, and the polarity of the reflection polynomial F is also an even function, Embodiment ...

Embodiment 3

[0085] The third embodiment is also a third-order real coefficient bandpass filter, without loss of generality, the technical index is set as follows: the passband is located at [18, 22]MHz, and the return loss in the passband is greater than 20dB. In order to reflect the flexibility of the design method of the present invention, the three transmission zero points in Embodiment 3 are all placed at zero frequency. According to the technical indicators, the filtering polynomial derived from formulas (13a) and (13b) is:

[0086]

[0087]

[0088]

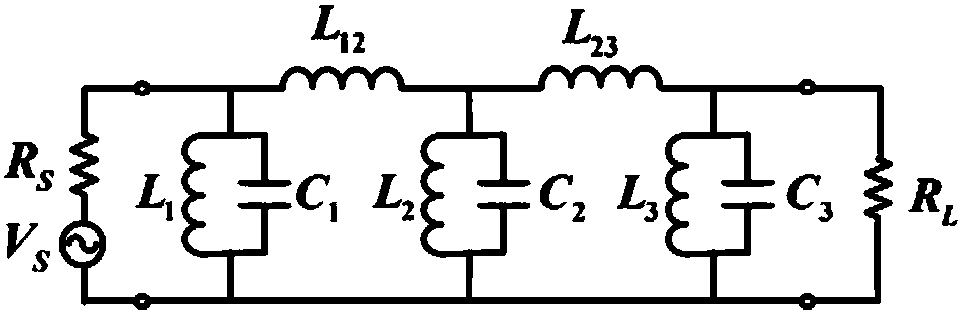
[0089] The frequency response corresponding to the filter polynomial is as follows Figure 6 As shown, it can be seen that the frequency response of the real number bandpass filter is symmetrical about the zero frequency. Using these filtering polynomials, a lumped parameter LC circuit can be used to realize, as Figure 7 shown. Figure 7 The value of the component in: R S =R L =50Ω, L 1 =0.1729μH,L 2 =0.2358μH,L 3 =0....

Embodiment 4

[0090] Embodiment 4 is also a third-order real number bandpass filter, without loss of generality, the technical index is set as follows: the passband is located at [18, 22]MHz, and the return loss in the passband is greater than 20dB. In order to reflect the flexibility of the design method of the present invention, one transmission zero point in Embodiment 4 is placed at zero frequency, one transmission zero point is placed at a limited frequency of 30 MHz, and one transmission zero point is placed at an infinite frequency. According to the technical indicators, the filtering polynomial derived from formulas (13a) and (13b) is:

[0091]

[0092]

[0093]

[0094] The frequency response corresponding to the filter polynomial is as follows Figure 8 As shown, it can be seen that the frequency response of the real coefficient bandpass filter is symmetrical about the zero frequency. Using these filtering polynomials, a lumped parameter LC circuit can be used to realize...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a generalized filter comprehensive method. The whole method comprises the following steps: first step, establishing a mapping relationship between a complex frequency domain anda mapping domain; second step, constructing a generating function in the mapping domain; and third step, mapping the generating function from the mapping domain to the complex frequency domain via the mapping relation, and applying a filtering polynomial of the filter to application. By adoption of the generalized filter comprehensive method, more complex frequency response can be achieved, the transmission zeros can be placed flexibly, and the flexibility is high.

Description

technical field [0001] The invention belongs to the technical field of communication, and in particular relates to a generalized synthesis method of a filter. Background technique [0002] The filter is one of the key components in radar, communication and measurement systems. Its function is to allow the signal of a certain frequency to pass smoothly, while allowing the signal of another part of the frequency to be greatly suppressed. Its performance is important to the performance of the entire system. Impact. The technical indicators of the filter include passband bandwidth, insertion loss, passband ripple, return loss, stopband rejection, in-band phase linearity, and group delay. According to the type of frequency response, it can be divided into elliptic filter, Butterworth filter, Gaussian filter, generalized Chebyshev filter and inverse generalized Chebyshev filter, etc. From the realization form, it can be divided into analog filter and digital filter. For analog ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H03H17/02
Inventor 肖飞
Owner UNIV OF ELECTRONICS SCI & TECH OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com