A 3D inisar imaging method for ship targets with sparse aperture
A technology of sparse aperture and imaging method, which can be applied to instruments, measuring devices, and re-radiation, etc., can solve problems such as low accuracy, and achieve the effect of improving the accuracy of coordinate reconstruction.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
specific Embodiment approach 1
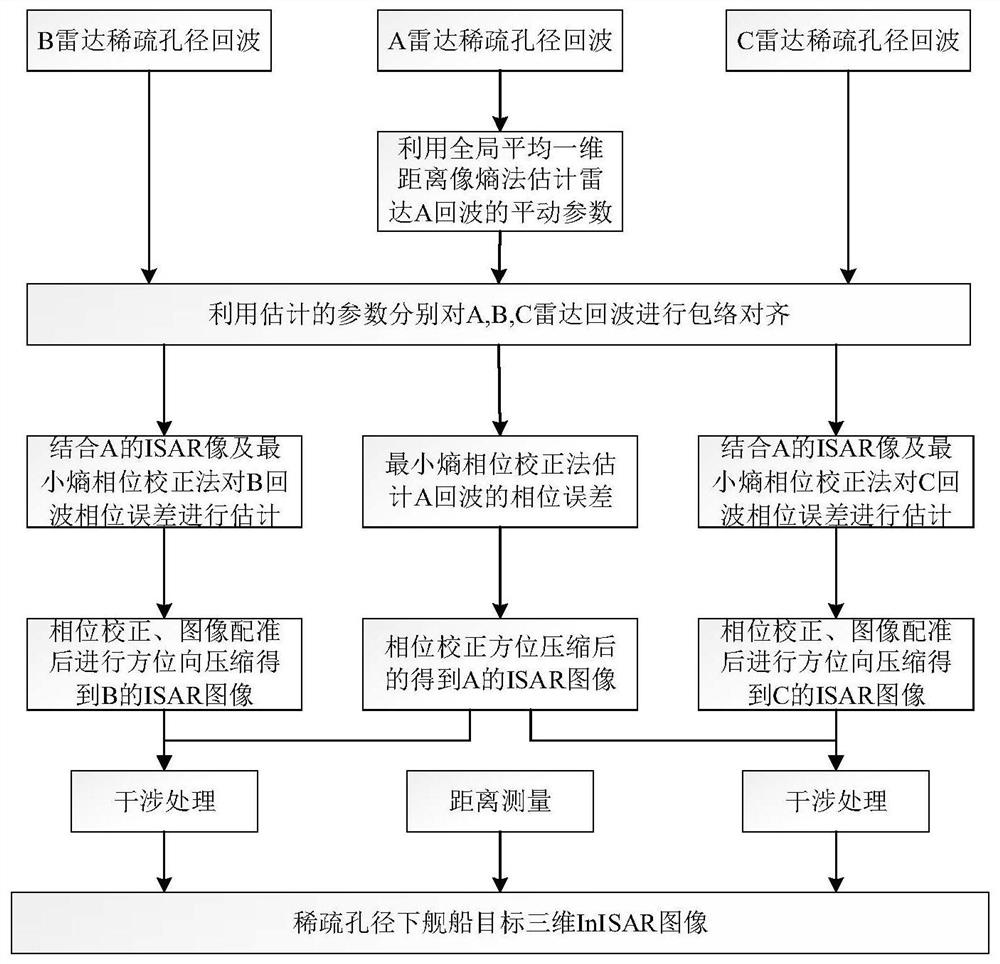
[0014] Specific implementation mode one: combine figure 1 To illustrate this embodiment, the specific process of a three-dimensional InISAR imaging method for a ship target with a sparse aperture in this embodiment is as follows:
[0015] Radars A, B, and C respectively receive sparse aperture echoes. First, the global average one-dimensional range image entropy minimization algorithm is used to estimate the target’s translational parameters for the echoes of radar A, and the optimal estimation of the translational parameters is obtained through step-by-step iterations. value; in order to make each scattering point of the target focus on the same range unit in the three ISAR images obtained by radars A, B, and C, the optimal translation parameters estimated by radar A are compared to radars A, B, and C respectively. The received sparse aperture echoes are compensated to achieve envelope alignment, and the compensated echoes are compressed in the range direction to obtain a on...
specific Embodiment approach 2
[0018] Specific embodiment 2: the difference between this embodiment and specific embodiment 1 is: in said step 2, the method with the smallest global average one-dimensional distance image entropy is adopted for S A The translation component of (m,n) is estimated to obtain the optimal estimate Δr of the translation component; the specific process is:
[0019] Step 21. Given the initial distance vector Δr=0, calculate the global average one-dimensional range image of radar A
[0020] Step 22, calculate the Shannon entropy as
[0021] Step two and three, estimate Δr:
[0022] Δr(m)=max r=1,1,…,N IFFT((FFT(f A (m,r))) * FFT(ln(f Aave (-r))));
[0023] m=1,2,...,M; (·) * To take the conjugate, FFT is Fourier transform, IFFT Fourier inverse transform;
[0024] Step 24: Update the average one-dimensional distance image Calculate the Shannon entropy E again;
[0025] Step 25: Determine whether the entropy E has decreased, and if so, return to Step 2 and 3 to continu...
specific Embodiment approach 3
[0027] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is that the Δr obtained in the step three is used to compensate the echoes of the radars A, B, and C respectively, and the distance of the compensated echoes is calculated. The one-dimensional range image after being compensated for compression; the specific process is:
[0028] In order to ensure accurate interference in 3D imaging, it is necessary to use the translational parameters of radar A to compensate for each radar echo, as follows:
[0029] S A1 (m,n)=S A (m,n)exp(-j2πnΔr(m) / N) (1)
[0030] S B1 (m,n)=S B (m,n)exp(-j2πnΔr(m) / N) (2)
[0031]
[0032] In the formula j is a unit imaginary number; S A1 (m,n) is the echo of radar A after compensation, S B1 (m,n) is the echo of radar B after compensation, S C1 (m,n) is the echo after compensation for radar C; respectively for S A1 (m,n), S B1 (m,n), S C1 (m,n) is compressed in the distance dimension, ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com