Mechanical fault diagnosis method based on parameter adaptive VMD
A technology for mechanical faults and diagnosis methods, applied in the testing of mechanical components, genetic models, genetic laws, etc., can solve problems such as information omission, influence of decomposition results, and difficulty in obtaining satisfactory analysis results, and achieve strong signal detection capabilities and accurate analysis. the effect of the result
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
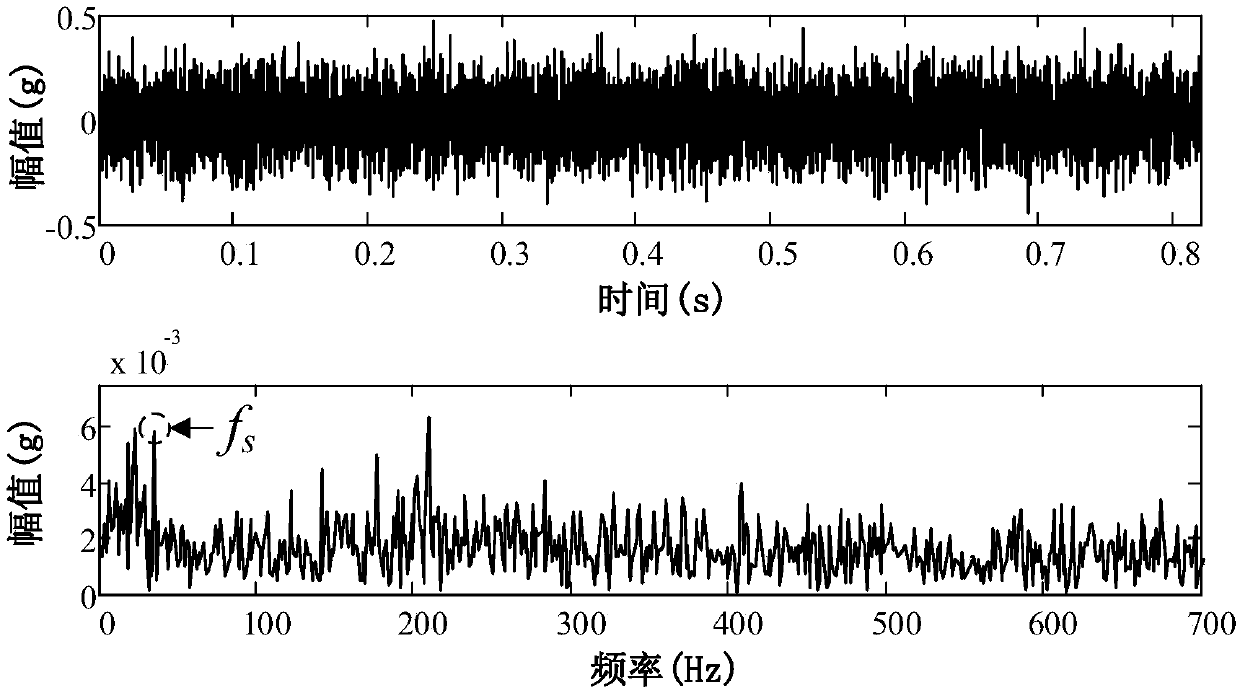
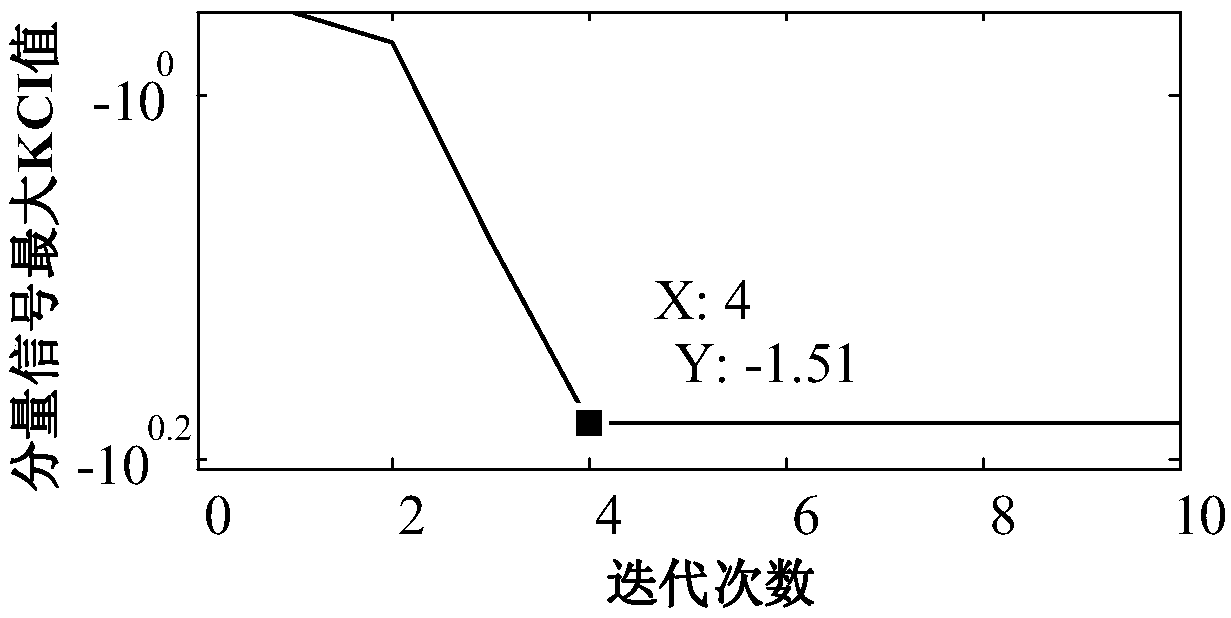
[0052] The present invention uses the weighted kurtosis index (KCI) as the fitness function, through the optimization algorithm to adaptively obtain the VMD decomposition parameters that best match the signal to be analyzed, and uses the best matching VMD decomposition parameters to perform VMD decomposition on the original vibration signal, and then Realize mechanical fault feature extraction and fault diagnosis. Since the weighted kurtosis index comprehensively considers the characteristics of the modal component and the correlation between the modal component and the original signal, using it as the optimization objective function can effectively avoid the problem of information omission, thereby improving the signal detection ability of the VMD method in mechanical fault diagnosis , to achieve accurate diagnosis of mechanical failures.
[0053] The embodiment provides a mechanical fault diagnosis method, the workflow is as follows figure 1 As shown, the specific steps are...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com