Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Instantaneous frequency analysis and diagnosis method aiming at bearing vibration signal

A technology of instantaneous frequency and diagnosis method, which is applied in measuring devices, instruments, and ultrasonic/sonic/infrasonic waves, etc., can solve the problems of inaccurate estimation of instantaneous frequency, difficult to effectively decompose, blurred spectrum, etc., to improve separation accuracy, The effect of solving spectral blur problem and improving estimation accuracy

Inactive Publication Date: 2018-11-30
SHENYANG UNIV
View PDF0 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Under the condition of variable speed, the vibration signal of the bearing has the characteristics of nonlinearity, time-varying, modulation and multi-component characteristics, and the harmonic components are very similar or even overlapped. The frequency analysis method is difficult to effectively decompose it, resulting in blurred spectrum and inaccurate instantaneous frequency estimation, etc. These problems need to be further solved

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Instantaneous frequency analysis and diagnosis method aiming at bearing vibration signal
  • Instantaneous frequency analysis and diagnosis method aiming at bearing vibration signal
  • Instantaneous frequency analysis and diagnosis method aiming at bearing vibration signal

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0032] Step 1: Bearing vibration signal under variable speed conditions ,Described as follows:

[0033]

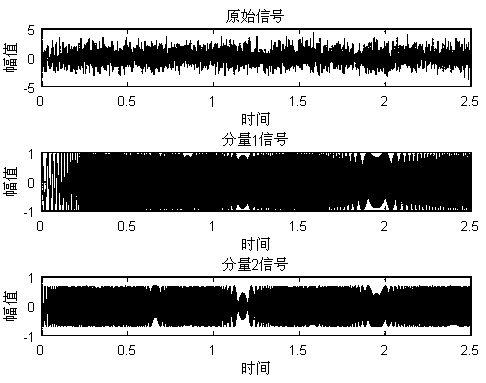
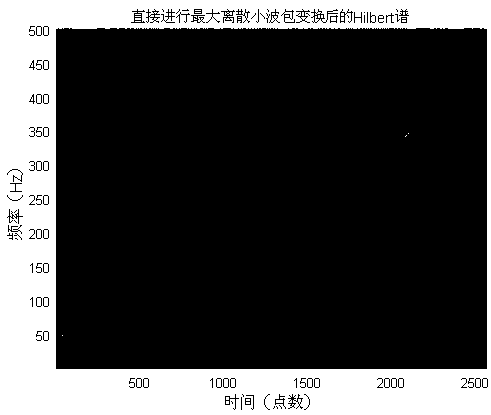
[0034] in, It is Gaussian white noise, the signal-to-noise ratio is 3dB, the sampling frequency is 1024Hz, and the sampling time is 2.5s. The time domain waveform of figure 2 shown. right Carry out the maximum discrete wavelet packet transform, when the frequency spectrum is as image 3 Shown; use the maximum energy method to separate out the harmonic components with the most significant energy in the spectrogram , for the next analysis.

[0035] Step 2: Use the least squares method to fit the harmonic components obtained in step 1 , and then get its phase function

[0036] .

[0037] Step 3: To vibration signal Carry out Hilbert transform to get the analytical signal ,in yes The Hilbert transform.

[0038] Step 4: According to the phase function obtained in step 2 ,right Perform generalized demodulation to get the signal .

[0039] Ste...

Embodiment 2

[0045] Step 1: Bearing vibration signal under variable speed conditions ,Described as follows:

[0046] in , the sampling frequency of the signal is 1024Hz, the sampling time is 1s, the signal The time domain waveform of Image 6 shown. right Carry out the maximum discrete wavelet packet transform, when the frequency spectrum is as Figure 7 Shown; use the maximum energy method to separate out the harmonic components with the most significant energy in the spectrogram , for the next analysis.

[0047] Step 2: Use the least squares method to fit the harmonic components obtained in step 1 , to obtain the fundamental frequency component containing the rotational speed information; and use the curve fitting function to obtain the parameters of the phase function, and finally obtain the phase function .

[0048] Step 3: To vibration signal Carry out Hilbert transform to get the analytical signal ,in yes The Hilbert transform.

[0049] Step 4: According to...

Embodiment 3

[0056] Step 1: Bearing vibration signal under variable speed conditions ,Described as follows:

[0057]

[0058] Among them, the sampling frequency of the signal is 1024Hz, the sampling time is 1s, and the signal The time domain waveform of Figure 10 shown. right Carry out the maximum discrete wavelet packet transform, when the frequency spectrum is as Figure 11 Shown; use the maximum energy method to separate out the harmonic components with the most significant energy in the spectrogram , for the next analysis.

[0059] Step 2: Use the least squares method to fit the harmonic components obtained in step 1 , to obtain the fundamental frequency component containing the rotational speed information; and use the curve fitting function to obtain the parameters of the phase function, and finally obtain the phase function .

[0060] Step 3: To vibration signal Carry out Hilbert transform to get the analytical signal ,in yes The Hilbert transform.

[0061...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an instantaneous frequency analysis and diagnosis method aiming at a bearing vibration signal, and relates to an analysis and diagnosis method of a bearing component. The method comprises the steps of performing maximum discrete wavelet transformation on the bearing vibration signal x(t), using a maximum energy method for separating a harmonic component with the most significant energy from a time-frequency spectrum, fitting the harmonic component by using a least square method, and thus acquiring a phase function s(t); then performing generalized demodulation analysison the vibration signal x(t) according to the acquired phase function s(t), and building a bandpass filter for filtering; and at last, performing inverse generalized demodulation on the harmonic component after bandpass filtering, estimating instantaneous frequency of the signal after inverse generalized demodulation, performing curve fitting on the instantaneous frequency, and at last acquiring estimated instantaneous frequency of the vibration signal x(t). The method provided by the invention is applied to estimating the instantaneous frequency of the bearing vibration signal so as to achieve tachometer-free order-ratio tracking and analysis, and fault diagnosis and prediction and health management of the bearing under the variable-speed working condition are achieved.

Description

technical field [0001] The invention relates to a method for analyzing and diagnosing bearing components, in particular to a method for analyzing and diagnosing the instantaneous frequency of bearing vibration signals. Background technique [0002] Bearings are key components in industrial production equipment. Due to long-term continuous work under high load and high speed, the proportion of failures is extremely high. At the same time, all kinds of rotating machinery and equipment continue to develop in the direction of complexity, high speed and high efficiency, and the requirements for speed are increasing day by day. The impact of speed fluctuation on bearing fault diagnosis can no longer be ignored. However, from another point of view, in the process of changing the speed, some originally weak fault information will be strengthened instead, which also brings favorable factors to its diagnosis. [0003] The vibration signal of the variable speed bearing has time-varyin...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01H17/00
CPCG01H17/00
Inventor 齐晓轩原忠虎刘英英杜英魁都丽
Owner SHENYANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com