Supercharge Your Innovation With Domain-Expert AI Agents!

A collaborative signature method and system for communication parties based on sm2 algorithm

A technology for communication parties and both parties, applied in the fields of information security and cryptography applications, can solve the problems of low latency, large amount of communication data, and complex computing process, and achieve low latency, small amount of communication data, and low complexity. Effect

Active Publication Date: 2021-03-02
ZHENGZHOU XINDA JIEAN INFORMATION TECH
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Based on this scheme, some algorithms have been proposed, but most of these algorithms have complex calculation processes, more interactive content, and a large amount of communication data. They cannot meet the application requirements of low latency and less interaction in cloud computing, Internet of Things and other environments.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A collaborative signature method and system for communication parties based on sm2 algorithm
  • A collaborative signature method and system for communication parties based on sm2 algorithm
  • A collaborative signature method and system for communication parties based on sm2 algorithm

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

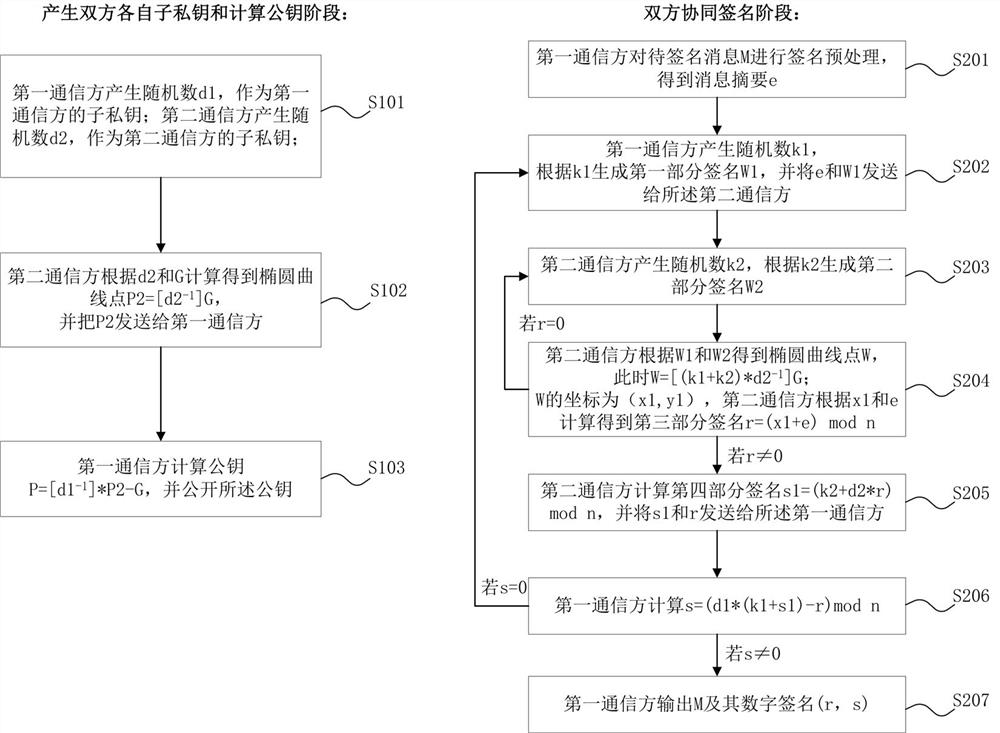
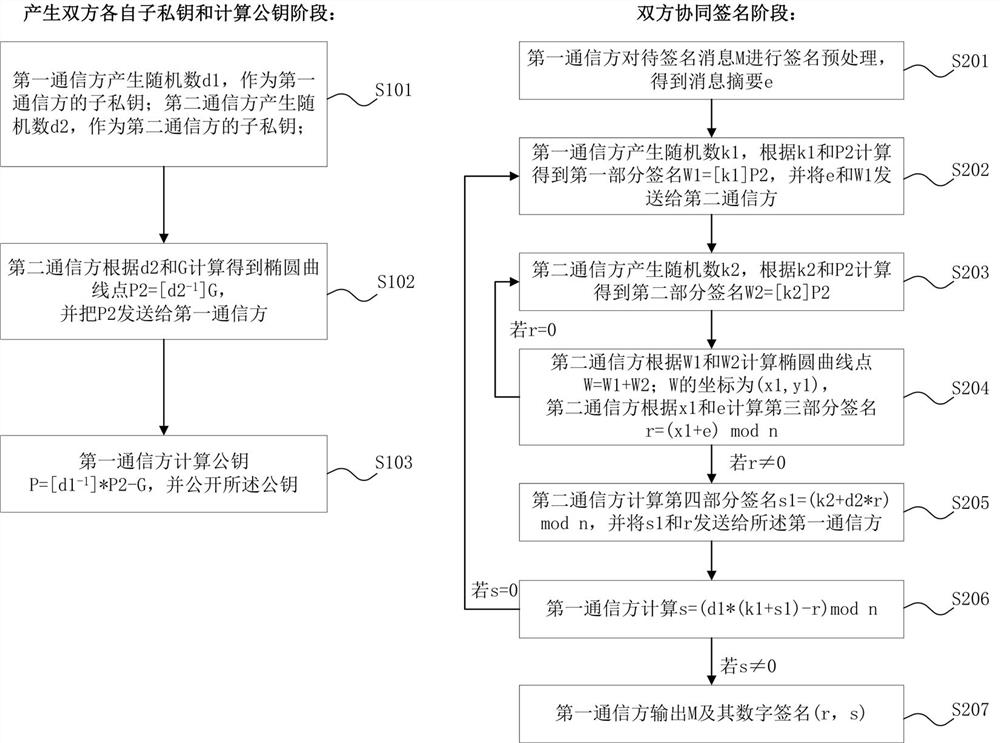
[0058] Such as figure 1 As shown, a cooperative signature method of both communication parties based on the SM2 algorithm, the method involves the first communication party and the second communication party, and the first communication party and the second communication party share the SM2 algorithm elliptic curve E and E The base point G whose upper order is n; the method comprises the following steps:

[0059] 1. The stage of generating the respective sub-private keys of both parties and calculating the public key

[0060] S101. The first communication party generates a random number d1∈[1,n-1] as the sub-private key of the first communication party; the second communication party generates a random number d2∈[1,n-1] ], as the sub-private key of the second communicating party;

[0061] S102. The second communication party calculates and obtains the elliptic curve point P2=[d2 according to d2 and G -1 ]G, and send P2 to the first communication party, where d2 -1 Represen...

Embodiment 2

[0085] Based on the same inventive concept as the above-mentioned method, as figure 2As shown, this embodiment is a preferred specific implementation of the collaborative signature method, and the difference from Embodiment 1 is that steps S202, S203, and S204 are respectively:

[0086] S202. The first communication party generates a random number k1∈[1,n-1], calculates the first part signature W1=[k1]P2 according to k1 and P2, and signs the message digest e and the first part W1 is sent to the second communication party;

[0087] S203. The second communication party generates a random number k2∈[1,n-1], and calculates the second part signature W2=[k2]P2 according to k2 and P2;

[0088] S204. The second communication party calculates the elliptic curve point W=W1+W2 according to the first partial signature W1 and the second partial signature W2, and the coordinates of W are (x1, y1); then according to x1 and the The message digest e is calculated to obtain the third part of...

Embodiment 3

[0099] Based on the same inventive concept as the above-mentioned method, as image 3 As shown, this embodiment is another preferred specific implementation of the cooperative signature method, and the difference from Embodiment 1 is that steps S202, S203, and S204 are respectively:

[0100] S202. The first communication party generates a random number k1∈[1,n-1], calculates the first partial signature W1=[k1]G according to k1 and G, and sends e and W1 to the second communication party ;

[0101] S203. The second communication party generates a random number k2∈[1,n-1], and calculates the second part signature W2=[k2]G according to k2 and G;

[0102] S204. The second communication party calculates the elliptic curve point W=[d2 according to the first partial signature W1 and the second partial signature W2 -1 ]W1+[d2 -1 ] W2, the coordinates of W are (x1, y1); then calculate the third part of the signature r=(x1+e)mod n according to x1 and e, if r=0, return to S203.

[010...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a cooperative signature method and a system for both sides of communication based on an SM2 algorithm, which relates to a first communication party and a second communication party. The communication parties independently generate respective sub-private keys, the public keys are generated by the cooperative operation of the two sub-private keys, and the private keys can notbe calculated by the parameters generated and obtained by the both sides. When signing, both parties of the communication produce partial signatures respectively, and then the final signature result is calculated by the two parties according to the message digest and the parameters such as the respective sub-private key, etc. Neither party of the intrusion is unable to obtain the private key to forge the signature. The technical scheme of the invention fully guarantees the security of the private key of the SM2 algorithm, and in the collaborative signature process, the content of the interaction between the two parties is small, the communication data quantity is small, the complexity of the cryptographic operation is low, and the application requirements of low delay and less interactionin the cloud computing and the Internet of Things environment can be well met.

Description

technical field [0001] The invention relates to the technical fields of information security and cryptography application, in particular to a method and system for cooperative signature of communication parties based on SM2 algorithm. Background technique [0002] Cryptography is the core technology of information security. The Elliptic Curve Public Key Cryptography (ECC) algorithm has been greatly developed and widely used in recent years. The State Cryptography Administration released the Elliptic Curve Public Key Cryptography Algorithm SM2 on December 17, 2010. Authentication and other applications have played an important security role. [0003] In the public key cryptosystem, ensuring the security of the private key is a very important issue. The user's private key usually needs to be safely stored and used in specialized cryptographic hardware, and the private key cannot be derived from the cryptographic hardware. However, with the popularization of the application ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/32H04L9/08
CPCH04L9/0825H04L9/0838H04L9/0861H04L9/3247H04L9/3252
Inventor 赵国磊刘熙胖廖正赟彭金辉刘长河
Owner ZHENGZHOU XINDA JIEAN INFORMATION TECH
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com