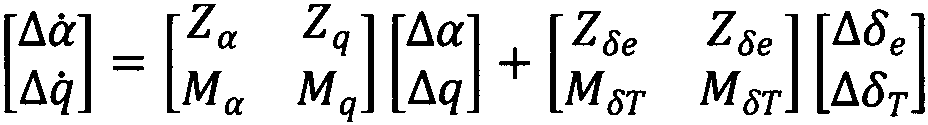Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

A formal verification method of Laplace transform based on Coq

A technology of Laplace transform and formal verification, applied in the field of formal verification, can solve problems such as inability to accurately verify Laplace transform, and achieve the effect of avoiding errors

Inactive Publication Date: 2019-03-29
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF1 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] [Purpose of the invention]: In order to solve the problem that the traditional method cannot accurately verify the Laplace transform, the present invention proposes to formally define the Laplace transform in the theorem prover Coq and verify the basic properties of the Laplace transform , according to the reliability and completeness of the theorem proof, replace the previous method of paper and pen calculation and numerical calculation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A formal verification method of Laplace transform based on Coq
  • A formal verification method of Laplace transform based on Coq
  • A formal verification method of Laplace transform based on Coq

Examples

Experimental program
Comparison scheme
Effect test

Embodiment example

[0066] The invention can be used to verify the derivation process of the short-period motion transfer function model transfer function matrix in the flight control system. The following are the equations of motion for the aircraft:

[0067]

[0068] make

[0069] Among them, A and B are second-order real matrices, and X and U are two-dimensional function vectors. The above equation of motion is equivalently described as:

[0070]

[0071] The key step in deriving the transfer matrix is ​​to perform Laplace transform on both ends of the motion equation under the zero initial condition, apply the properties of Laplace transform, and deduce X(s)=(SI-A)BU(s), as follows In Coq, the above kinematic equation is introduced as a hypothesis, which is the starting point of the proof work.

[0072] Hypothesis e: derive_RV2 X = RF2_plus(RF2_cmul A X)(RF2_cmul B U).

[0073] Transfer matrix inference result: X(s)=(SI-A)BU(s)

[0074] Theorem result: verify_pre X U s ->

[007...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a formal verification method of Laplace transform based on Coq, which formally defines the Laplace transform in the theorem prover Coq and verifies the main properties of the Laplace transform. As that theorem prove Coq is precise and reliable, the method solves the disadvantage that the traditional method cannot accurately verify the Laplace transform. the method mainly includes the following steps: (1) The definition of Laplace transform is formalized by using the theories of differential, integral, limit, complex number and complex variable function in theorem proverCoq; (2) the formalization of the existence theorem of Laplace transform: the formalization of the existence theorem of Laplace transform; (3) The formal proof of the basic properties of Laplace transform: The linear properties, frequency shift properties, differential properties and integral properties of Laplace transform are formally proved in Coq theorem prover.

Description

technical field [0001] The invention discloses a Coq-based Laplace transformation formal verification, which is mainly used for the verification of safety-critical control systems. The invention belongs to the field of formal verification, and is a safety and reliability verification method based on a theorem prover. Background technique [0002] The scale of modern embedded software is getting larger and larger, and traditional software testing techniques are difficult to guarantee the correctness of system functions. On the other hand, the loopholes of the system provide opportunities for hackers to intrude, seriously affecting the security of the system. This situation makes the information industry rethink traditional software development methods, so various formal methods and model-based methods are introduced into the software development process, a typical example is the use of SCADE systems for modeling, development and verification of flight control software. Alt...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/13
CPCG06F17/13
Inventor 陈钢汪一飞
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com