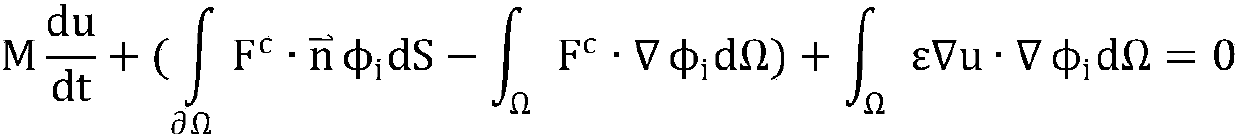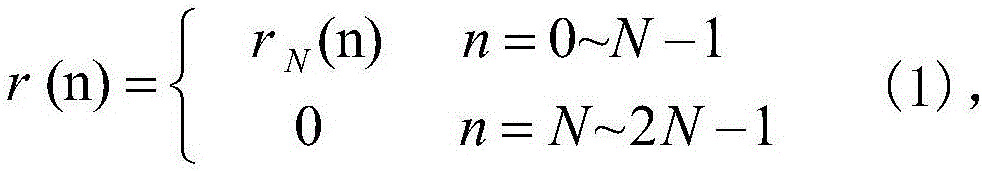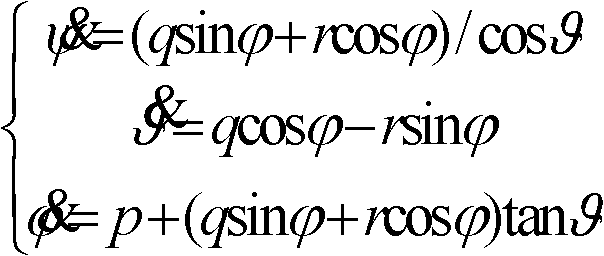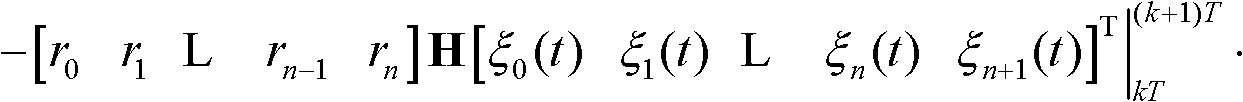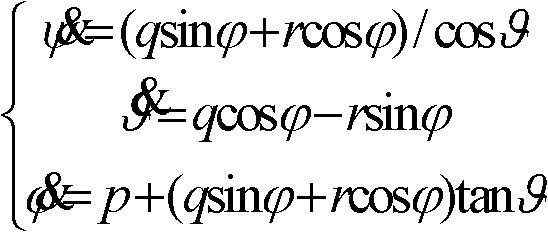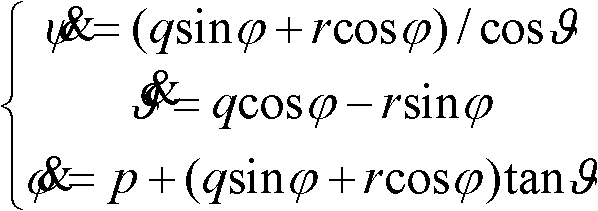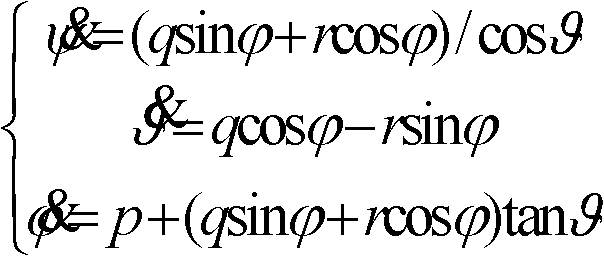Patents
Literature
33 results about "Integral of secant cubed" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
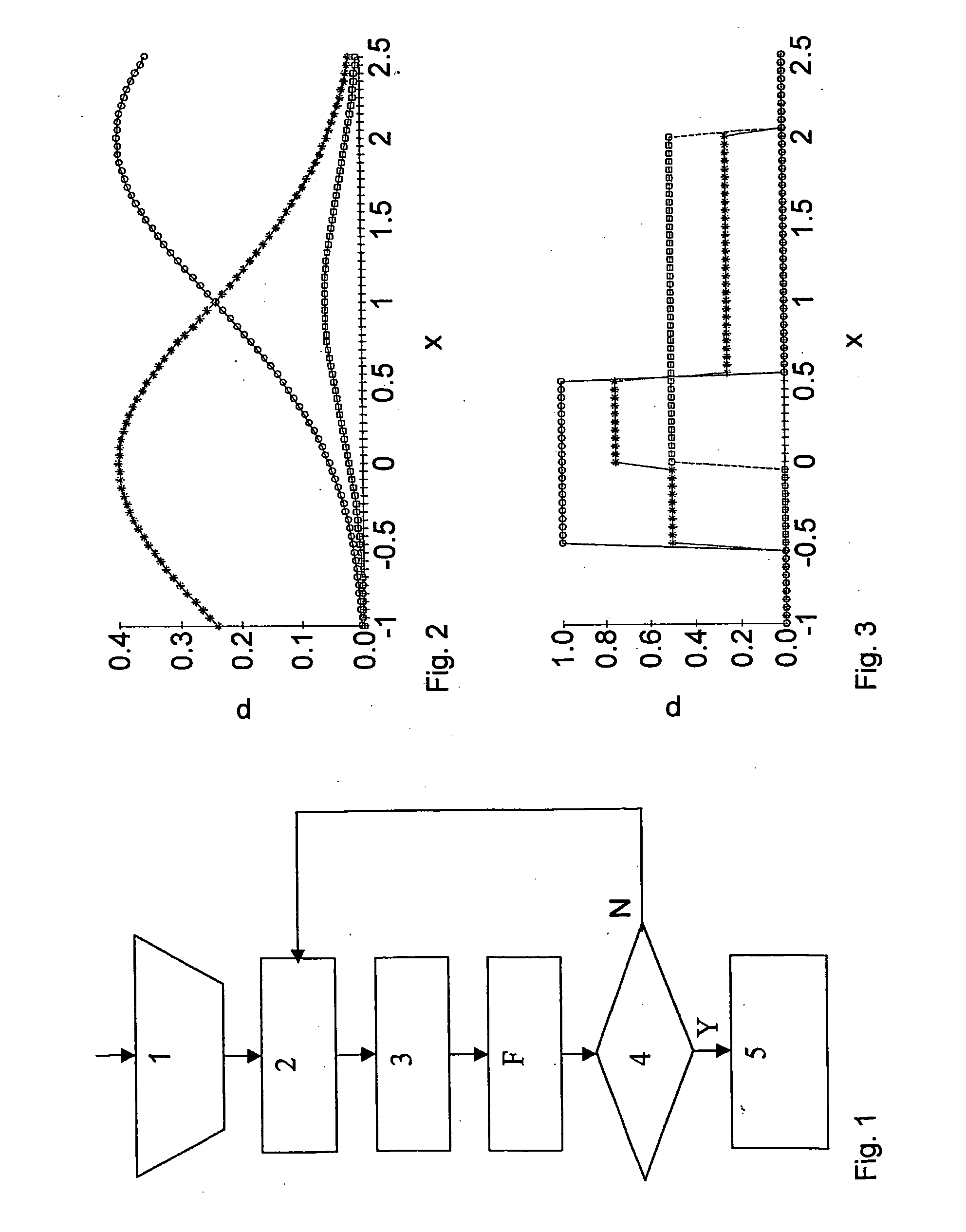
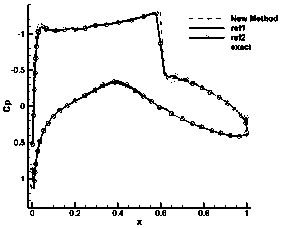
The integral of secant cubed is a frequent and challenging indefinite integral of elementary calculus: ∫sec³x dx=1/2(secxtanx+ln|secx+tanx|)+C. There are a number of reasons why this particular antiderivative is worthy of special attention: The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simplest case. The other cases are done in the same way.
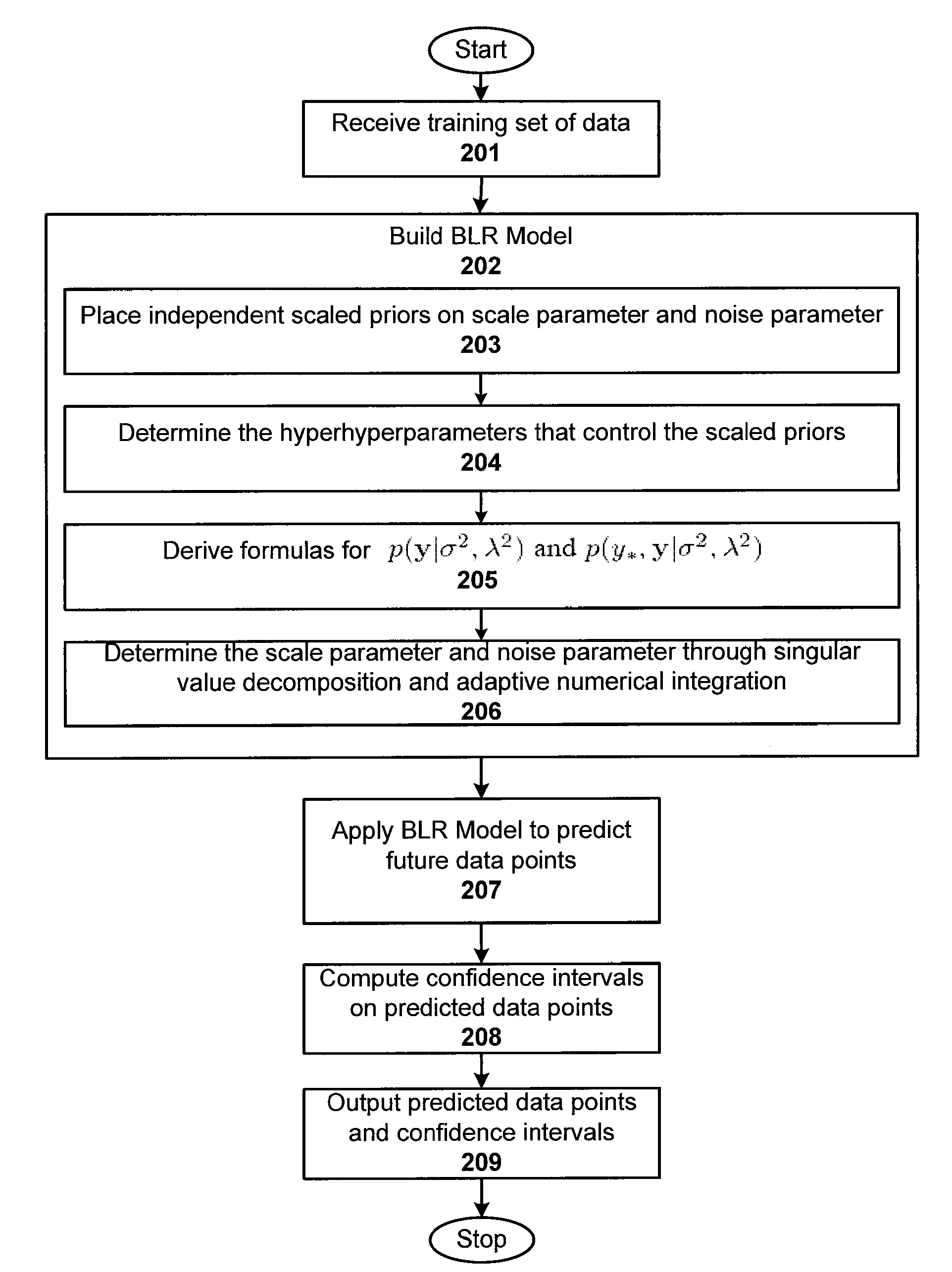
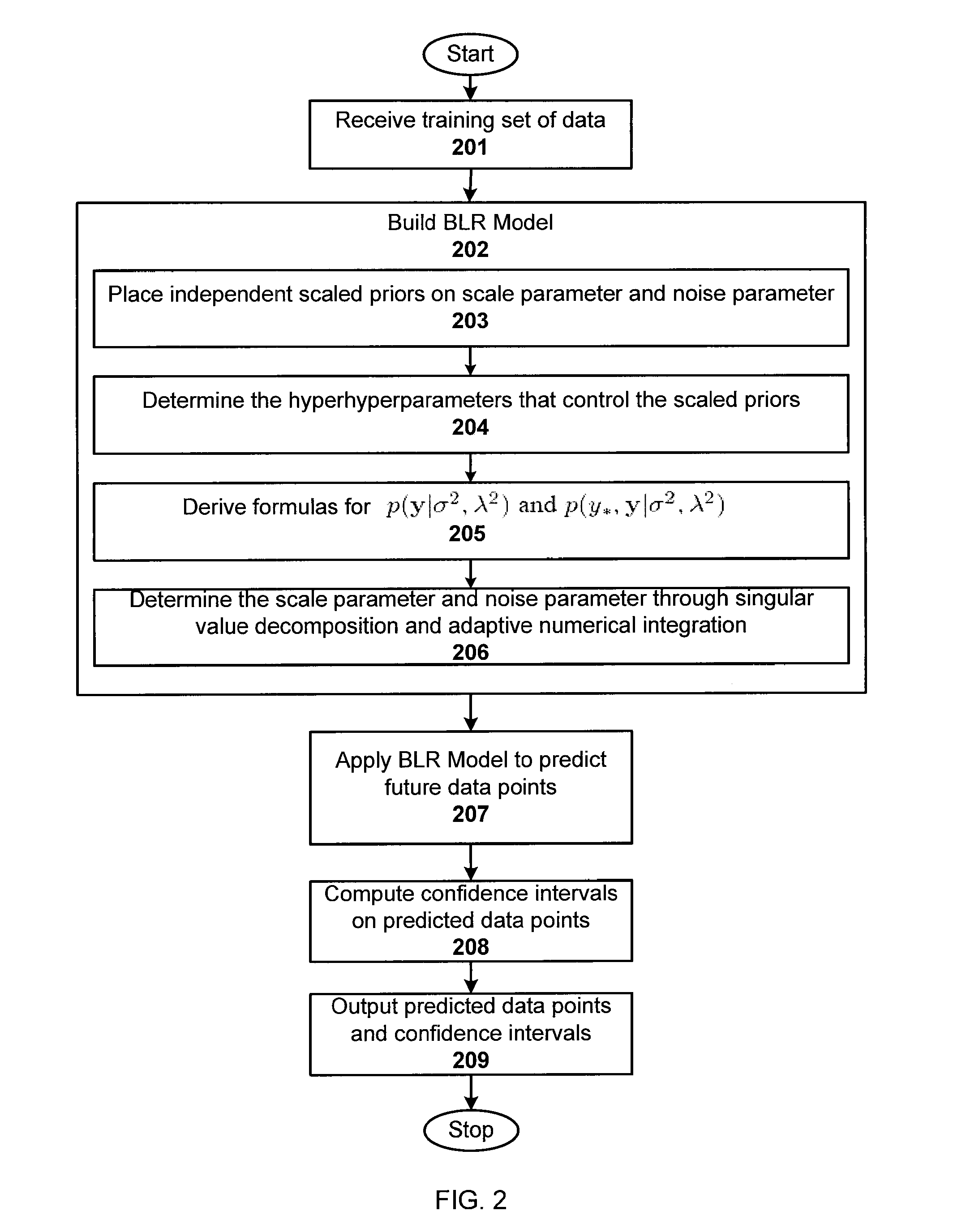
Fully Bayesian Linear Regression
ActiveUS20080162386A1Prevent overfittingDigital computer detailsDigital dataLinear regressionHyperparameter
A simple yet powerful Bayesian model of linear regression is disclosed for methods and systems of machine learning. Unlike previous treatments that have either considered finding hyperparameters through maximum likelihood or have used a simple prior that makes the computation tractable but can lead to overfitting in high dimensions, the disclosed methods use a combination of linear algebra and numerical integration to work a full posterior over hyperparameters in a model with a prior that naturally avoids overfitting. The resulting algorithm is efficient enough to be practically useful. The approach can be viewed as a fully Bayesian version of the discriminative regularized least squares algorithm.
Owner:HONDA MOTOR CO LTD
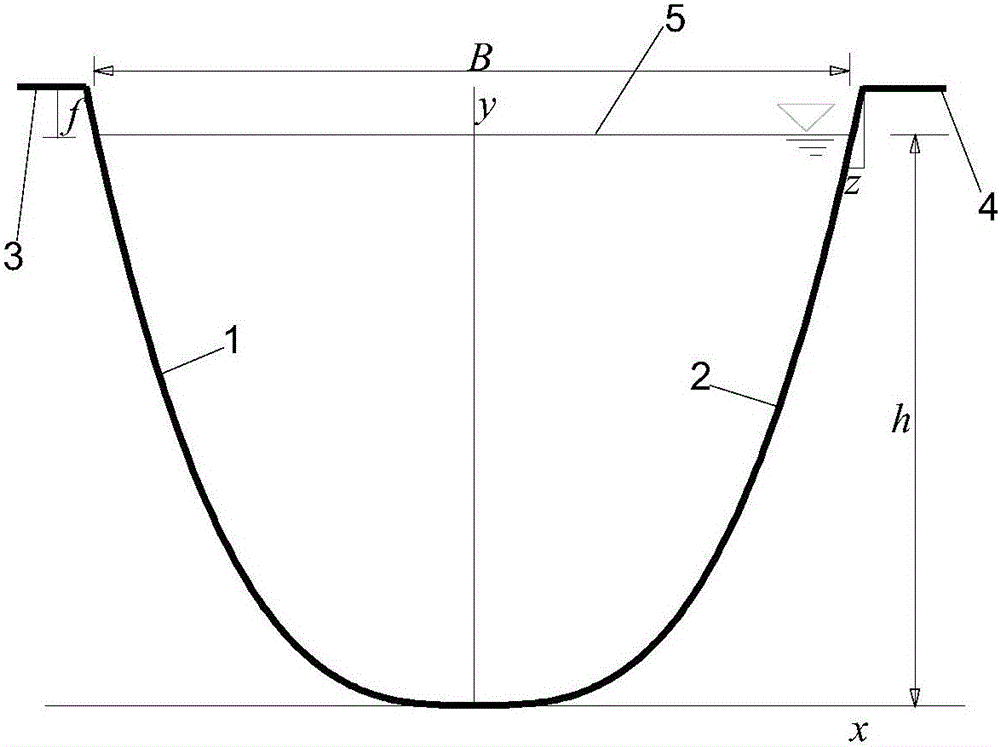
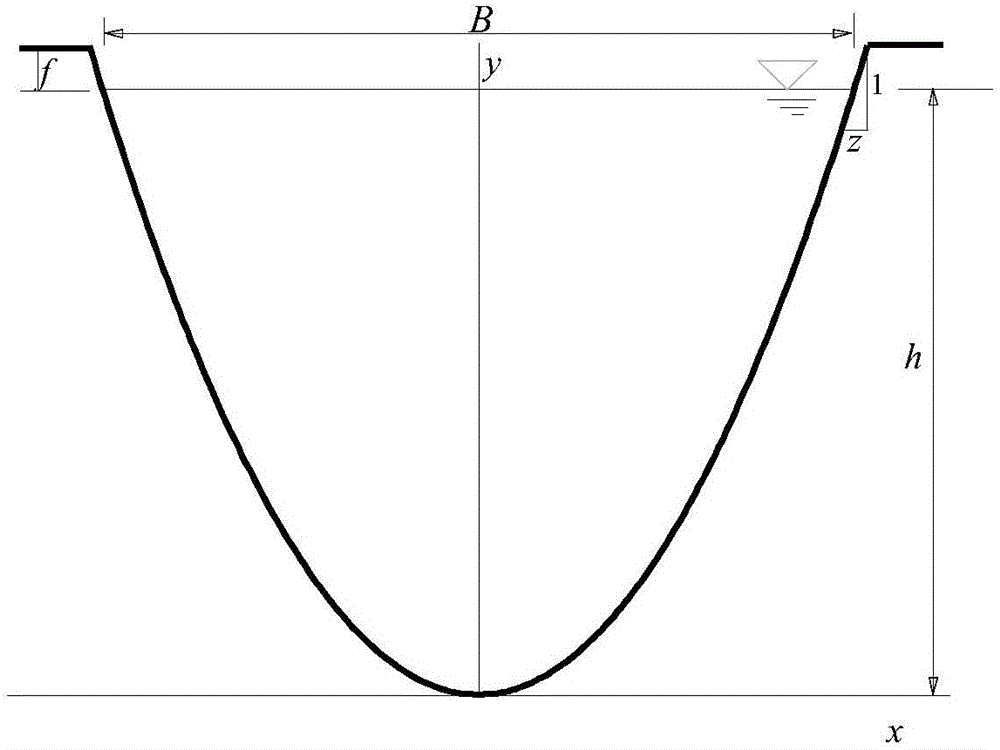
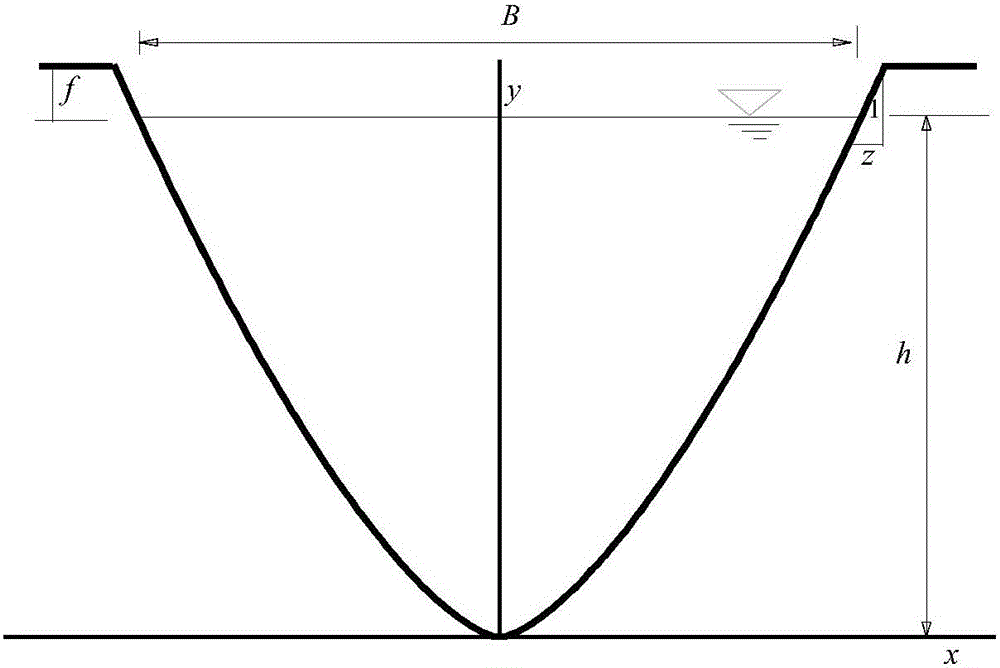
Waterpower optimal section of cubic parabola shaped water conveying open channel, and solving method for cubic parabola shaped waterpower optimal section
The invention discloses a cubic parabola shaped waterpower optimal section of a water conveying open channel, and a solving method for the cubic parabola shaped waterpower optimal section. The waterpower optimal section employs a cubic parabola shaped section, and is expressed as y=ax<3>, wherein the optimal width to depth ratio is B / h=2.1139, the shape coefficient a=0.8469h<-2>, and the side slope coefficient of a water surface is z=1 / 6* B / h=0.3523. The solving method comprises the steps: firstly designing the shape of the waterpower section of the water conveying open channel as the cubic parabola shaped waterpower section, and solving the characteristics of the waterpower section; secondly building a solving model for the waterpower optimal section; thirdly solving a differential equation of the waterpower optimal section through employing the Lagrangian multiplier method; fourthly enabling a wetted perimeter to be expressed as an expression of a complete elliptic integral function in a complex field range; and finally converting an optimal section problem into an equation with one unknown quantity in the complex field range, and obtaining the width to depth ratio of the waterpower optimal section. The waterpower optimal section is larger in discharge capacity under the condition of equal area or wetted perimeter, facilitates the improvement of the water conveying efficiency, and is low in construction cost.
Owner:UNIV OF JINAN
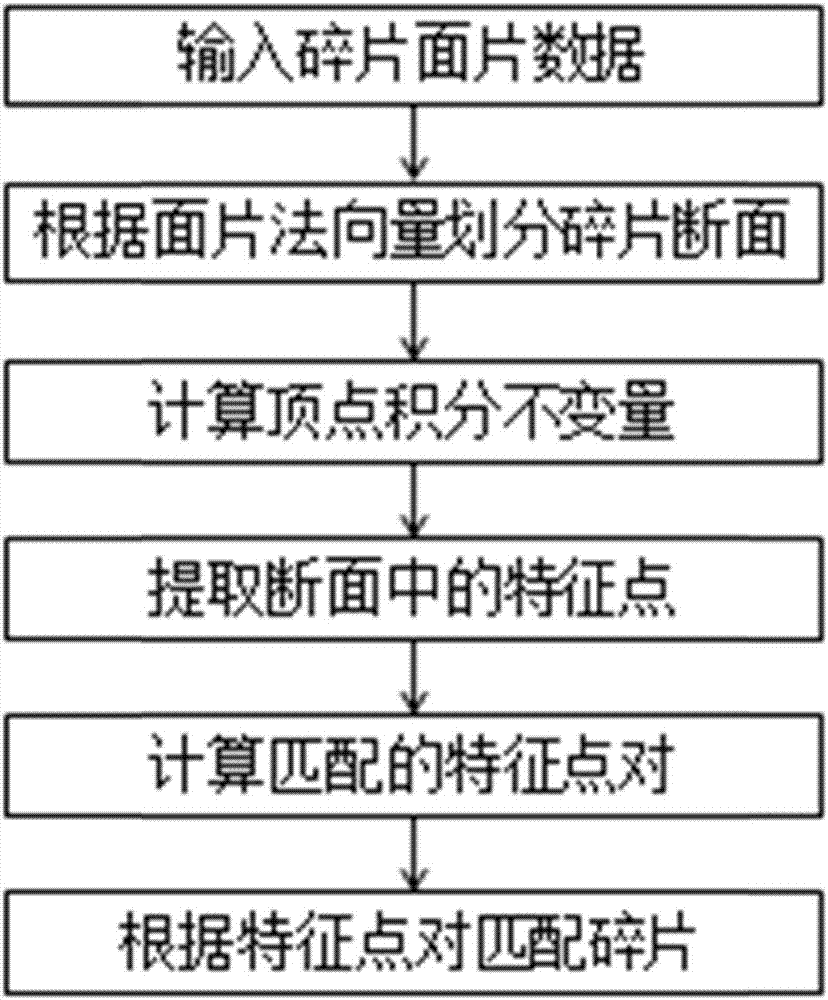
Automatic historical relic fragment splicing method
The invention discloses an automatic historical relic fragment splicing method. The method comprises steps that to-be-spliced historical relic fragments are scanned, and a three-dimensional model of each historical relic fragment is established; meshing of the three-dimensional model is carried out; surface division operation of the three-dimensional model is carried out, vertexes on a same smooth surface are divided into one group, and the vertexes contained by each smooth surface are acquired; an integral invariant of each vertex of the historical relic fragments is calculated; according to acquired sections and the integral invariant of each vertex, characteristic point pairs of each section having the equal integral invariants under a set threshold scope are acquired; a greedy algorithm is employed to acquire matching relationships of the fragments according to the characteristic pairs, and the historical relic fragments are spliced and matched according to the matching relationships.
Owner:DALIAN UNIV OF TECH
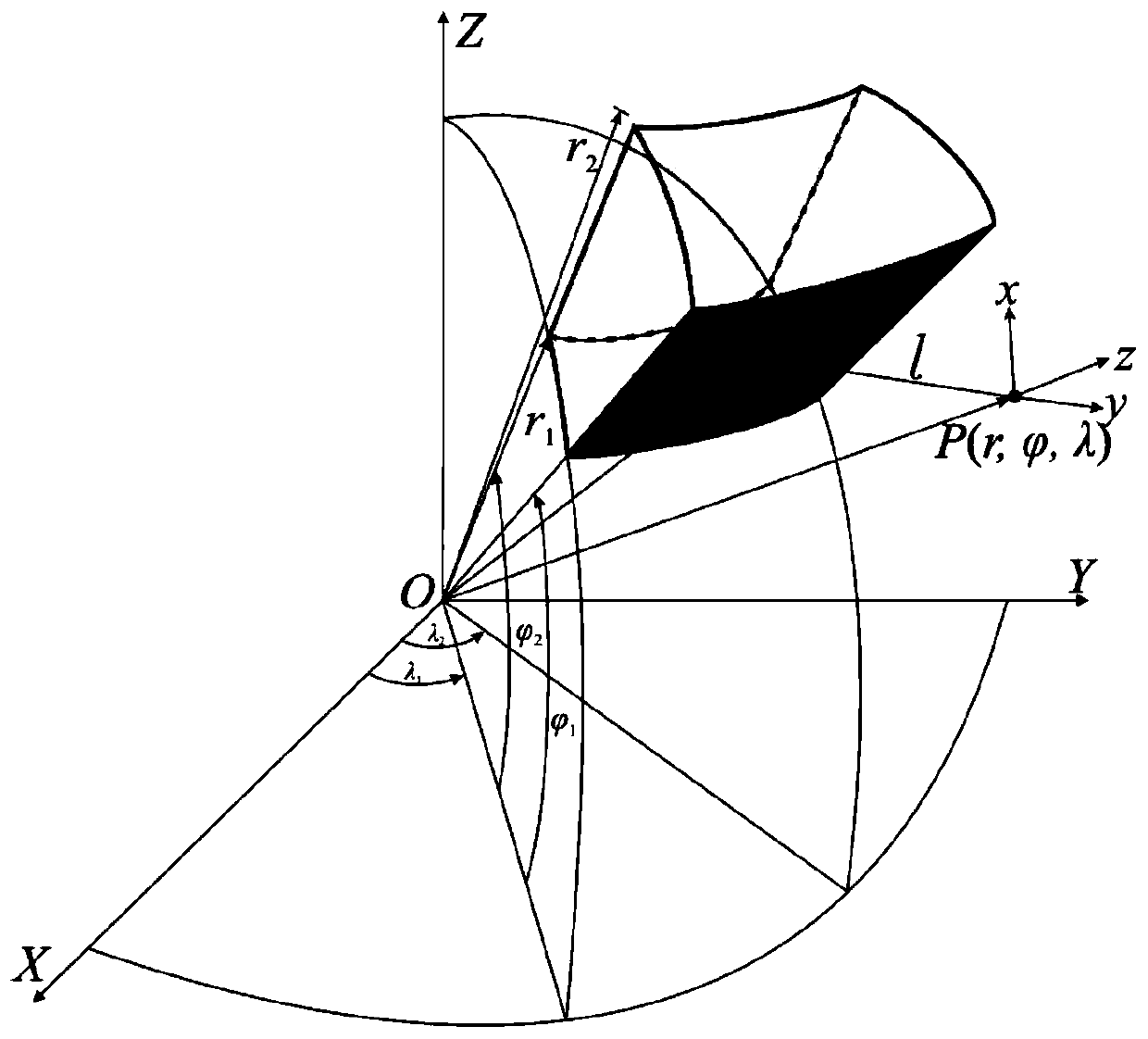
Gravity field forward modeling method and three-dimensional inversion method in spherical coordinate system based on 3D-GLQ
ActiveCN110045432AKernel Matrix Equivalence Relation SimplificationEquivalence relation simplificationGravitational wave measurementModel methodNuclear matrix
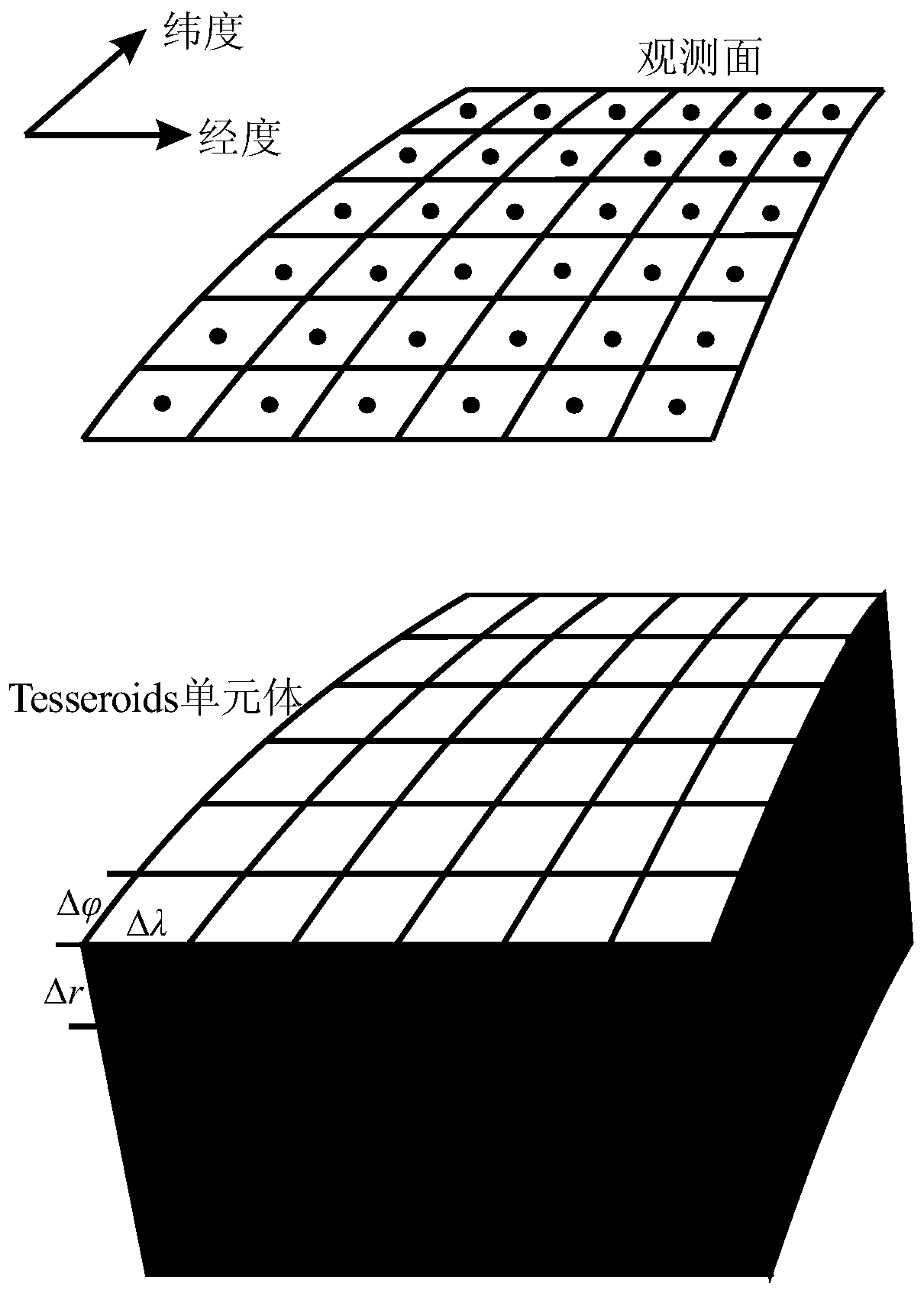
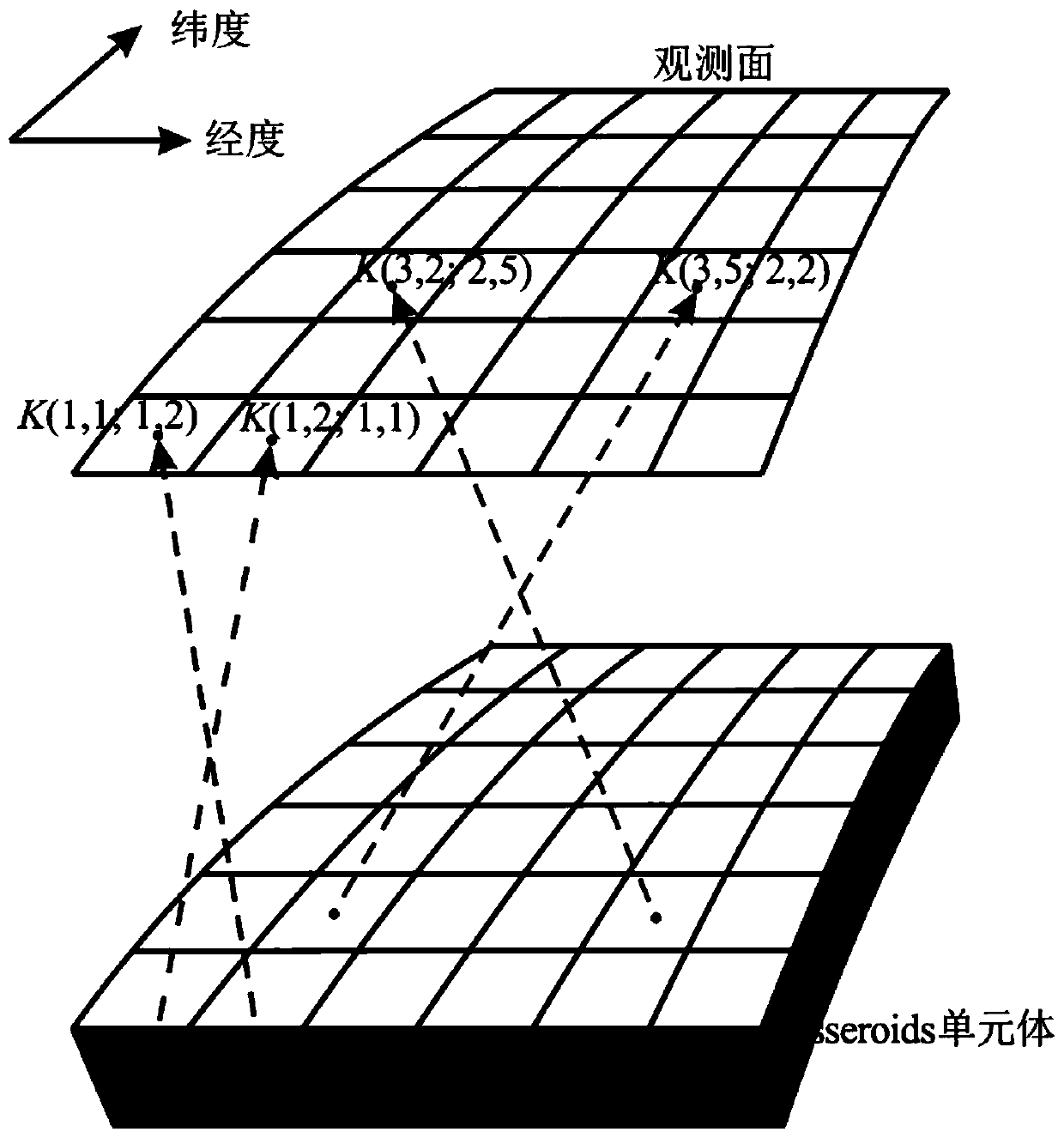
The application provides a three-dimensional gravity field fast and high-precision inversion algorithm in a spherical coordinate system based on a three-dimensional Gauss-legendre numerical integration formula (3D-GLQ). The core content comprises the following two points that the first point lies in the aspect of three-dimensional gravity field forward modeling in the spherical coordinate system,a nuclear matrix equivalent storage strategy is proposed aiming at the problem of low computational efficiency of the traditional 3D-GLQ three-dimensional gravity field forward modeling algorithm, thenuclear matrix equivalence is combined with the existing adaptive splitting strategy, the computational efficiency is increased by two orders of magnitude under the premise of ensuring that the maximum relative error of the forward modeling calculation is less than 0.1%, and the memory occupancy is greatly reduced at the same time; and the second point lies in that the above fast and high-precision forward modeling algorithm is applied to the gravity field three-dimensional inversion, and the gravity field inversion objective function and depth weighting function in the spherical coordinate system are constructed, so that the computational efficiency and credibility of the large-scale gravity field three-dimensional inversion in the spherical coordinate system are greatly improved.
Owner:CENT SOUTH UNIV
Sampling method
InactiveUS20060242217A1Increase sampleReduce probabilityDigital computer detailsDigital function generatorsState spaceDistribution function
The present invention is an incremental umbrella sampling method to improve the performance of established sampling methods. It is sampling the state space by iteratively generating states xi,t and their weighting factors represented by Formula (a) by fitting the sampling distribution function ρj(x) of the next iteration to at least one weighted property of the already sampled states. This means that ρj(x) is fitted to the product represented by Formula (b), in which Formula (a) is the weighting factor and O(x,i) is a function respectively a property of the states xi,t. The number of states xi,t and the number of weighting factors (see Formula (a)) is incremented with each iteration. In order to have a consistent set of weighting factors (see Formula (a)), the weighting factors are recalculated in each iteration for all, respectively for a set of selected, states. By fitting ρj(x) in the state space it is possible to use all the information of Formula (a) and O(xi,t) for the states xi,t generated so far. The fitting step allows to use different fitting strategies. For example the fitting can bias the sampling away from areas where intensive sampling has been done in the preceding iterations, or the sampling can be directed along local gradients respectively towards local minima or maxima of one or several weighted properties. In each of the iterations, the sampling distribution function is fitted in a way to improve the overall sampling of the state space. The method supports multi-objective optimisations. State space integrals can be solved. It reduces the probability that the system is trapped. The invention is general. It can be used with different sampling methods, in particular with Monte Carlo sampling, Metropolis Monte Carlo sampling, or dynamic simulations. It can be combined with the concepts of simulated annealing and multicanonical sampling. It provides a general framework that can be adapted to the system and the observables of interest.
Owner:BARTELS CHRISTIAN
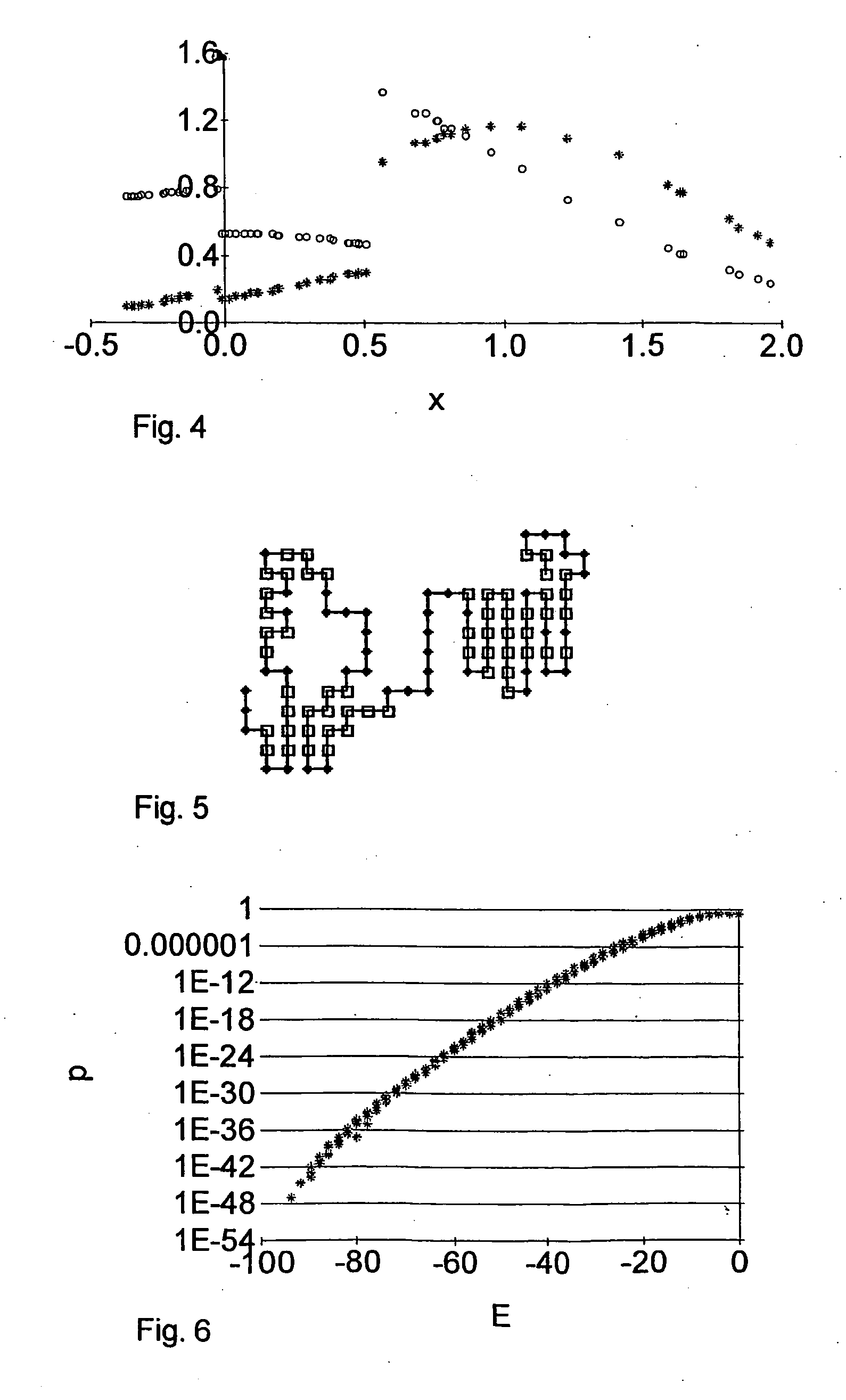
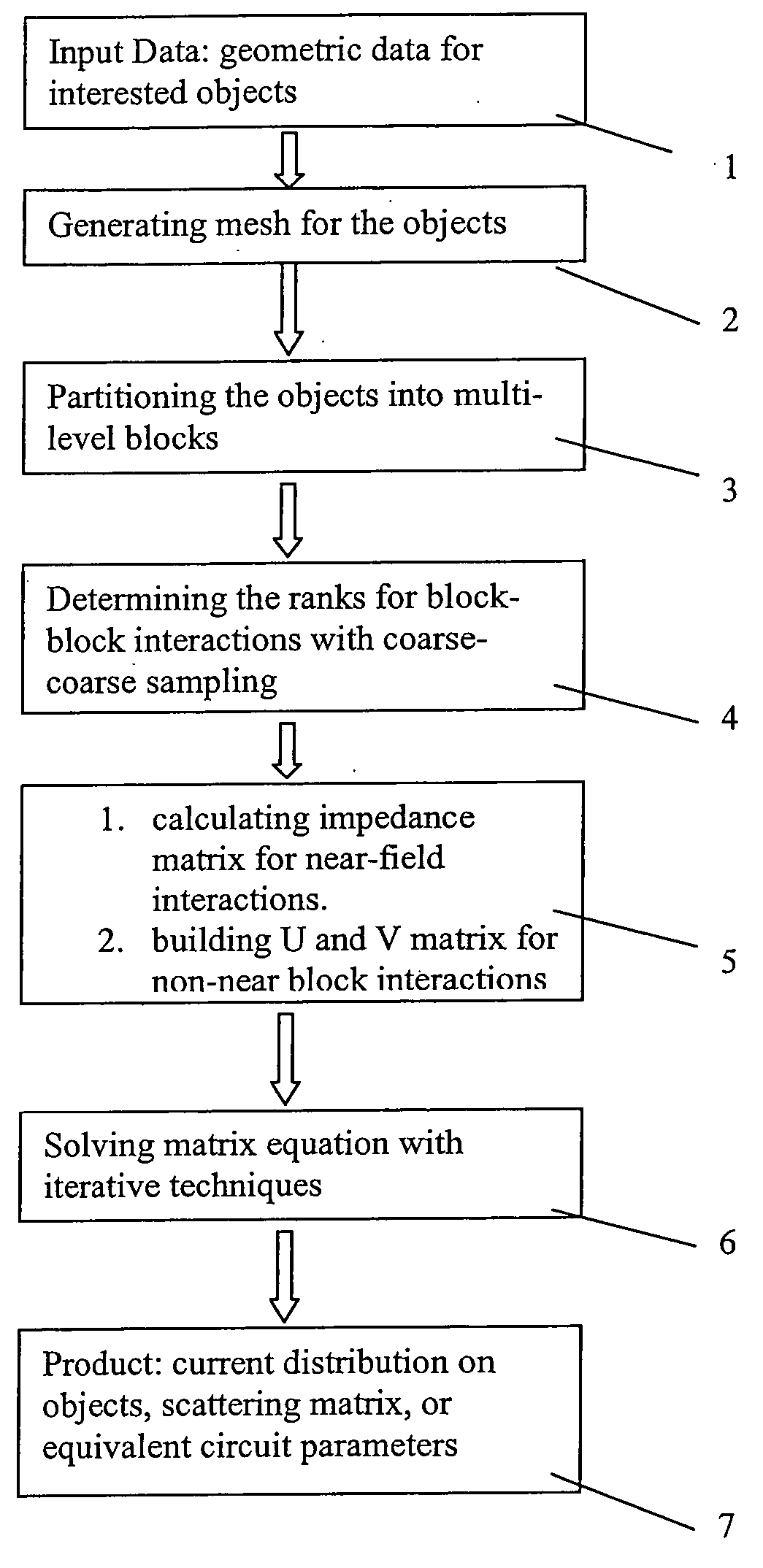
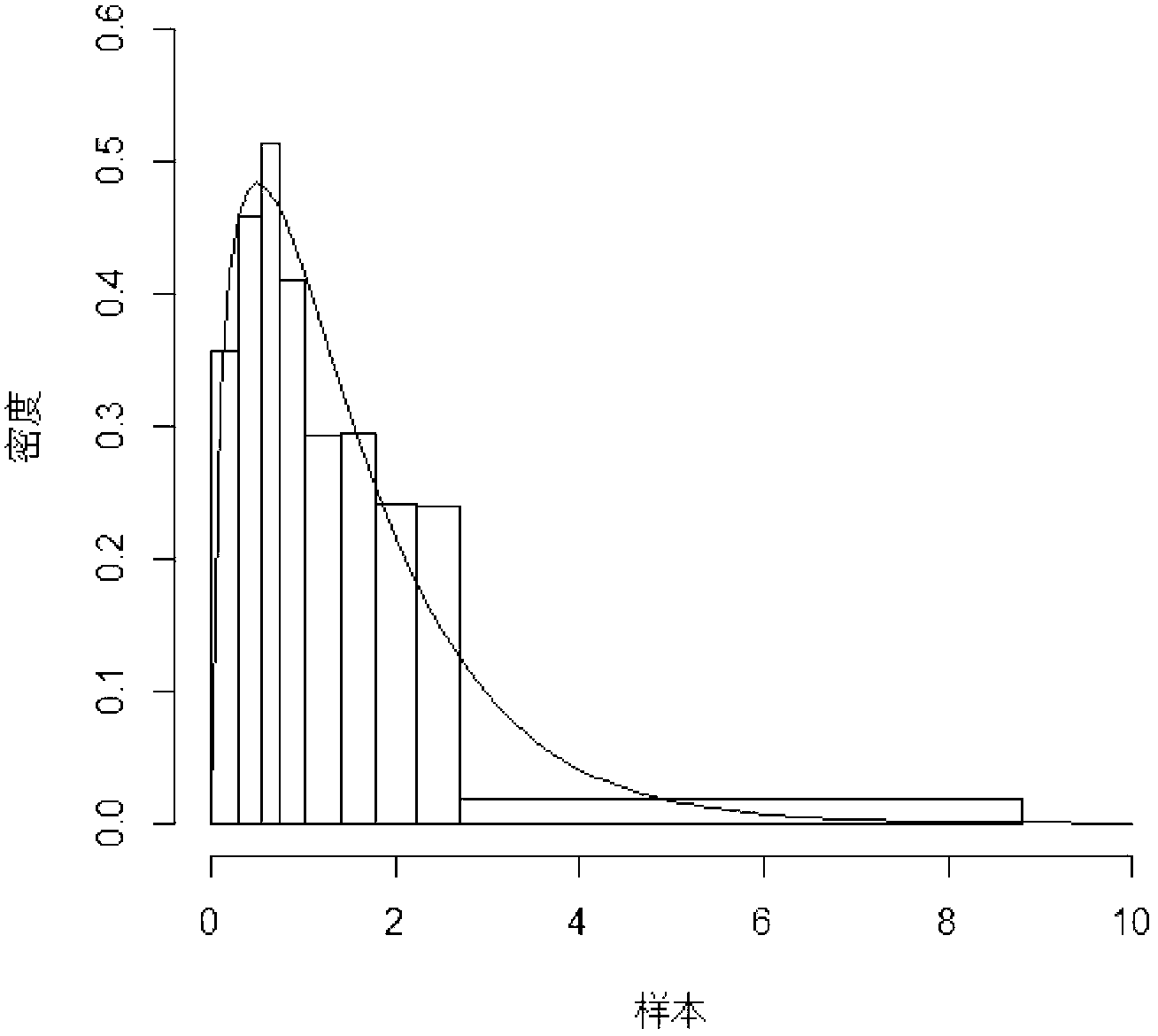
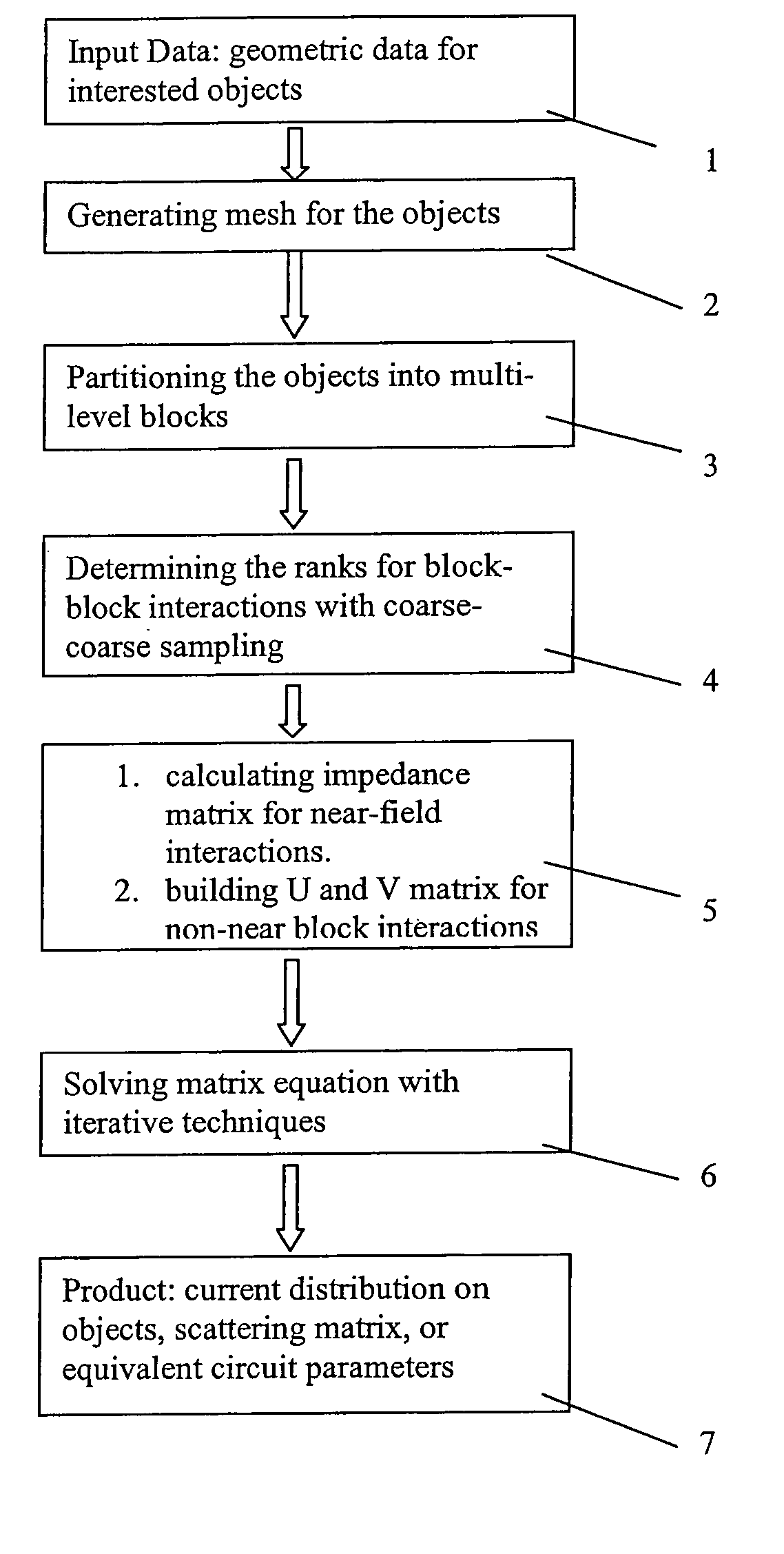
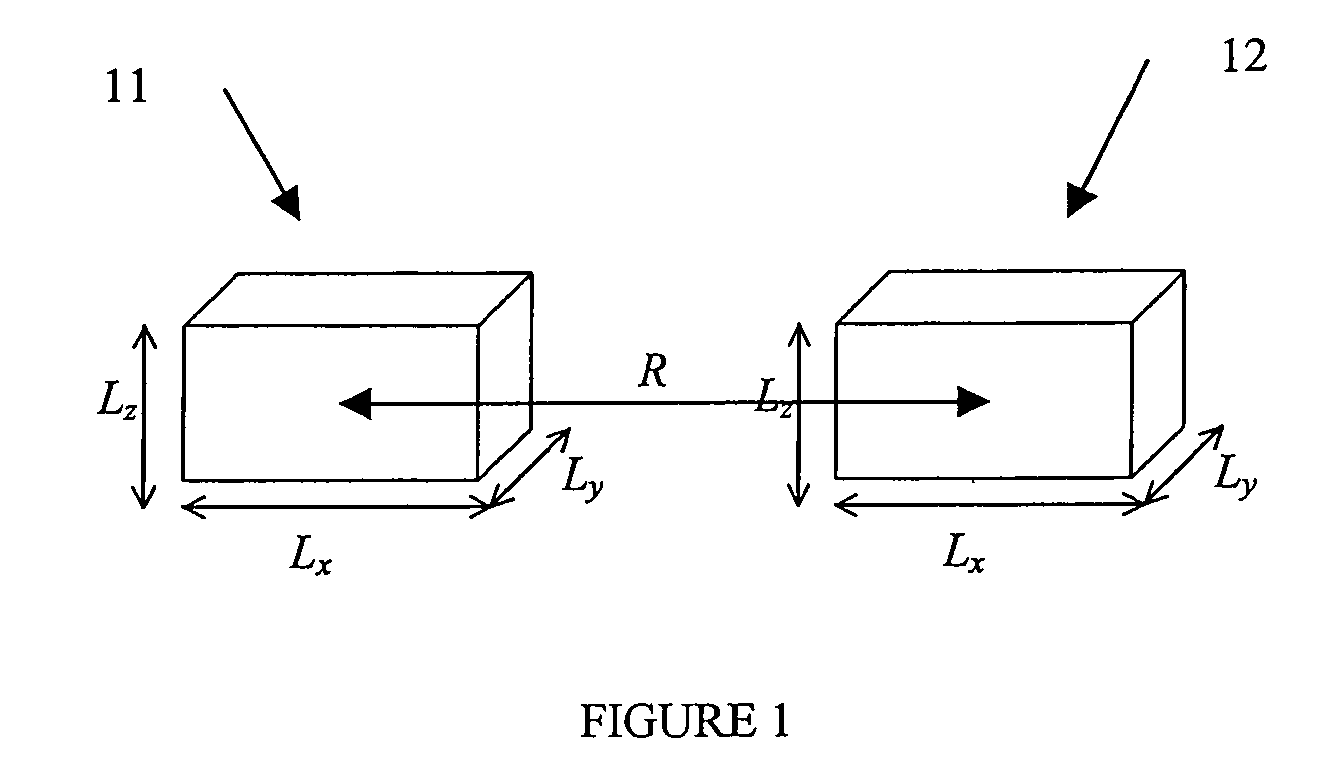
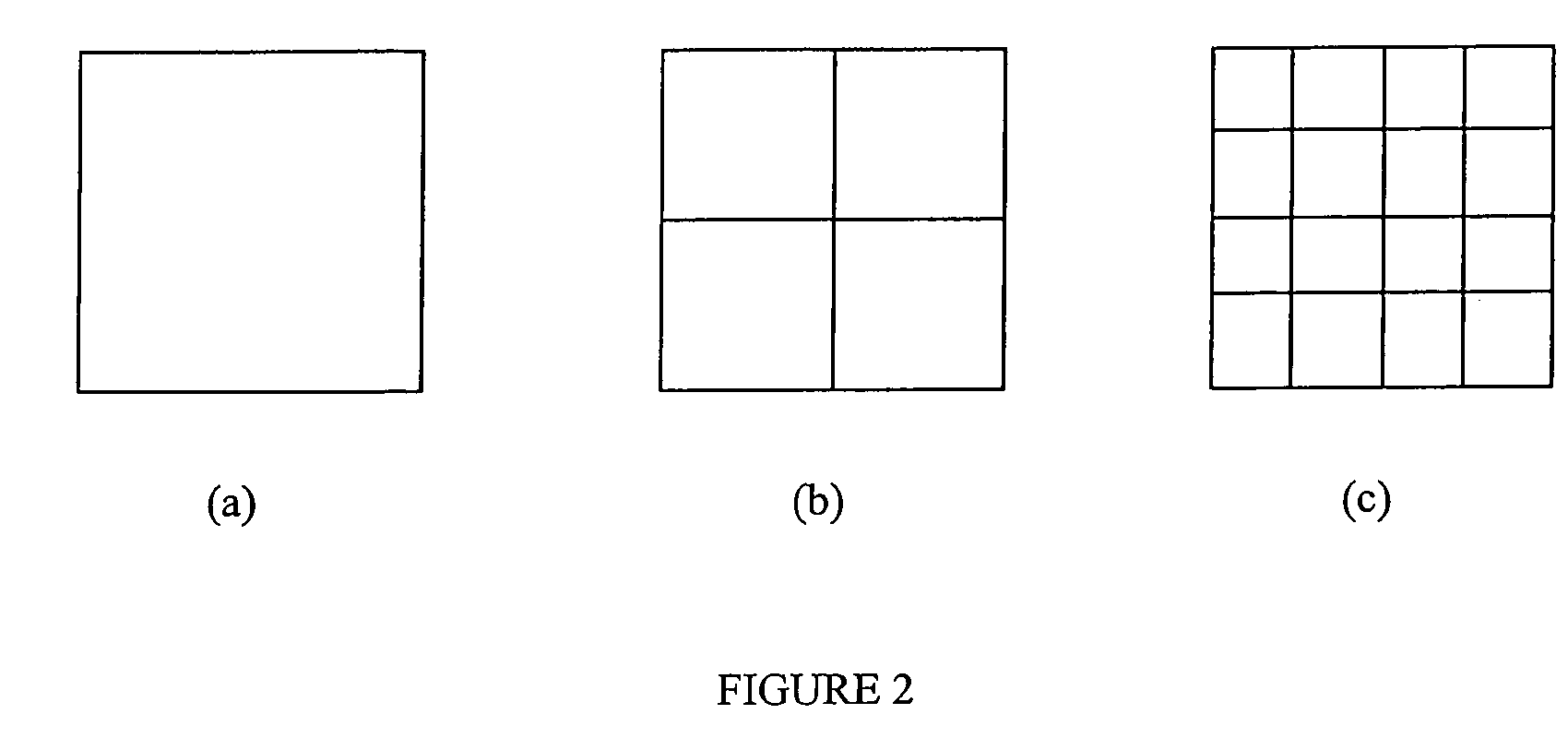
Fast solution of integral equations representing wave propagation
InactiveUS20050102343A1Effective applicationReduce in quantityDesign optimisation/simulationSpecial data processing applicationsWave equationClassical mechanics
A technique for solving a set of wave equations in a region uses points arranged in a grid spanning the region or coefficients of wave expansion for objects located in the region. The grid points or the coefficients are partitioned into blocks on multiple levels, and block impedance matrices encoding the wave equations is derived for pairs of blocks. The block impedance matrix need not be calculated as it is written as the product of two non-square matrices, denoted U and V. Each of U and V have one linear dimension which is only of the order of the rank of the block impedance matrix levels. The rank is predetermined by coarse sampling. Two examples of the use of the invention are given: solving surface integral equations and Foldy Lax equations for partial waves.
Owner:CITY UNIVERSITY OF HONG KONG
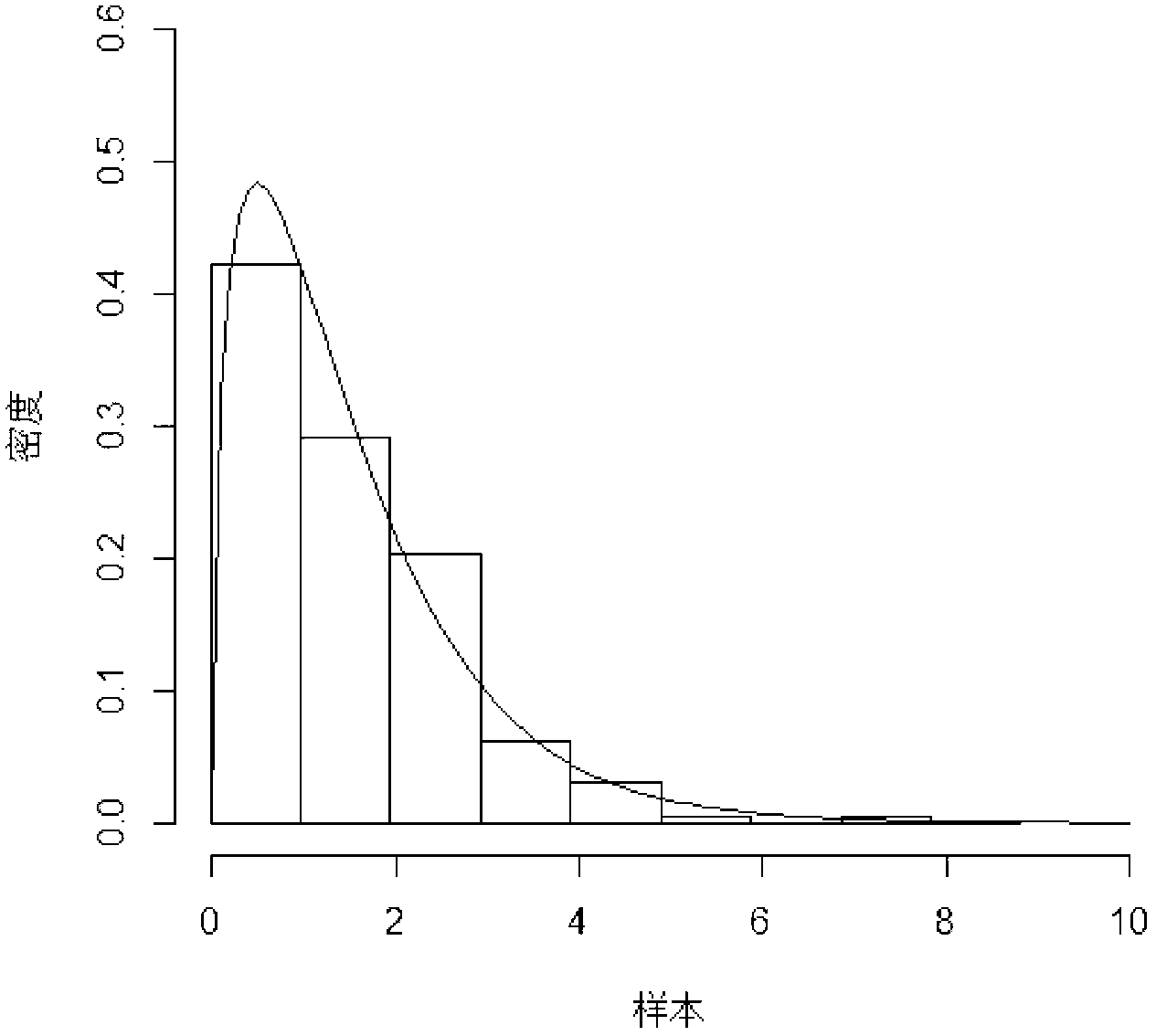
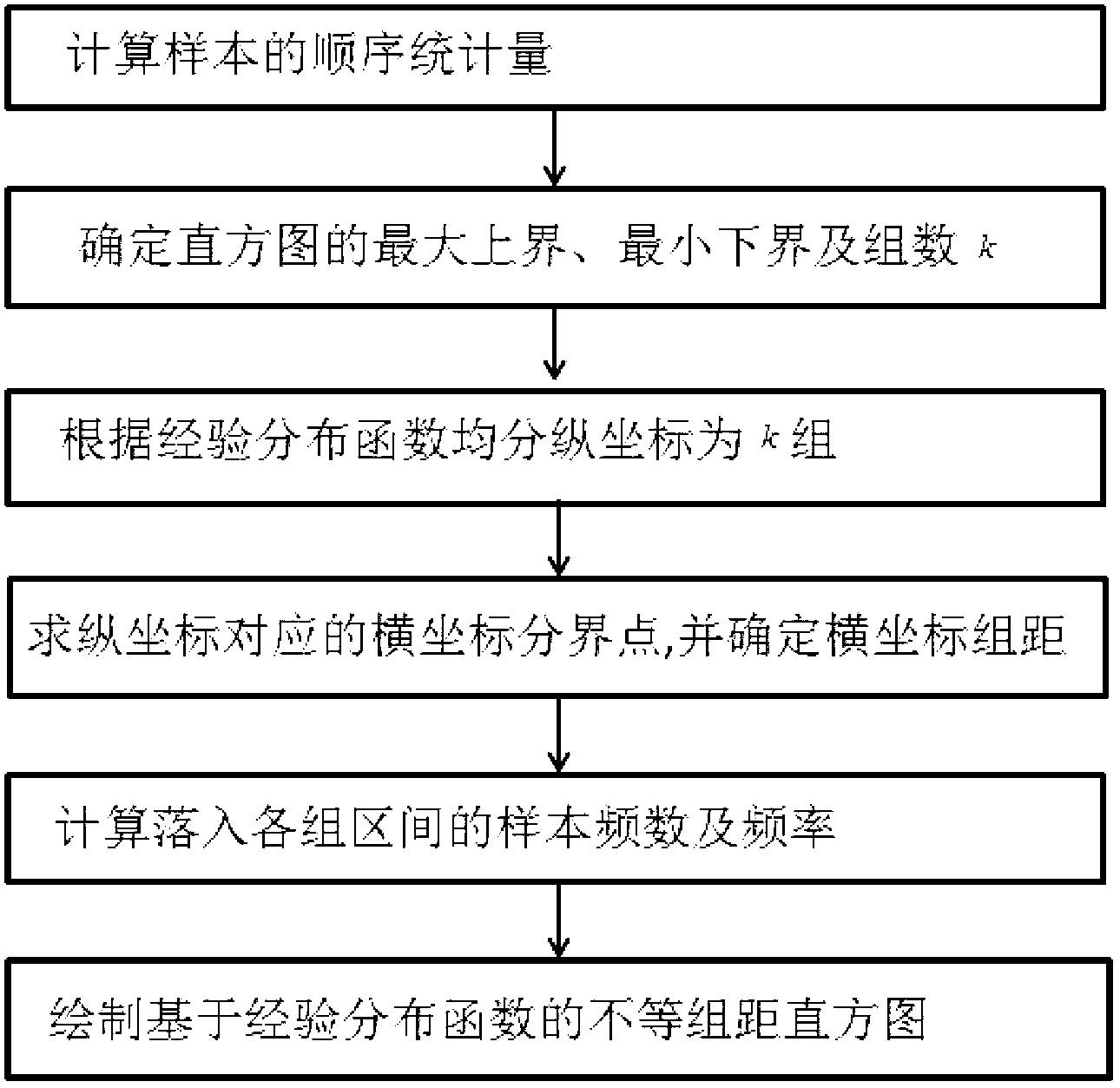
Unequal class interval histogram rendering method based on empirical distribution function
The invention provides an unequal class interval histogram rendering method based on an empirical distribution function. Aiming at the fact that an equal class interval histogram can not reflect distribution characteristics of a sample adequately, the distribution characteristics of the sample reflected by the equal class interval histogram is inconsistent with an actual situation, and the unequal class interval histogram rendering method based on the empirical distribution function is brought out by means of the property that the empirical distribution function is effective fitting of a distribution function. The rendering method includes the specific steps: 1, computing order statistic of the sample; 2, confirming maximum upper bond, minimum lower bond and class count k of a histogram; 3, dividing a vertical coordinate into k classes equally according to the empirical distribution function; 4, calculating demarcation points, corresponding to k classes of vertical coordinates, of a horizontal coordinate, confirming class intervals of k classes of horizontal coordinates; 5, computing frequency number and frequency of the sample dropping in each class interval; and 6, rendering the unequal class interval histogram based on the empirical distribution function. By means of a graphic method and comparative mean integrated square error (MISE), the histogram rendered through the unequal class interval histogram rendering method based on the empirical distribution function is testified to have an accurate fitting effect.
Owner:BEIHANG UNIV
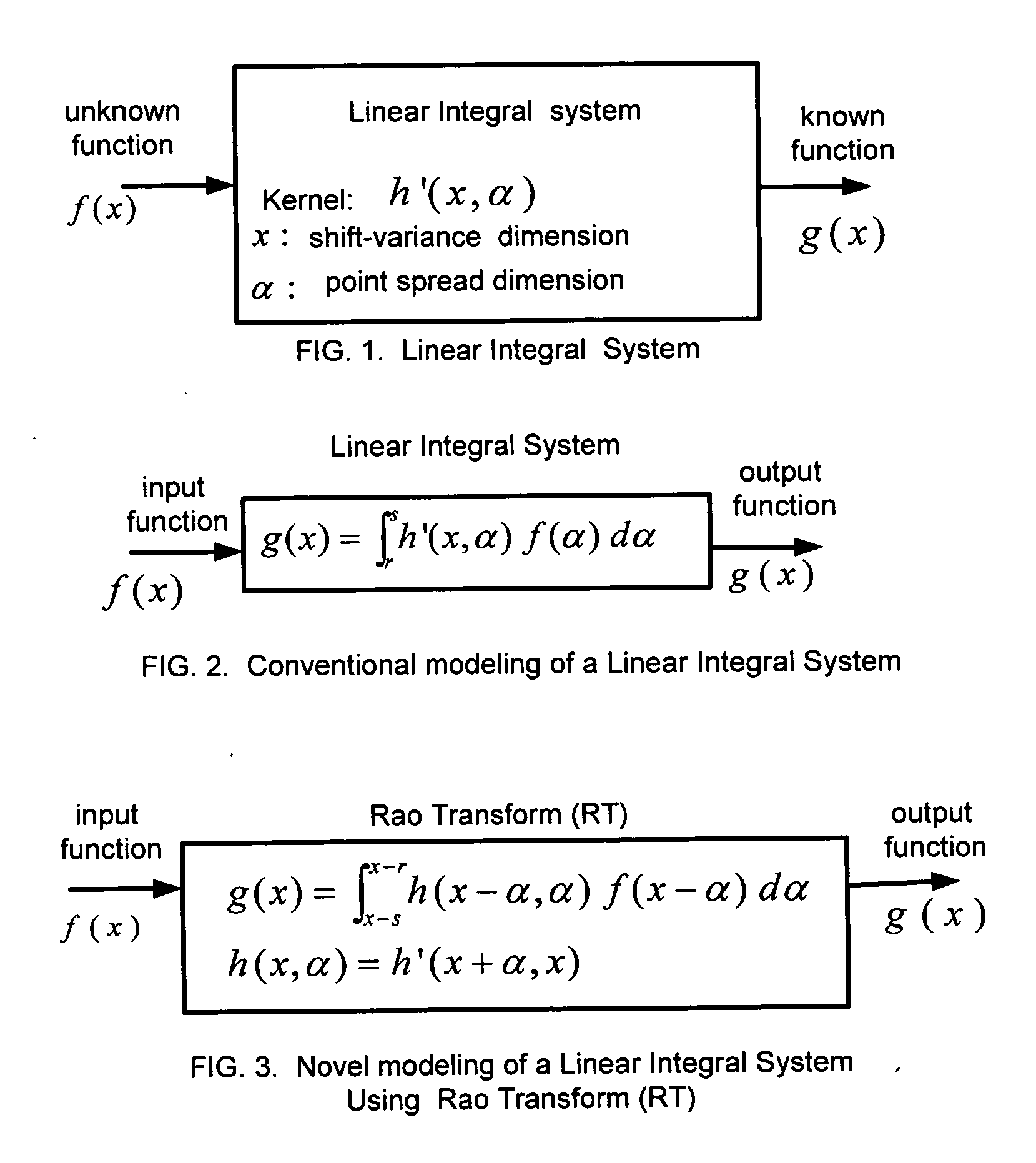
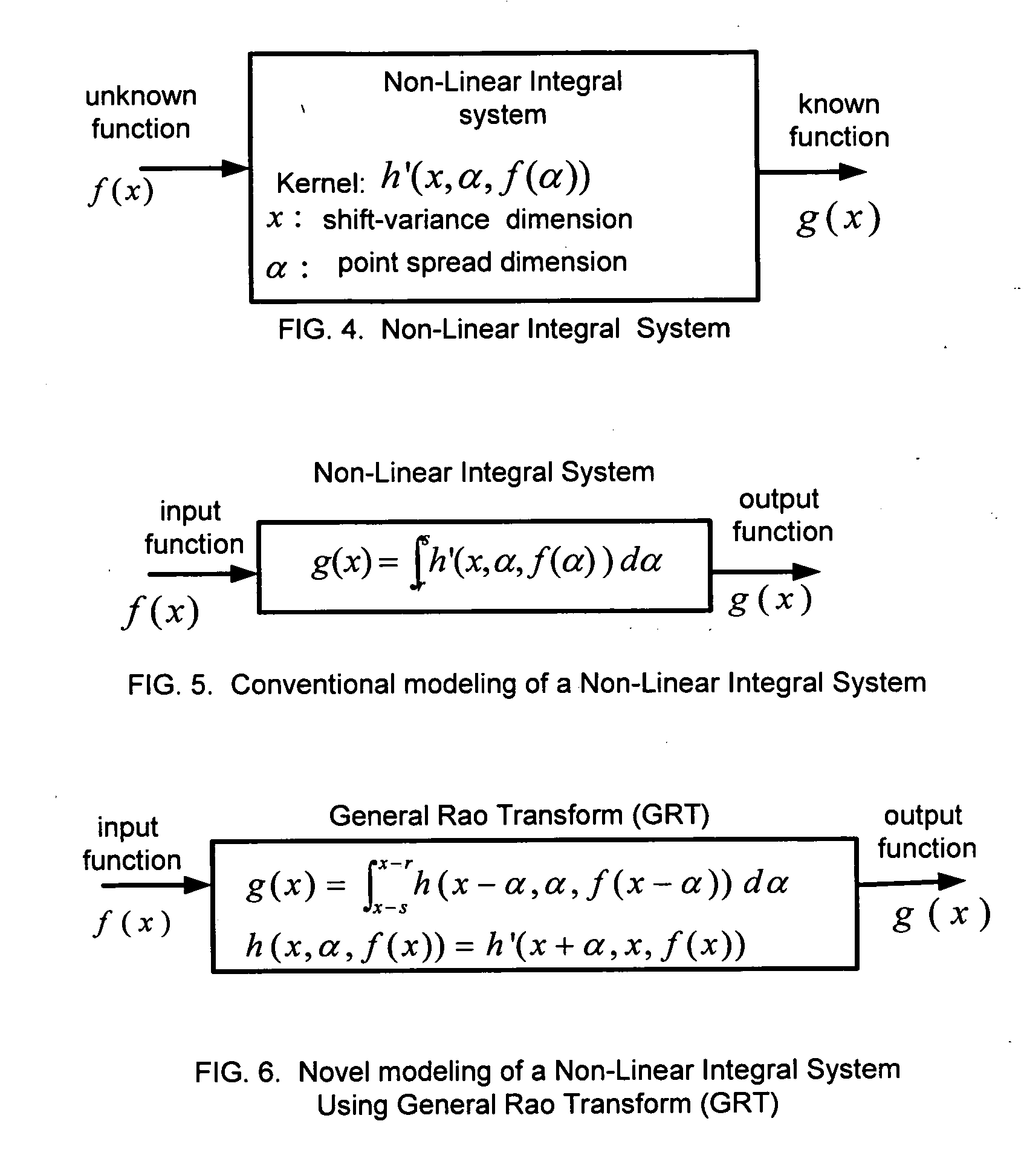
Unified and localized method and apparatus for solving linear and non-linear integral, integro-differential, and differential equations
InactiveUS20060111882A1Efficiently compute valueComplete efficientlyComputation using non-denominational number representationComplex mathematical operationsAlgorithmDifferential of a function
This invention is based on a new class of mathematical transforms named Rao Transforms invented recently by the author of the present invention. Different types of Rao Transforms are used for solving different types of linear / non-linear, uni-variable / multi-variable integral / integro-differential equations / systems of equations. Methods and apparatus that are unified and computationally efficient are disclosed for solving such equations. These methods and apparatus are also useful in solving ordinary and partial differential equations as they can be converted to integral / integro-differential equations. The methods and apparatus of the present invention have applications in many fields including engineering, science, medicine, and economics.
Owner:SUBBARAO MURALIDHARA
Weighted conserved variable step-based high-precision discontinuous Galerkin artificial viscosity shock wave capturing method
ActiveCN108197072AGuaranteed robustnessGuaranteed calculation accuracyDesign optimisation/simulationComplex mathematical operationsShock waveComputer science
The invention discloses a weighted conserved variable step-based high-precision discontinuous Galerkin artificial viscosity shock wave capturing method. according to the method, an unstructured grid is adopted to subdivide a calculation area; an Euler equation is adopted as a control equation; a DG high-precision framework which takes a primary function, a test function and a Gauss integral pointas representatives is established; on the equation, a new artificial conserved variable step-based high-precision discontinuous Galerkin artificial viscosity term is constructed by taking a step of conserved variable on a unit interface; and a convective term of the equation is discretely solved by adoption of an HLL format, so that the robustness and calculation precision are ensured under the condition of effectively capturing shock waves. Compared with past methods, the method only needs one experience parameter, so that the practical calculation is simplified; step amounts of conversed variables are adopted to carry out calculation; and compared with past methods, the method is capable of ensuring compatibility in smooth areas, so that the shock wave capturing positions are more correct than that of the past methods.
Owner:CALCULATION AERODYNAMICS INST CHINA AERODYNAMICS RES & DEV CENT
Fully bayesian linear regression
ActiveUS7565334B2Prevent overfittingDigital computer detailsDigital dataHyperparameterComputer science
A simple yet powerful Bayesian model of linear regression is disclosed for methods and systems of machine learning. Unlike previous treatments that have either considered finding hyperparameters through maximum likelihood or have used a simple prior that makes the computation tractable but can lead to overfitting in high dimensions, the disclosed methods use a combination of linear algebra and numerical integration to work a full posterior over hyperparameters in a model with a prior that naturally avoids overfitting. The resulting algorithm is efficient enough to be practically useful. The approach can be viewed as a fully Bayesian version of the discriminative regularized least squares algorithm.
Owner:HONDA MOTOR CO LTD
Fast solution of integral equations representing wave propagation
InactiveUS7359929B2Quick fixIncrease in sizeDesign optimisation/simulationSpecial data processing applicationsWave equationClassical mechanics
A technique for solving a set of wave equations in a region uses points arranged in a grid spanning the region or coefficients of wave expansion for objects located in the region. The grid points or the coefficients are partitioned into blocks on multiple levels, and block impedance matrices encoding the wave equations is derived for pairs of blocks. The block impedance matrix need not be calculated as it is written as the product of two non-square matrices, denoted U and V. Each of U and V have one linear dimension which is only of the order of the rank of the block impedance matrix levels. The rank is predetermined by coarse sampling. Two examples of the use of the invention are given: solving surface integral equations and Foldy Lax equations for partial waves.
Owner:CITY UNIVERSITY OF HONG KONG
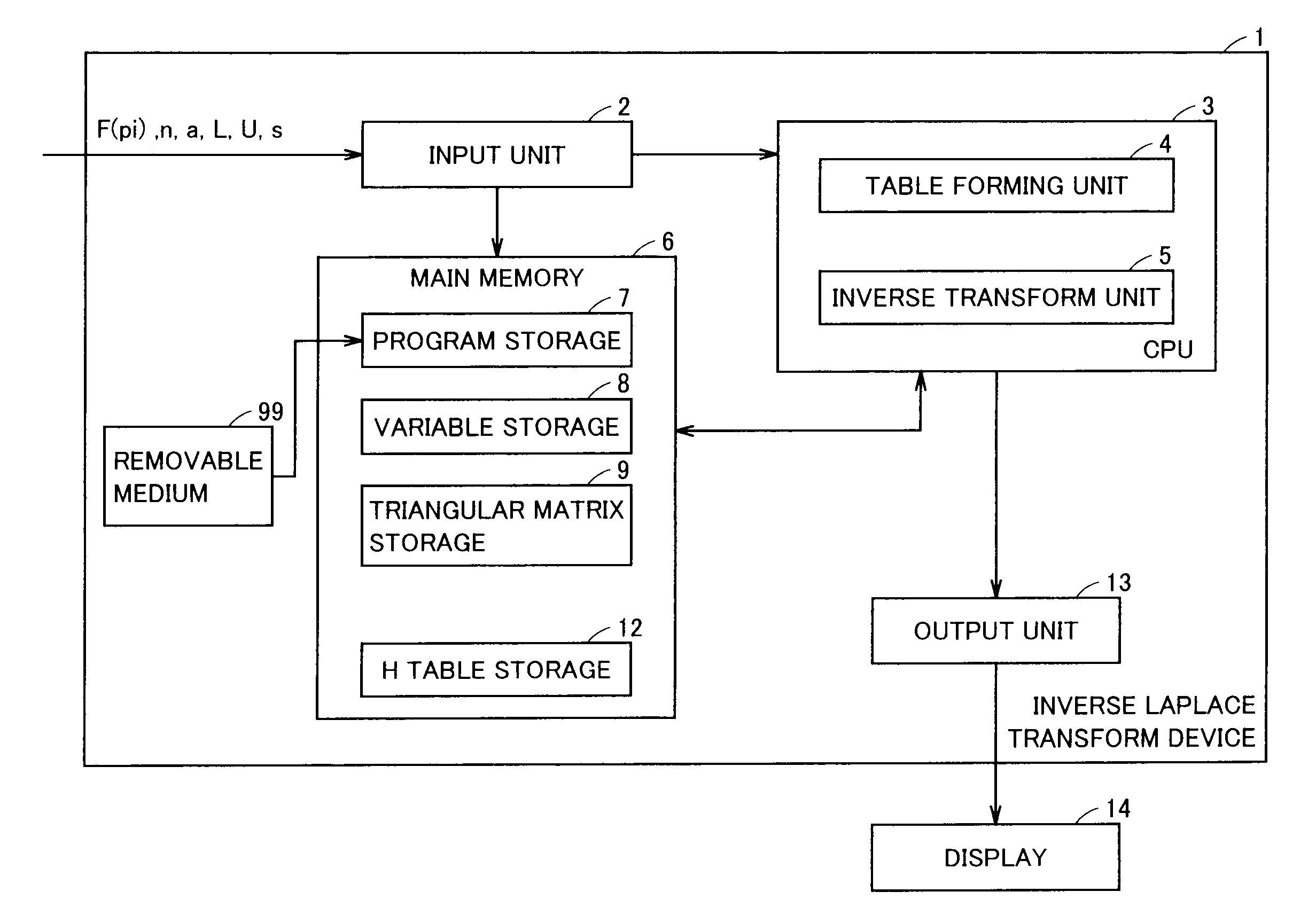
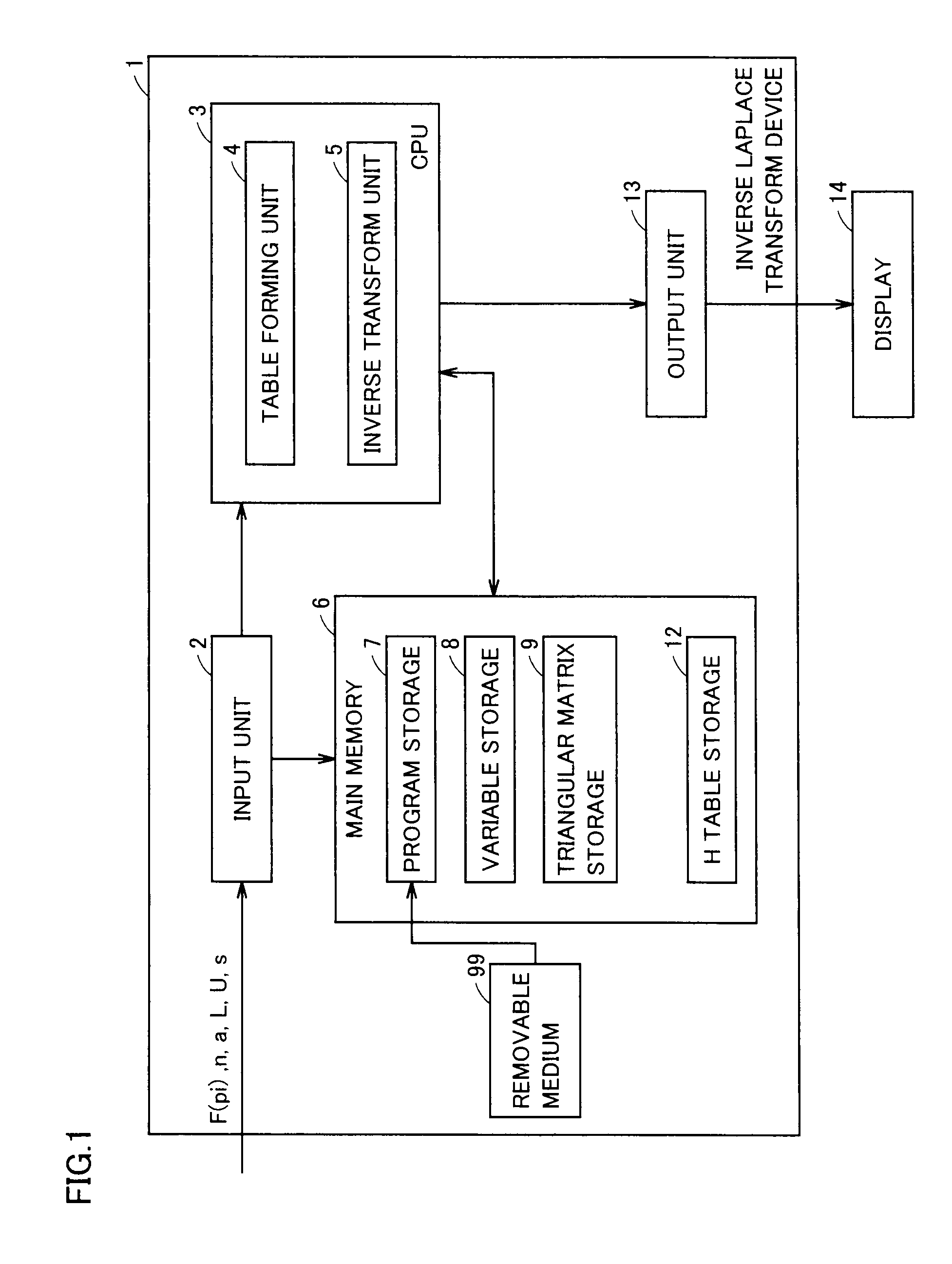
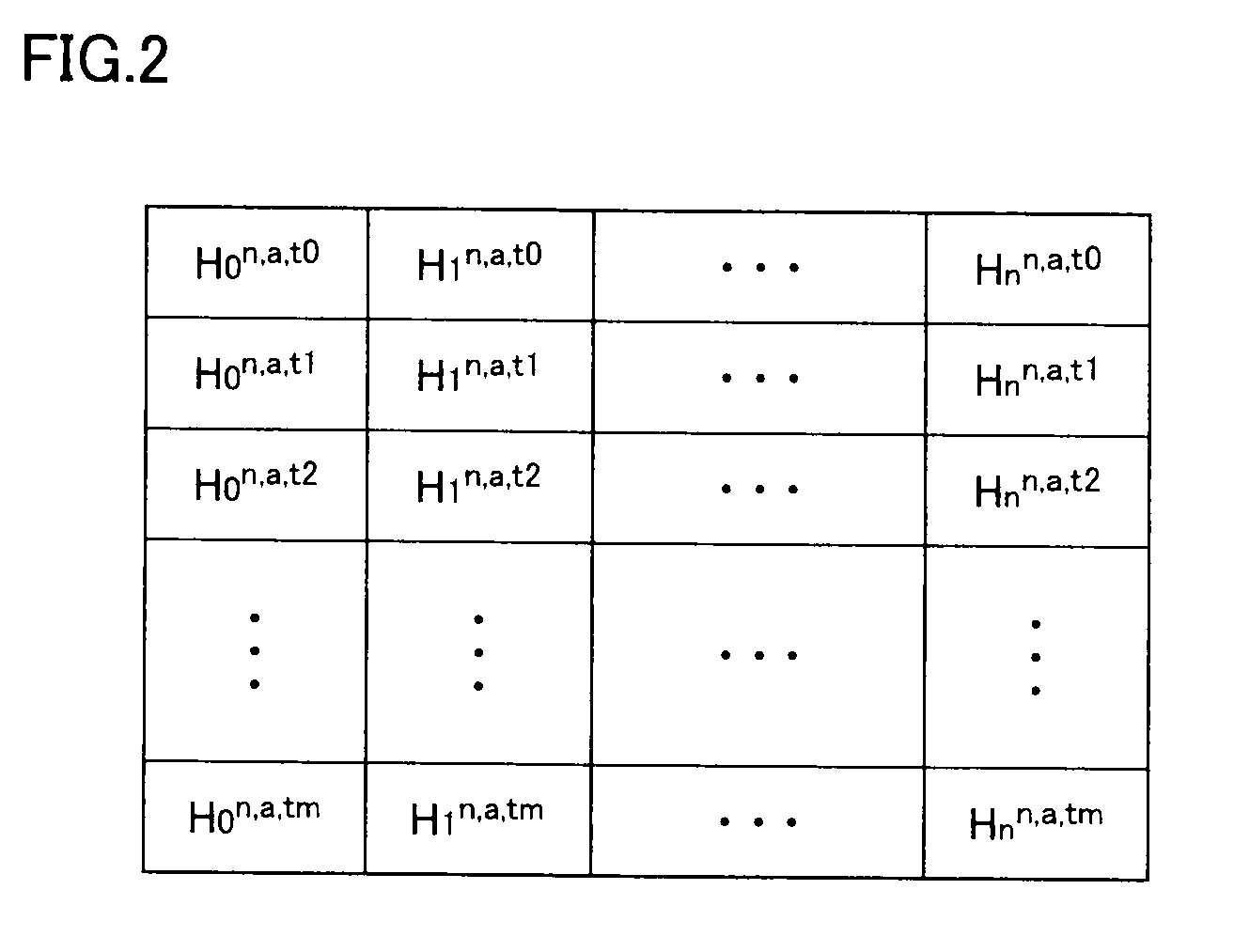
Inverse laplace transform program, program for forming table for inverse laplace transform, program for calculating numerical solution of inverse laplace transform, and inverse laplace transform device
InactiveUS20100268753A1Possible to calculateComplex mathematical operationsSimultaneous equationsReproducing kernel Hilbert space
A table forming unit calculates, in a weighted reproducing kernel Hilbert space formed of an absolutely continuous function that is zero at an origin, solutions of simultaneous equations obtained by discretization of an integral equation of the second kind derived from Tikhonov regularization method with a weighted square integrable space used as an observation space, and forms an H table describing information including numerical solution of the integral equation of the second kind based on the solutions of the simultaneous equations. An inverse transform unit obtains, by numerical calculation, an inner product, in the weighted square integrable space, of the numerical solution of the integral equation of the second kind and a Laplace transform image multiplied by a mollifier function with reference to the H table.
Owner:KYOTO UNIV +1
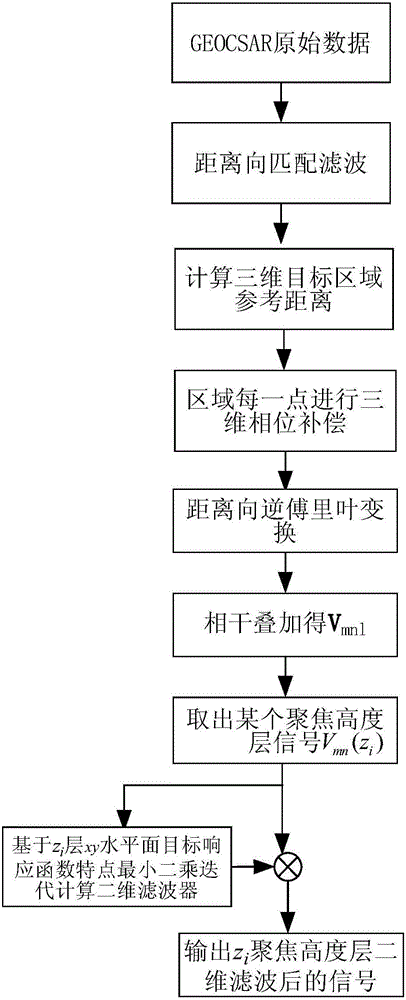
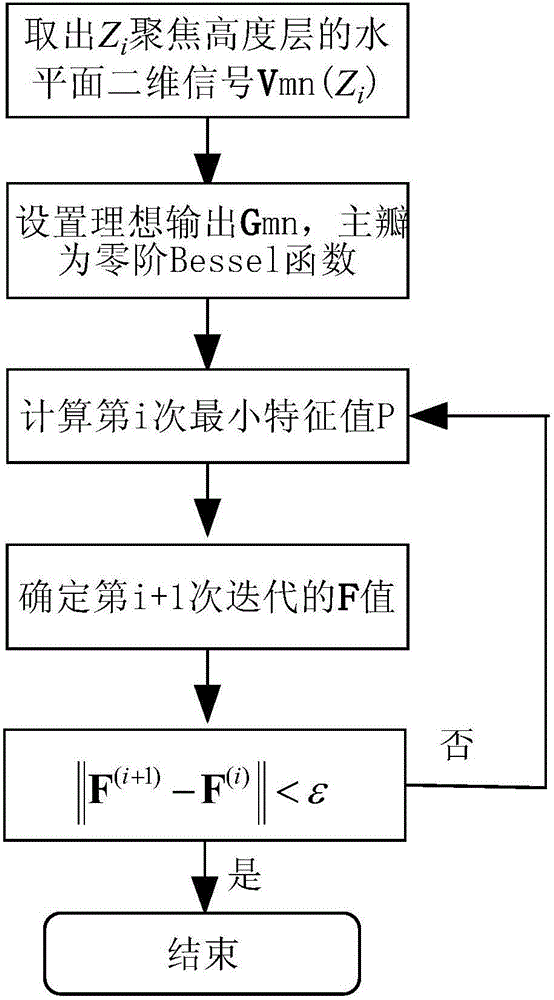
Method for suppressing two-dimensional side lobes on horizontal planes for geosynchronous orbit circular SAR (synthetic aperture radar)
ActiveCN106772276AGood interference effectNo loss of resolutionRadio wave reradiation/reflectionTarget ResponseSynthetic aperture sonar
The invention discloses a method for suppressing two-dimensional side lobes on horizontal planes for geosynchronous orbit circular SAR (synthetic aperture radar), and belongs to the field of synthetic aperture radar (SAR) signal processing. The method has the advantages that the method is based on characteristics of geosynchronous orbit circular SAR three-dimensional imaging target response functions, two-dimensional side lobe suppression filter functions can be obtained on the basis of confocal algorithms by the aid of total least squares iterative processes, and accordingly the two-dimensional high side lobes on the horizontal planes can be suppressed for the geosynchronous orbit circular SAR; the two-dimensional horizontal high side lobes can be effectively diminished (peak side lobe ratios can be reduced from the original -7.9 dB to -20 dB approximately, and integration side lobe ratios can be reduced from the original -4.79 dB to -20 dB approximately) for the geosynchronous orbit circular SAR by the aid of the method without loss of resolution, and accordingly the imaging and interference performance of the geosynchronous orbit circular SAR can be improved.
Owner:NANJING UNIV OF INFORMATION SCI & TECH
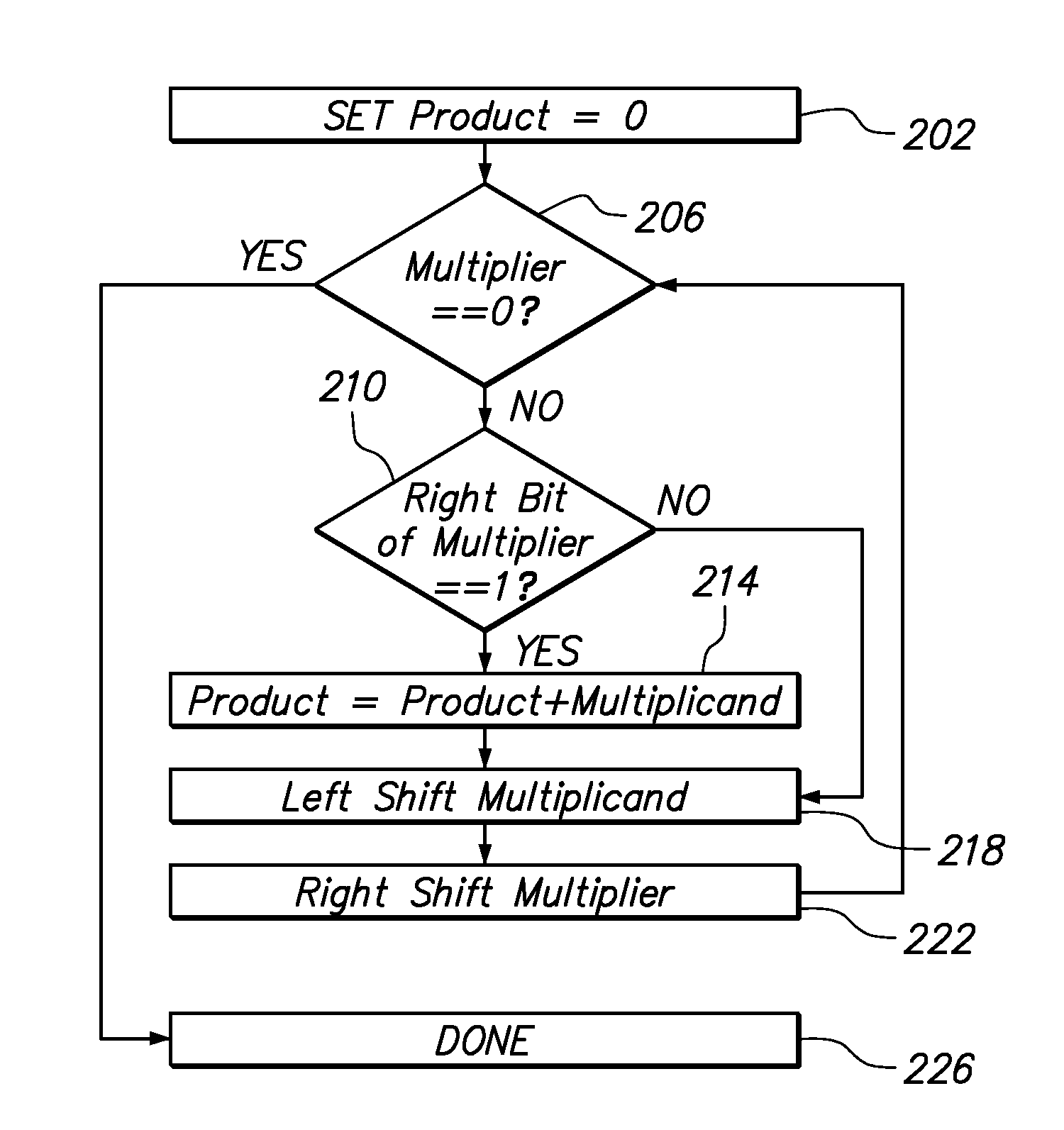
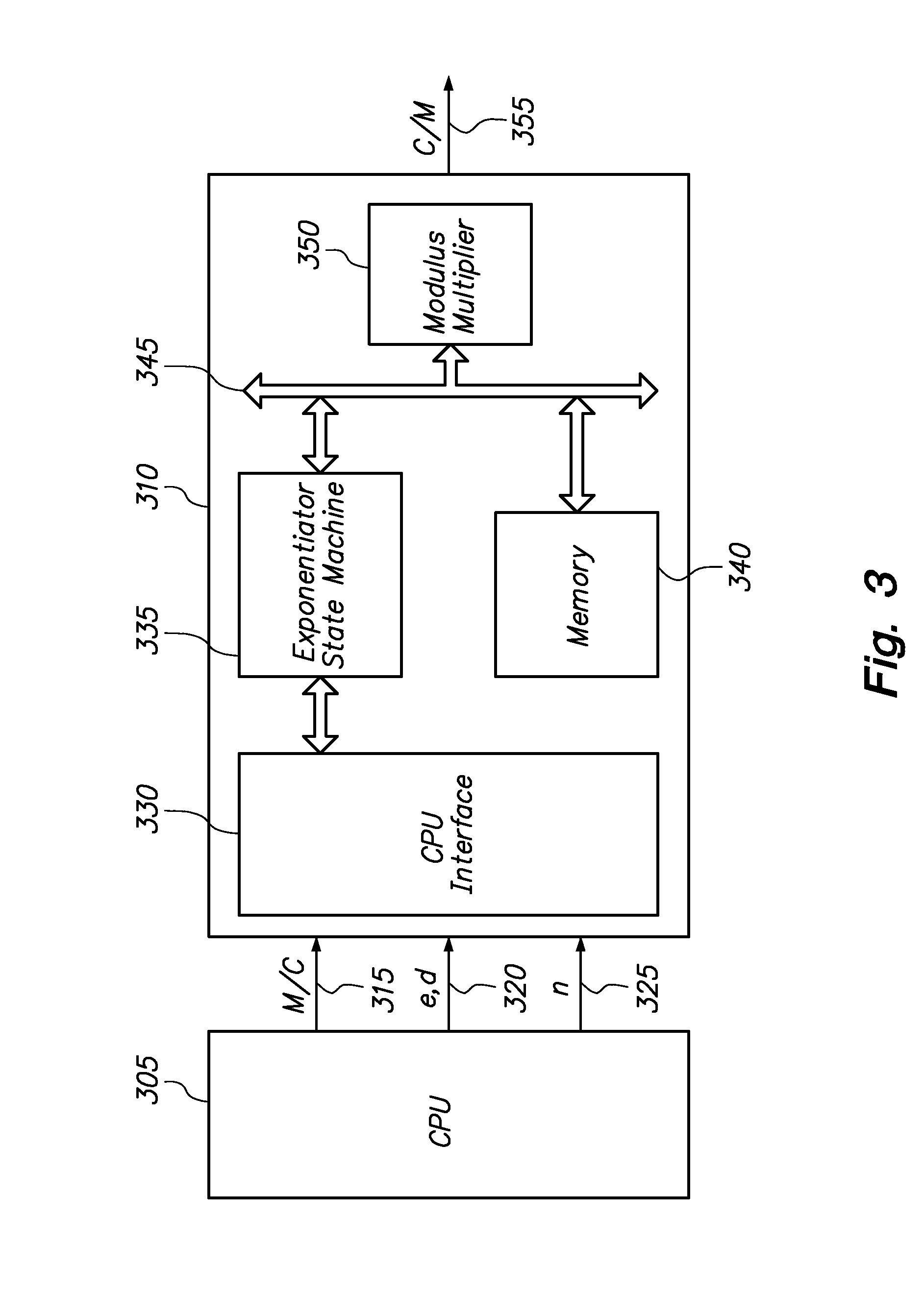
System and Method for Modular Exponentiation
InactiveUS20100088526A1More powerReduce in quantityDigital data processing detailsUnauthorized memory use protectionAlgorithmModular exponentiation
To calculate the equation y=xe mod n, integral to solving cryptographic and authentication problems, much computing power is required despite elegant algorithms that greatly reduce the number of calculations required. Operations involved in computing this equation include shifting bits, comparing values, subtracting, and adding. This invention provides an improvement over prior calculation methods by pinpointing places where computing cycles can be eliminated.
Owner:MCM PORTFOLIO LLC
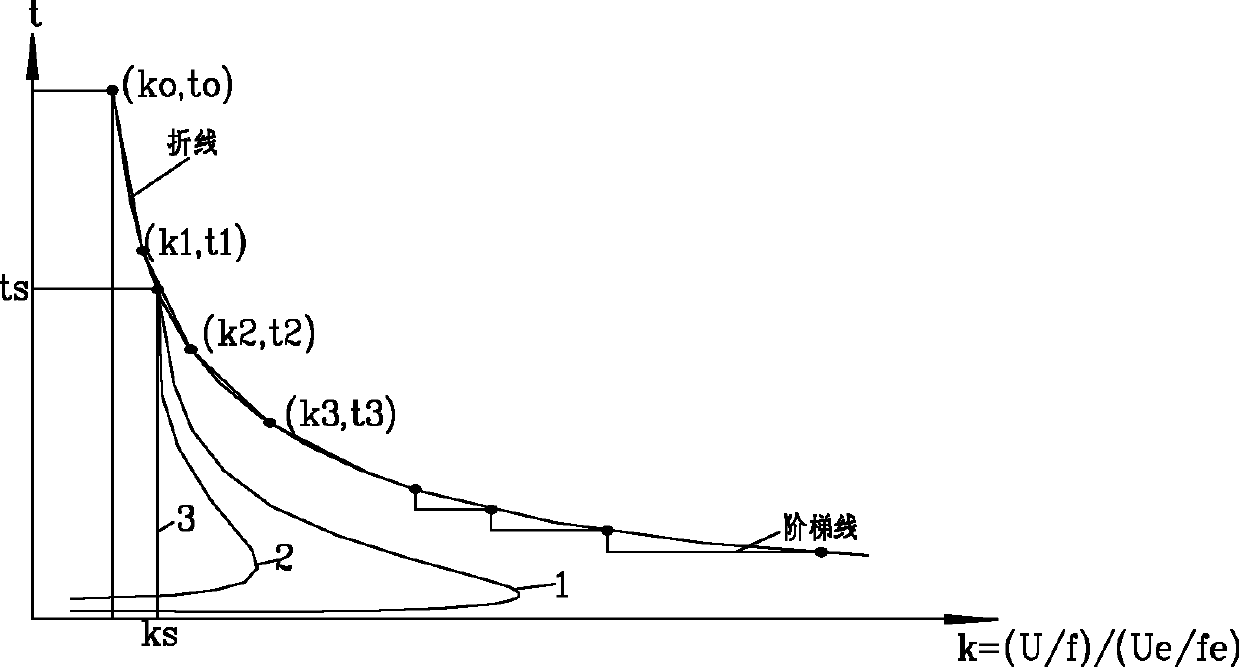
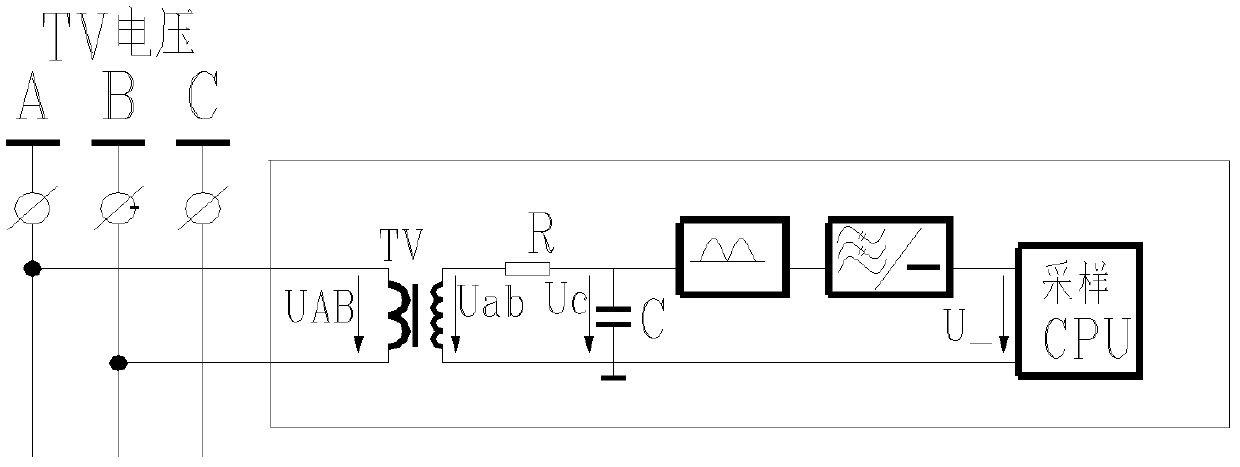
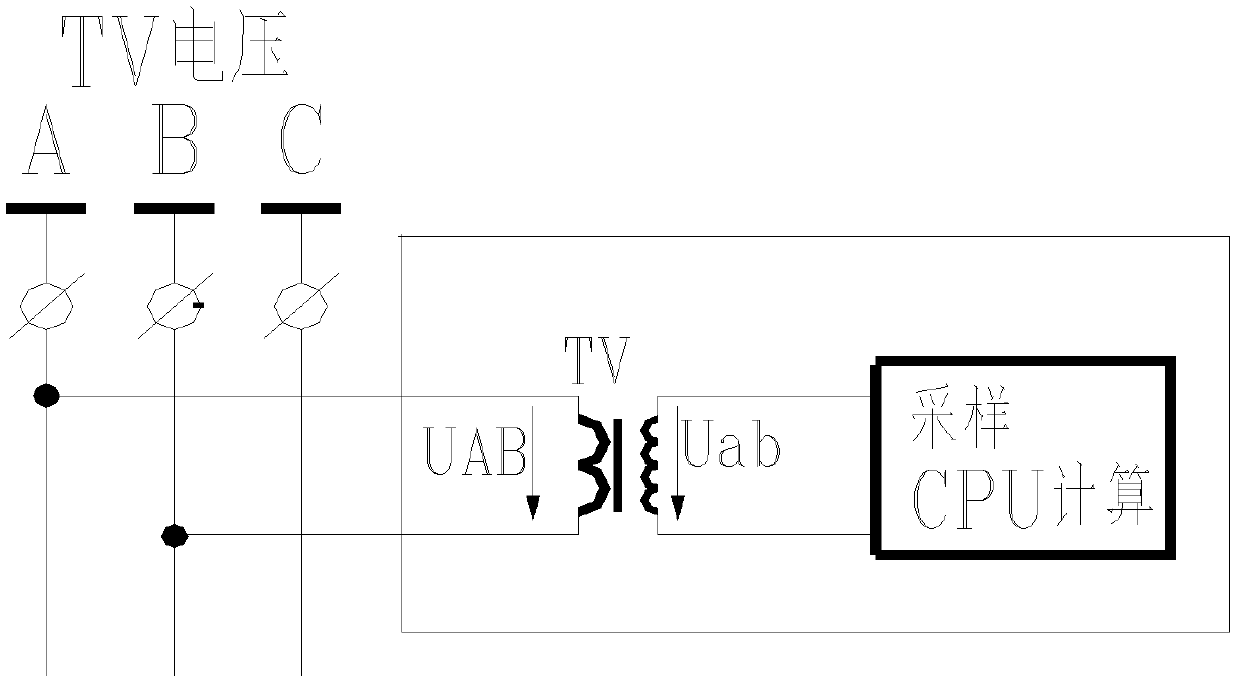
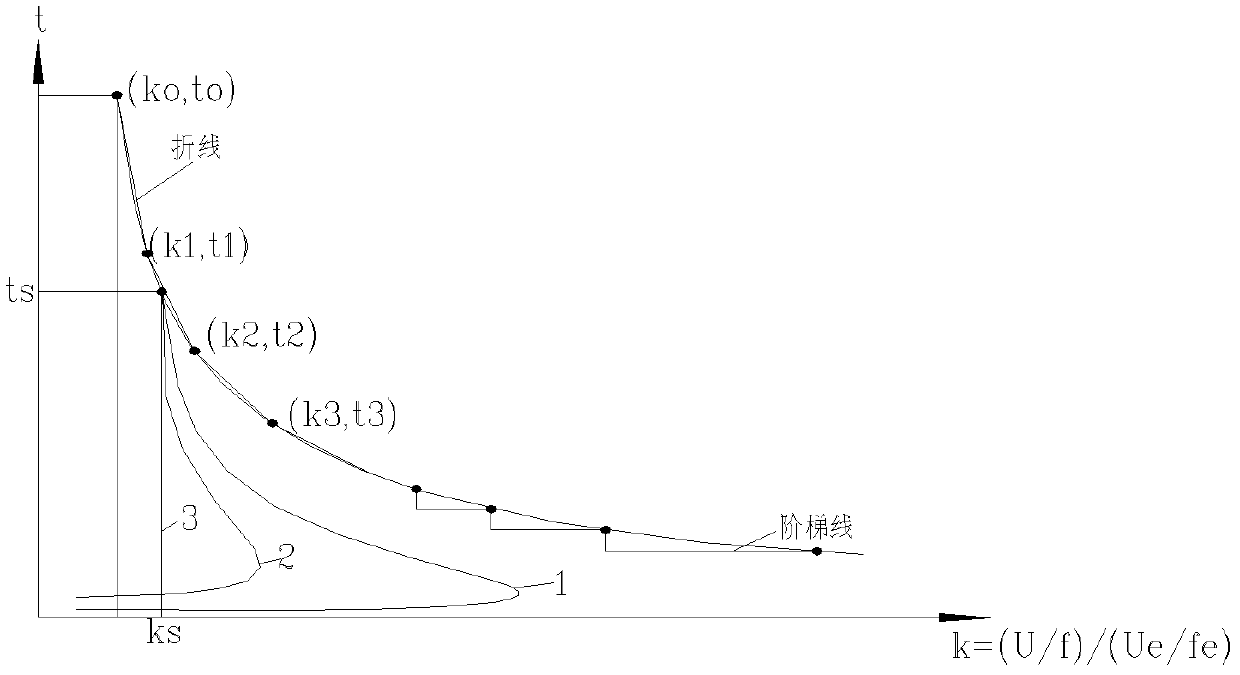
Half-wave integral accumulated-type inverse time-delay over-excitation protecting method
ActiveCN102354952AEasy to implementClear mathematical relationshipEmergency protective circuit arrangementsTime delaysTransformer
The invention discloses a half-wave integral accumulation-type inverse time-delay over-excitation protecting method, which is characterized by comprising the following steps that: 1) a voltage transformer is duly sampled to obtain a voltage instantaneous value; 2) harmonic voltage signal more than 150Hz is filtered through simple low-pass filtering, and then an over-excitation characteristic quantity U / f value is duly calculated through positive and negative half-wave integral superposition algorithm; 3) real over-excitation inverse time-delay curves are dispersed, and the curve fitting is realized by utilizing a multi-broken line or a staircase curve; 4) under the condition of the multi-broken line or the staircase curve, parameter transformation for reflecting an over-excitation dynamic variation process is adopted, so the multi-broken line or the staircase curve has an identical action boundary line under the condition of different U / f values; and 5) the transformation parameter values are superposed in real time according to the varied U / f values, and then the boundary off-limit judgment is executed so as to output protection action and transmit a signal. The half-wave integral accumulation-type inverse time-delay over-excitation protecting method has a small amount of calculation, and the algorithm is easy to realize.
Owner:GUODIAN NANJING AUTOMATION
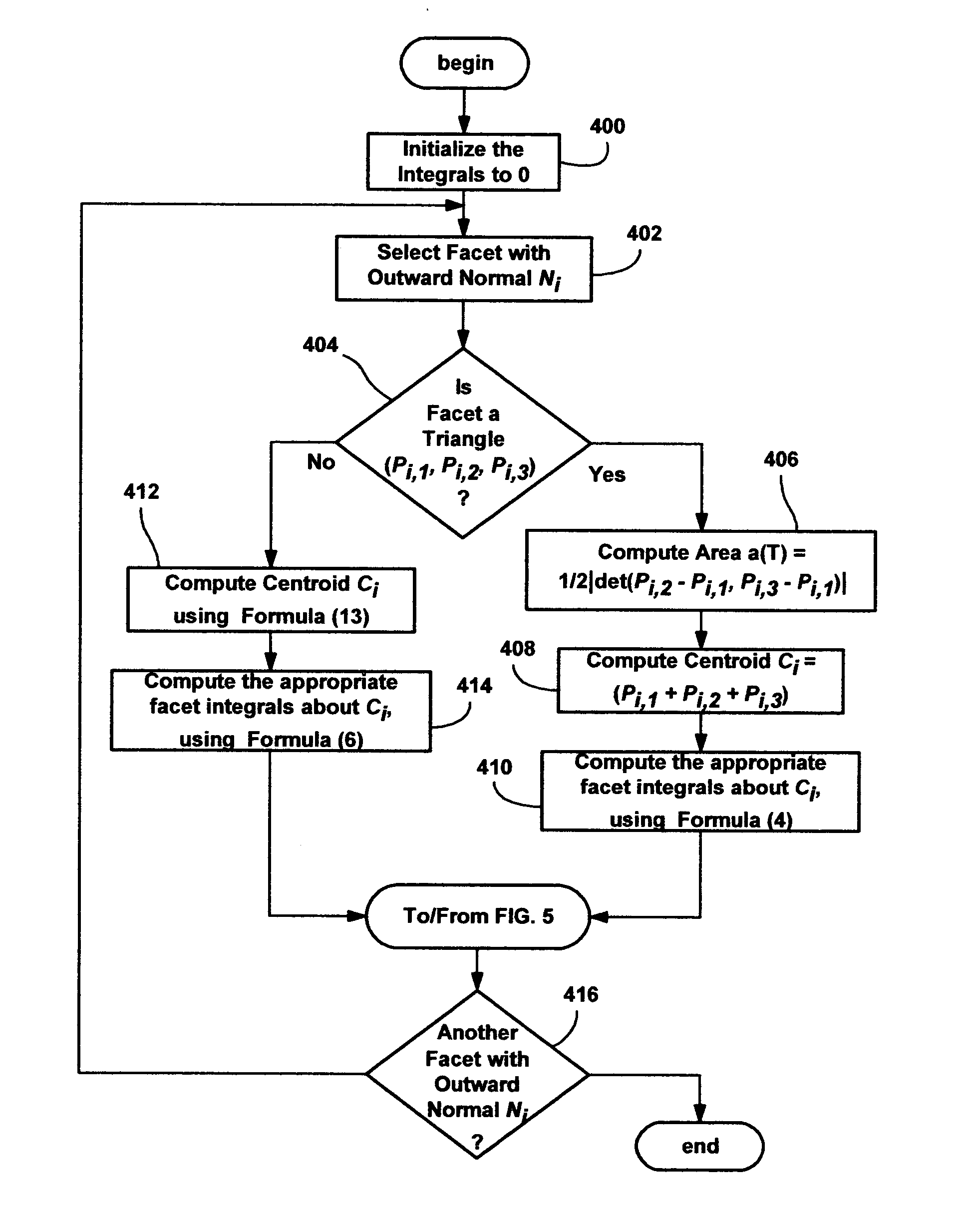
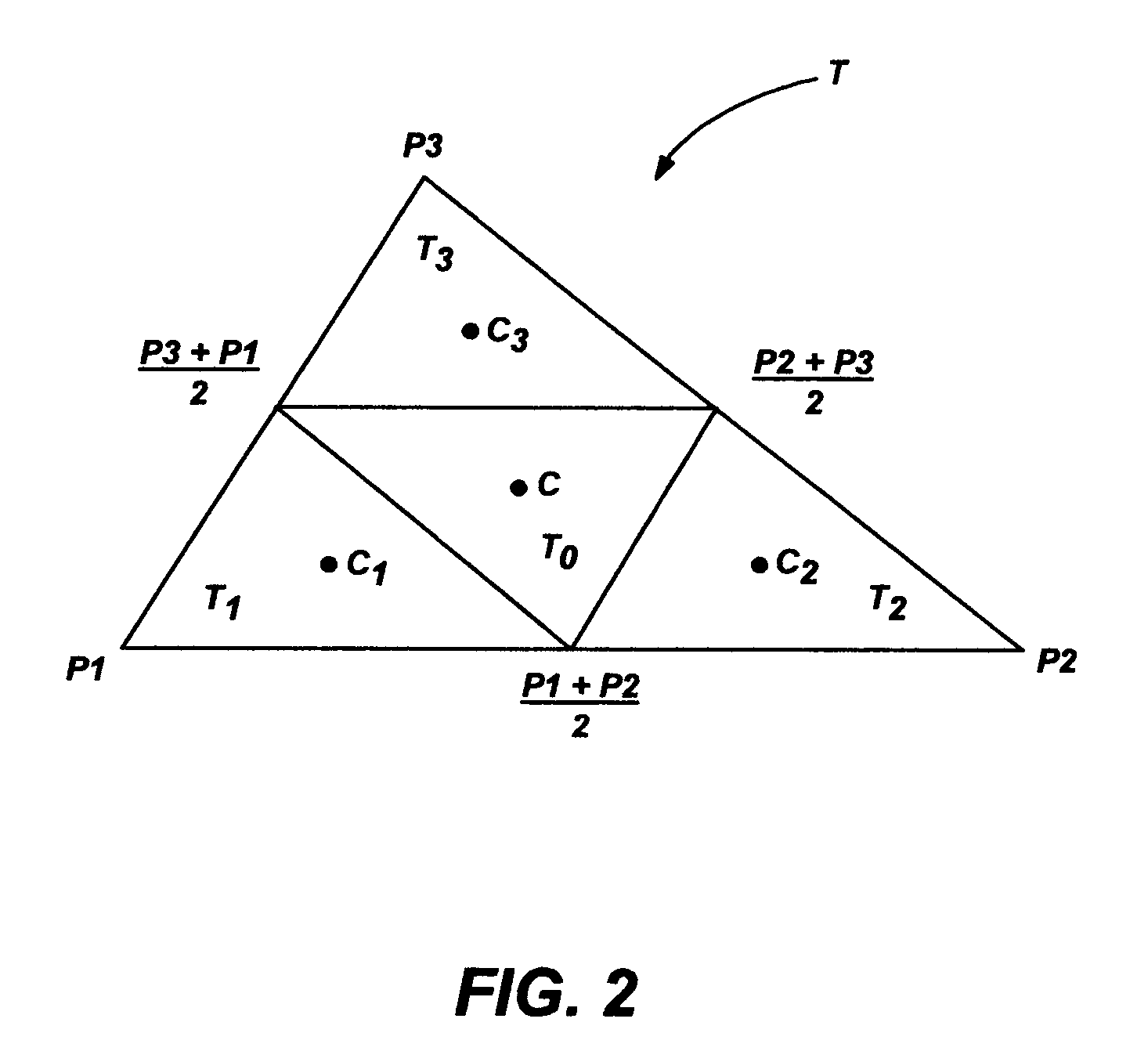
Method and system for computing the mass properties of polygons and polyhedra
InactiveUS20050021582A1Significant comprehensive benefitsPrevent integrationAnimation3D modellingGraphicsMoment of inertia
A method and system providing formulae that express integrals of quadratic homogeneous polynomials on polygons and polyhedra, such as entries of the moment of inertia tensor, in terms of vertex coordinates. The formulae for a triangle provide the mass properties without integration, and can be combined (using a signed sum) to determine the mass properties for any polygon. Likewise, the concept extends to a polyhedron, which may be built from a plurality of signed pyramids. An algorithm combines the formulae to determine the mass properties of a polyhedron. The formulae and algorithm may be used in a graphics processing environment.
Owner:MICROSOFT TECH LICENSING LLC
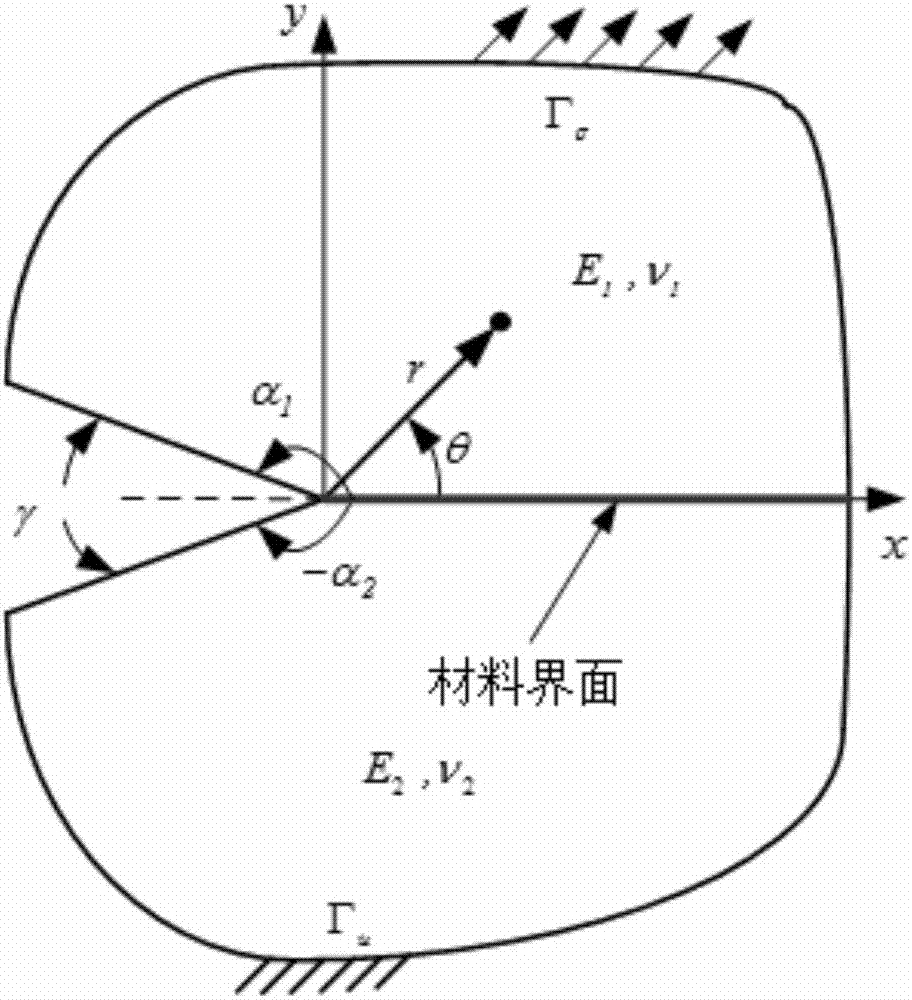
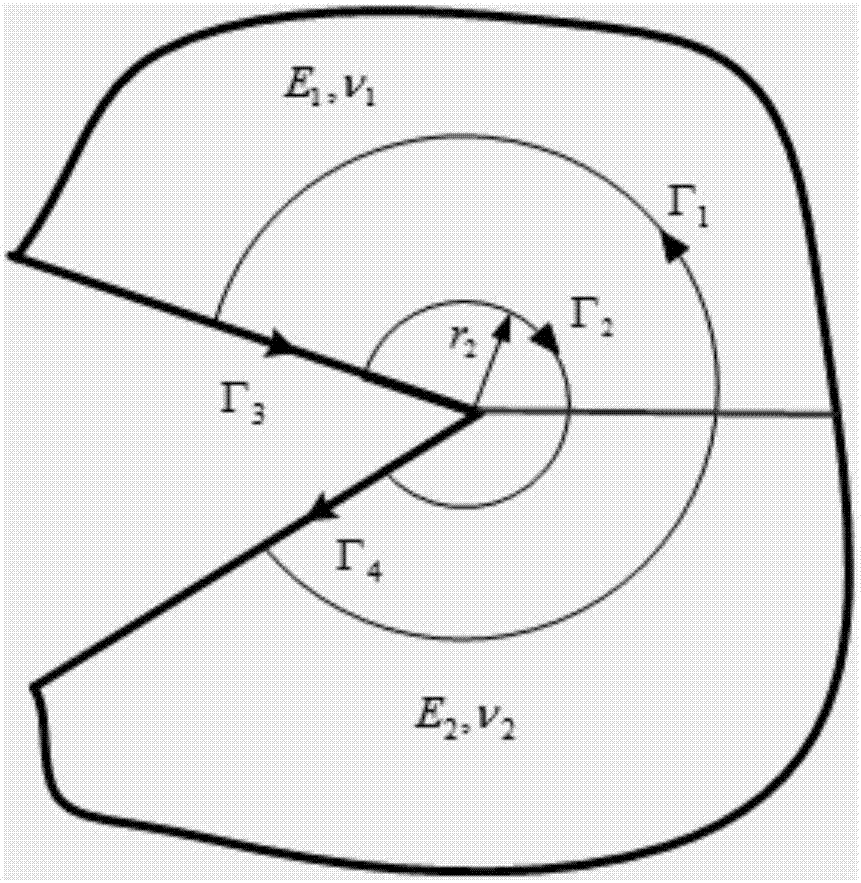
Bi-material V-shaped incision stress intensity factor calculation method
InactiveCN107958126AHigh precisionDesign optimisation/simulationSpecial data processing applicationsMedicineUltimate tensile strength
The invention discloses a bi-material V-shaped incision stress intensity factor calculation method. According to a characteristic equation of a bi-material V-shaped incision, a Muller method is adopted to calculate a characteristic value; according to the type of the characteristic value, a displacement expression of the bi-material V-shaped incision is obtained; an extended finite element displacement mode and a control equation of the bi-material V-shaped incision are built; the control equation is solved, and finally, through conservative integration, a stress intensity factor is calculated. According to the method, during finite element mesh dividing, the incision boundary and the material interface do not need to be taken into consideration, so that the efficiency of mesh generation is improved; meanwhile, stress intensity factor solving has nothing to do with a selected integration path so that good precision can be obtained.
Owner:HOHAI UNIV
Hierarchical tomographic reconstruction
The present disclosure relates to the use of a hierarchical tomographic reconstruction approach that employs data representations in intermediate steps are between a full line integral and a voxel (e.g., an intermediate line integral). Each of the steps is progressively more local in nature and therefore has computational advantages and is also amenable to a deep learning solution using trained neural networks. The proposed hierarchical structure provides a mechanism to divide a large-scale inverse problem into a series of smaller-scale problems.
Owner:GENERAL ELECTRIC CO
Double-layer integral using a static green's function and rectangular basis
InactiveUS20090144685A1Easy to useDesign optimisation/simulationSpecial data processing applicationsEmbedded systemGreen's function
Owner:IBM CORP
Fractal dimension calculating method based on density peak clustering
InactiveCN108921211AObjective and accurate automatic identificationExtensive spatial and temporal distribution characteristicsCharacter and pattern recognitionAlgorithmDensity based
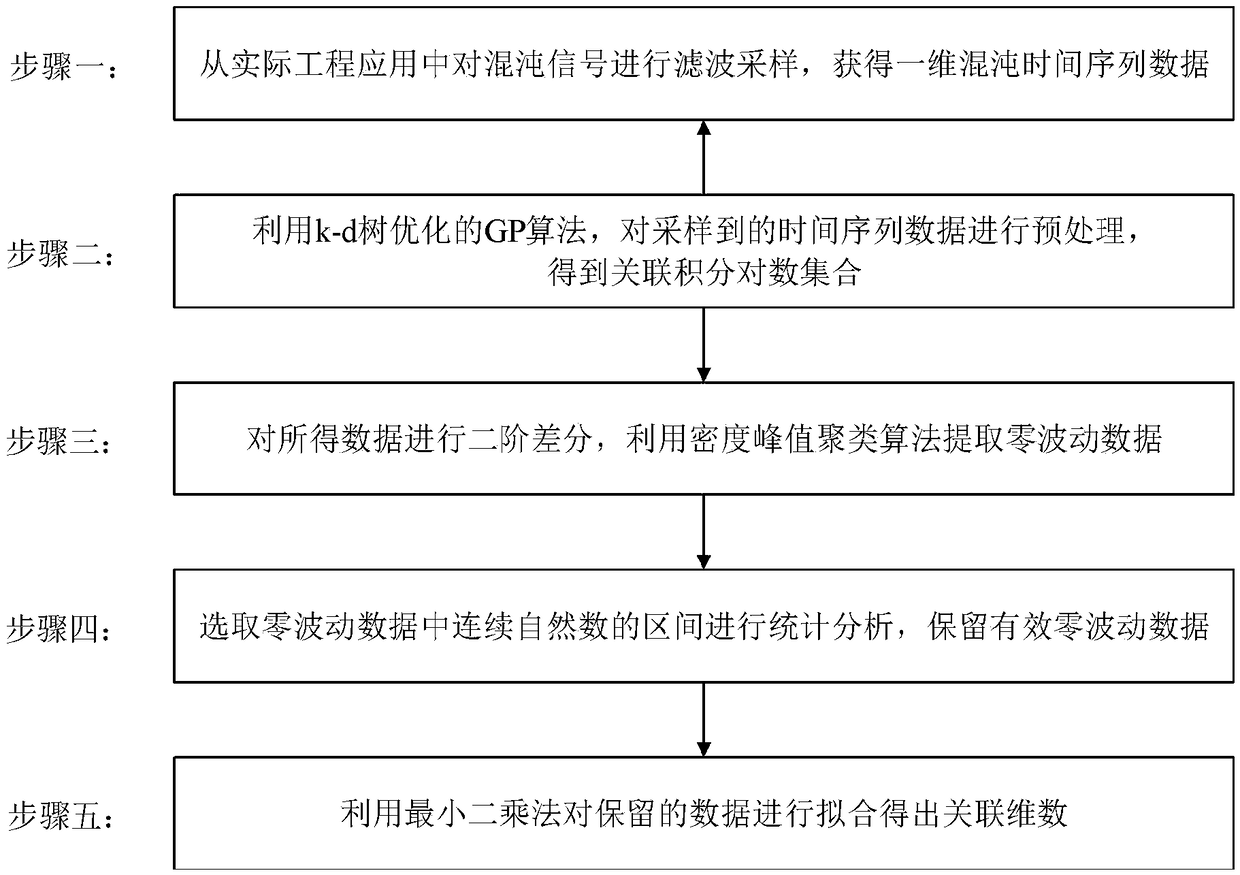
The invention relates to a fractal dimension calculating method based on a density peak clustering algorithm, and belongs to the field of signal processing. The fractal dimension calculating method comprises the following steps that S1, one-dimensional chaotic time series signals are obtained from practical engineering; S2, sampled time series data are subjected to pre-treatment to obtain an associative integral logarithmic set by using a k-d tree optimized GP algorithm; S3, second order difference is applied to obtained data, and zero fluctuation data are extracted by using the density peak clustering algorithm; S4, the interval of continuous natural numbers in the zero fluctuation data is selected to conduct statistical analysis, and effective zero fluctuation data are maintained; and S5, the reserved data are fitted by using the least square method, and the correlation dimension is calculated. A scale-free interval can be automatically recognized objectively and accurately, calculation results are more precise, the procedure is simple, achievement is easy, and great significance to nonlinear application is achieved.
Owner:CHONGQING NORMAL UNIVERSITY
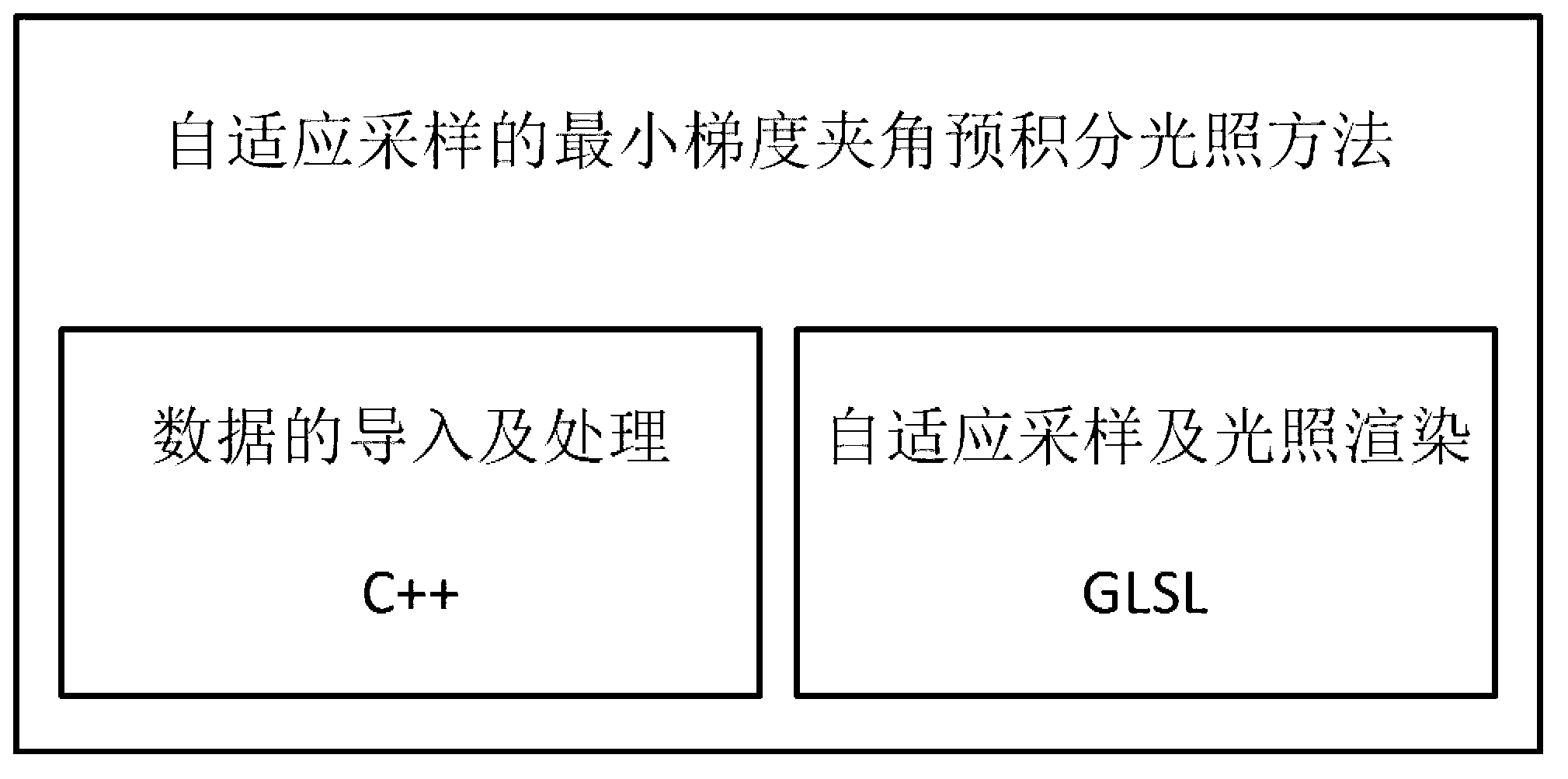
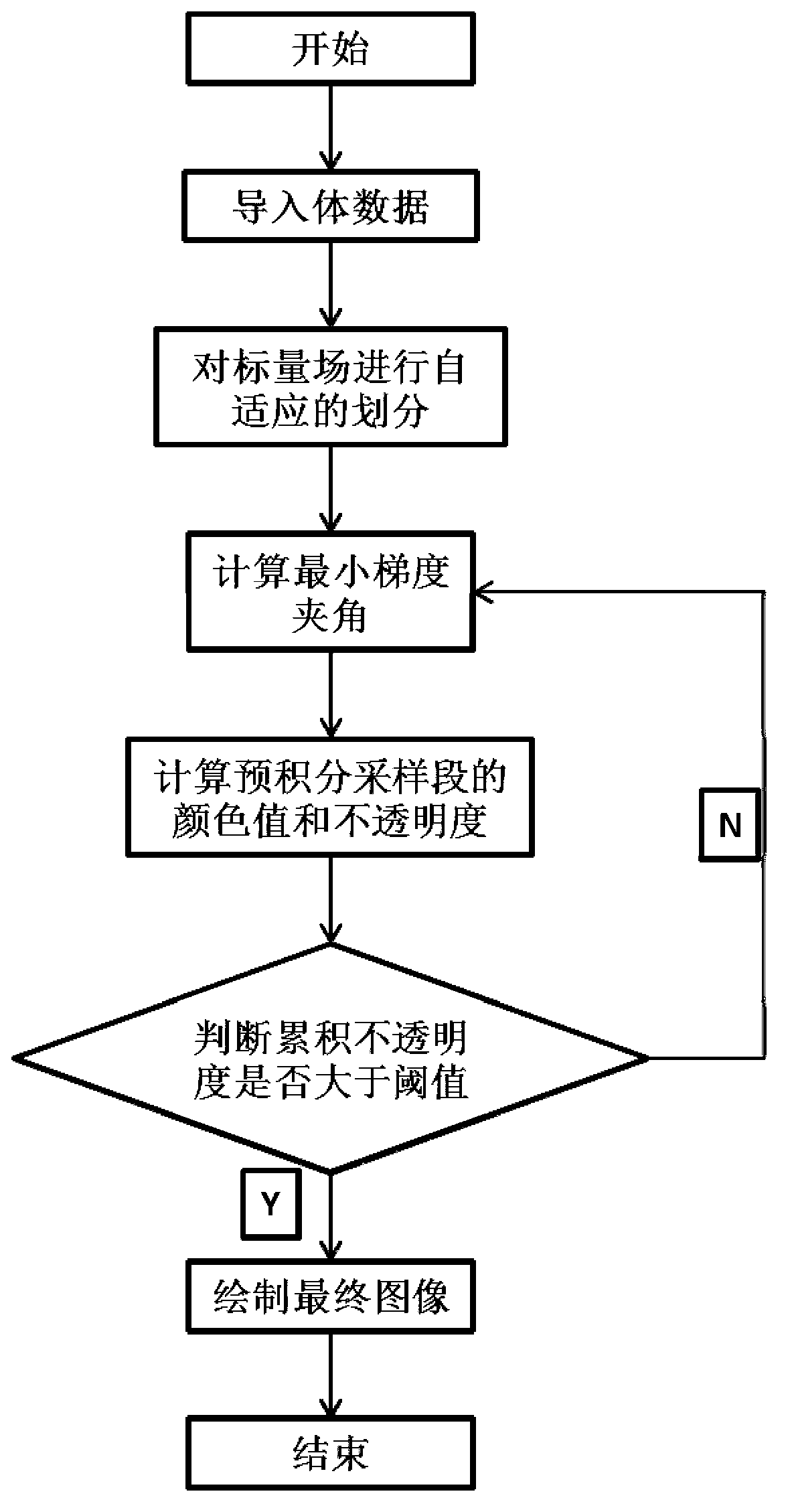
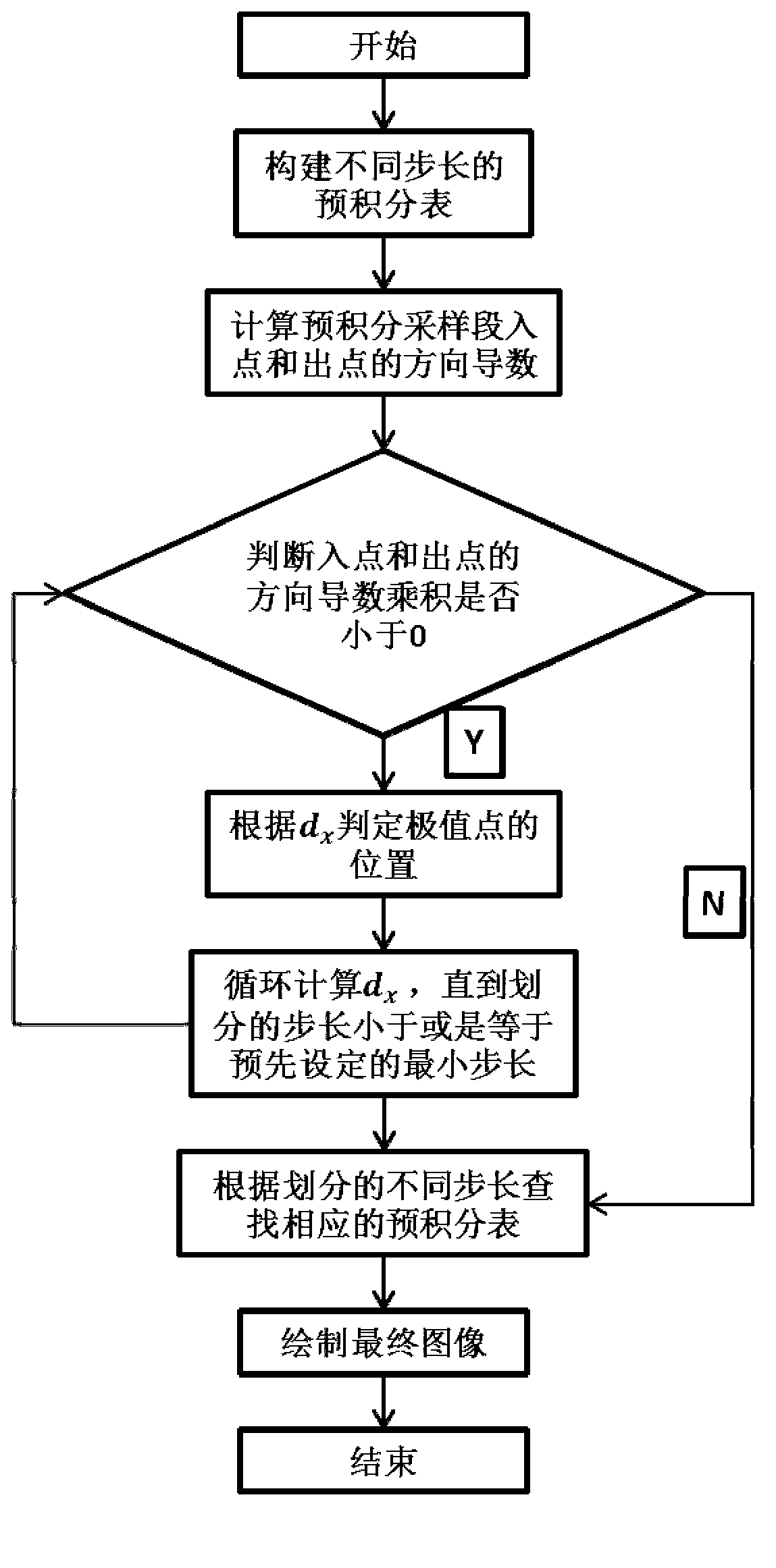
Minimum gradient included angle pre-integration illumination method of self-adaptive sampling
ActiveCN103295259AImprove lighting effectsQuality improvement3D-image renderingScalar fieldScalar Value
Discloses is a minimum gradient included angle pre-integration illumination method of self-adaptive sampling. The method includes that 1), medical volume data are imported; 2), multiple pre-integration lists with different step lengths are created, the number of the lists can be determined according to accuracy requirements of actual application, in the process of sampling, self-adaptive sampling is performed according to variation trend of a scalar field, small sampling step lengths can be adopted when extreme values are encountered in areas where scalar values vary dramatically; sampling step lengths can be correspondingly increased in areas where scalar values gently vary relatively; 3), gradients in pre-integration segments are reconstructed by means of interpolation reconstruction, the gradient, having the minimum included angle with the illumination direction, in pre-integration sampling segments is calculated, and the gradient is applied to pre-integration illumination rendering, so that illumination effect of local details is enhanced; 4), corresponding color values and opacity are acquired by searching the pre-integration lists with the different step lengths according to the pre-integration segments acquired by a self-adaptive sampling strategy, and volume rendering integration is performed.
Owner:ZHEJIANG UNIV OF TECH
A novel satellite signal FFT parallel-acquisition algorithm
InactiveCN106772468AImprove performanceSmall amount of calculationSatellite radio beaconingIntermediate frequencyOperation point
The invention relates to a novel satellite signal FFT parallel-acquisition algorithm widely applied to different satellite receivers. According to the invention, firstly, it is assumed that there is no bit flip; digital IF signals and local recurrent signals are subjected to cyclic correlation operation to get the related results; in the operation process, the FFT operation is divided into two parts of a sum to reduce the FFT operation points and calculated amount; and secondly, it is assumed that there is a bit flip; the digital IF signals and local recurrent signals are subjected to even-odd partitioning and correlation operation to obtain related result; meanwhile, in the operation process, the FFT operation is subjected to segmentation; and finally, the related results obtained at two times are compared, and the maximum is the maximum peak acquired. The novel parallel-acquisition algorithm designed by the invention can effectively overcome the problem of bit flip and prolong the coherence integration time. Compared with traditional acquisition algorithms, the calculated amount of the proposed novel acquisition algorithm is reduced. The whole process is relatively high in processing efficiency and relatively good in algorithm performance.
Owner:TAIYUAN UNIV OF TECH
Euler angle Hartley approximate output method based on angular speed
InactiveCN102495828AGuaranteed output accuracyGuaranteed time update iteration calculation accuracyComplex mathematical operationsLinear approximationHartley function
The invention discloses an Euler angle Hartley approximate output method based on angular speed, which is used for solving the technical problem of low Euler angle output precision of maneuver of the conventional aircraft. According to the technical scheme, the method comprises the following steps of: introducing multiple parameters and performing approximate description of the angular speeds of rolling, pitching and yawing (p, q and r) by using a polynomial of the Hartley function; determining the order of polynomial description of the angular speeds of rolling, pitching and yawing (p, q and r) according to the requirement on the engineering precision; and sequentially solving a pitching angle, a rolling angle and a yawing angle and directly performing high-order approximation integral on the expression of an Euler angle so that the Euler angle is solved in a super-linear approximation way, the precision of time update iterative computation for determining the Euler angle is ensured and the accuracy of the output flight attitude of inertia equipment is improved.
Owner:NORTHWESTERN POLYTECHNICAL UNIV
Angular velocity-based Euler angle Fourier approximate output method
InactiveCN102519457AGuaranteed output accuracyNavigational calculation instrumentsNavigation by speed/acceleration measurementsAngular velocityIntegral of secant cubed
The invention discloses an angular velocity-based Euler angle Fourier approximate output method, which is used for solving the technical problem of low Euler angle output accuracy when the conventional aircraft performs maneuver flight. According to the technical scheme, a plurality of parameters are introduced, Fourier series is adopted for approximate description of the rolling, pitch and yaw rates p, q and r, the rolling, pitch and yaw rates p, q and r are solved in turn according to the order of the Fourier series description of the rolling, pitch and yaw rates p, q and r, and an expression formula of a Euler angle is directly subjected to high-order approximation integral, so that the solution of the Euler angle approximates according to superlinearity, the iterative calculation accuracy of determining the time update of the Euler angle is ensured, and the accuracy of outputting a flight attitude by inertial equipment is improved.
Owner:NORTHWESTERN POLYTECHNICAL UNIV
Angular velocity based Euler angle Laguerre exponent approximate output method
InactiveCN102519468AGuaranteed output accuracyInstruments for comonautical navigationAngular velocityUltra-linear
The invention discloses an angular velocity based Euler angle Laguerre exponent approximate output method, which is used for solving the technical problems that the Euler angle output precision is poor when the traditional aircraft maneuvers. The technical scheme is as follows: roll, pitch, and yaw rates p, q, r expand according to Laguerre orthogonal polynomials by introducing a plurality of parameters; by sequentially solving a pitch angle, a roll angle and a yaw angle, the high-order approximation integral of the expression of an Euler angle is directly conducted, so that the solution of the Euler angle is in accordance with ultra-linear approximation, and the determination of time updating iterative calculation accuracy of the Euler angle is ensured, and thus the accuracy of the output of a flight attitude of inertial equipment is improved.
Owner:NORTHWESTERN POLYTECHNICAL UNIV
A formal verification method of Laplace transform based on Coq
The invention discloses a formal verification method of Laplace transform based on Coq, which formally defines the Laplace transform in the theorem prover Coq and verifies the main properties of the Laplace transform. As that theorem prove Coq is precise and reliable, the method solves the disadvantage that the traditional method cannot accurately verify the Laplace transform. the method mainly includes the following steps: (1) The definition of Laplace transform is formalized by using the theories of differential, integral, limit, complex number and complex variable function in theorem proverCoq; (2) the formalization of the existence theorem of Laplace transform: the formalization of the existence theorem of Laplace transform; (3) The formal proof of the basic properties of Laplace transform: The linear properties, frequency shift properties, differential properties and integral properties of Laplace transform are formally proved in Coq theorem prover.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Hartley Approximate Output Method of Euler Angle Based on Angular Velocity
InactiveCN102495828BGuaranteed output accuracyGuaranteed time update iteration calculation accuracyComplex mathematical operationsAngular velocityLinear approximation
The invention discloses an Euler angle Hartley approximate output method based on angular speed, which is used for solving the technical problem of low Euler angle output precision of maneuver of the conventional aircraft. According to the technical scheme, the method comprises the following steps of: introducing multiple parameters and performing approximate description of the angular speeds of rolling, pitching and yawing (p, q and r) by using a polynomial of the Hartley function; determining the order of polynomial description of the angular speeds of rolling, pitching and yawing (p, q and r) according to the requirement on the engineering precision; and sequentially solving a pitching angle, a rolling angle and a yawing angle and directly performing high-order approximation integral on the expression of an Euler angle so that the Euler angle is solved in a super-linear approximation way, the precision of time update iterative computation for determining the Euler angle is ensured and the accuracy of the output flight attitude of inertia equipment is improved.
Owner:NORTHWESTERN POLYTECHNICAL UNIV
Half-wave integral accumulated-type inverse time-delay over-excitation protecting method
ActiveCN102354952BEasy to implementClear mathematical relationshipEmergency protective circuit arrangementsTransformerTime delays
Owner:GUODIAN NANJING AUTOMATION
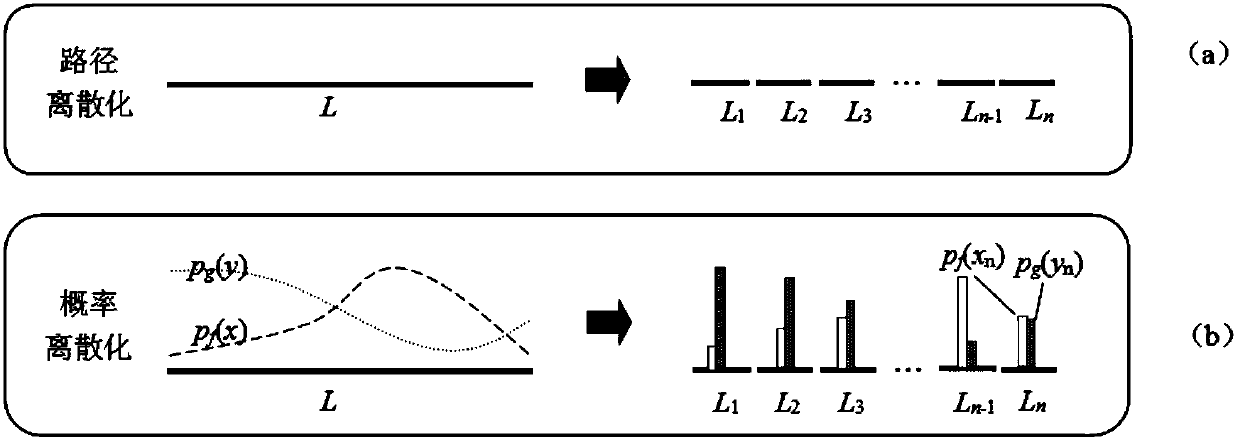
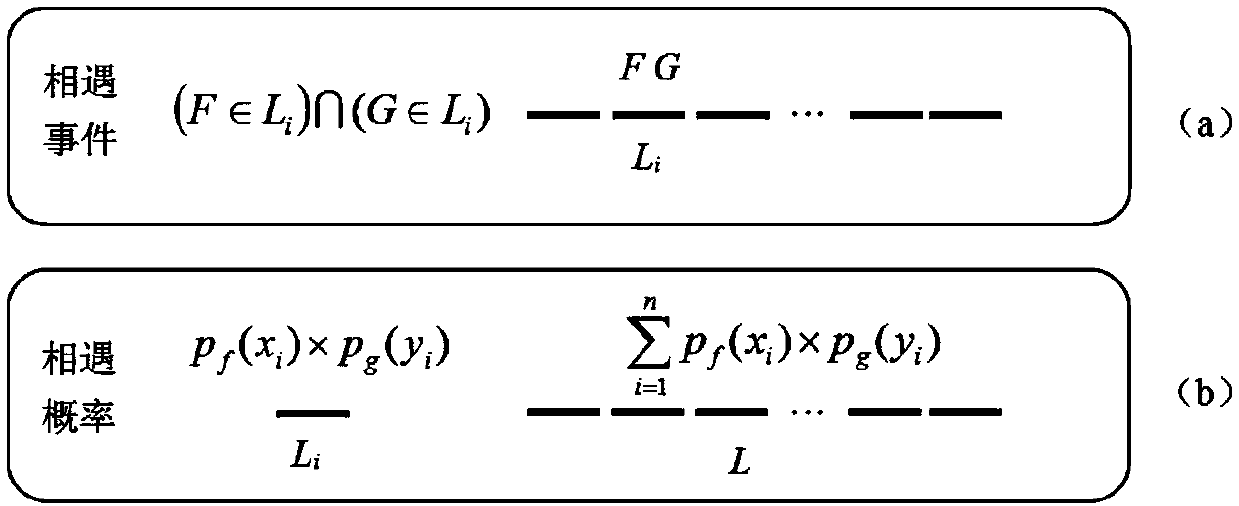
Discrete calculating method for meeting probability on continuous path
The invention discloses a discretization calculation method of encounter probability on a continuous path, which is used to calculate the encounter probability of a searcher F and a lost person G, comprising the following steps: Step 1: Preparatory work: discretization of the path, determining the length l of the path and the number of discrete units n; step 2: discretize the continuous probability; step 3: analyze the encounter event Emeet according to the maximum encounter distance; step 4: use the formula to calculate the encounter probability pmeet between the searcher F and the lost person G. The invention discretizes the complex continuous probability distribution of the moving object into a single probability value, transforms the integration problem of the encounter probability into the summation problem of the discrete probability, and is applicable to the calculation of the encounter probability in the continuous path.
Owner:WUHAN UNIV OF TECH
Electromagnetic transient rapid simulation method for controllable series compensation device
ActiveCN110059346AQuick solveCalculation is efficient and time-savingFlexible AC transmissionSpecial data processing applicationsEngineeringSystem of differential equations
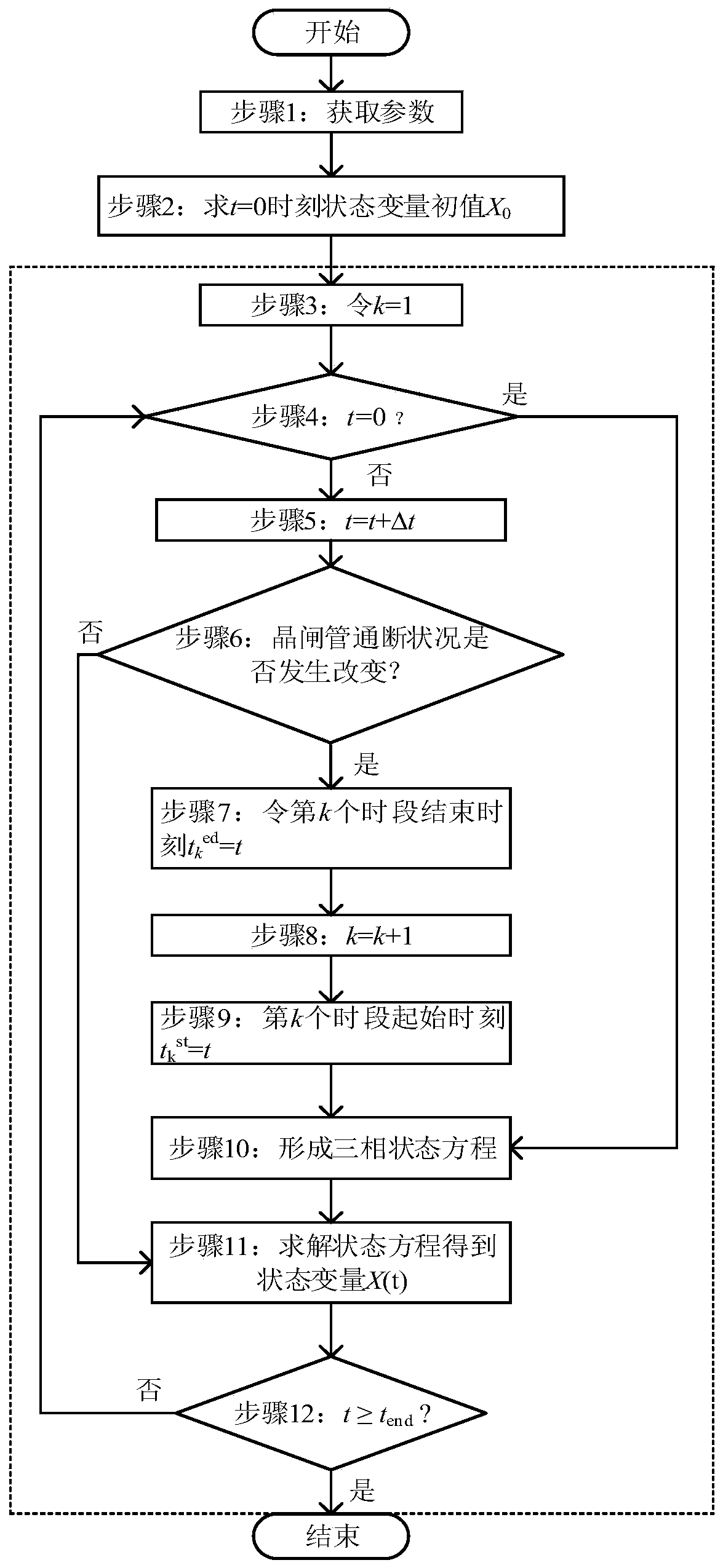
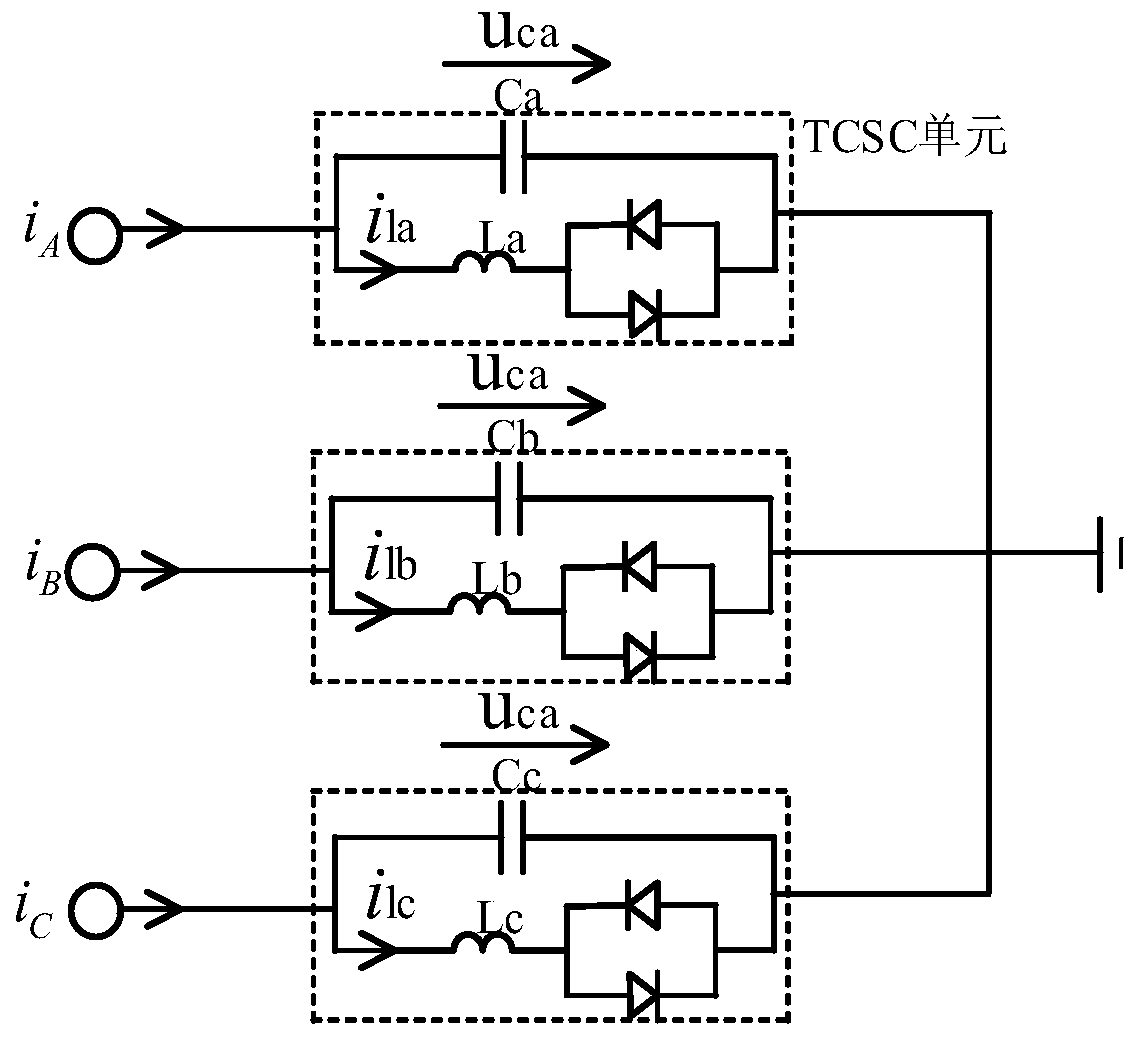
The invention discloses an electromagnetic transient rapid simulation method of a controllable series compensation device. The method comprises the following steps: step 1, obtaining parameters; obtaining basic data including inductors La, Lb and Lc of a three-phase TCSC branch circuit, capacitors Ca, Cb and Cc of the three-phase TCSC branch circuit, expressions of three-phase current sources iA,iB and iC and an initial trigger angle alpha 0. According to the method, sine auxiliary variables are introduced, a state equation of the TCSC is converted into a homogeneous linear differential equation set from a non-homogeneous linear differential equation set, the state equations are unified in form under all working conditions, and the homogeneous linear differential equation set can be quickly solved through a matrix index integration method; compared with the fact that a system model required to be solved changes in each time step in traditional electromagnetic transient calculation, the method has the advantages that the system model required to be solved can be changed only when the on / off states of the thyristors are changed, so that the calculation is more efficient and time-saving.
Owner:GUANGDONG UNIV OF TECH
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com