Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

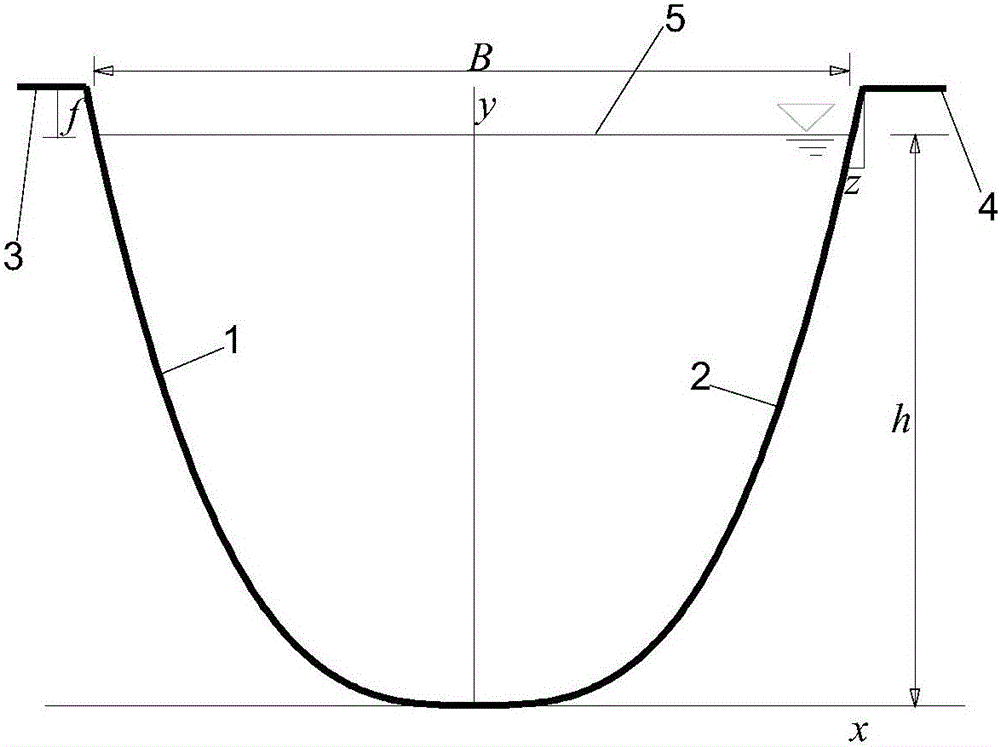
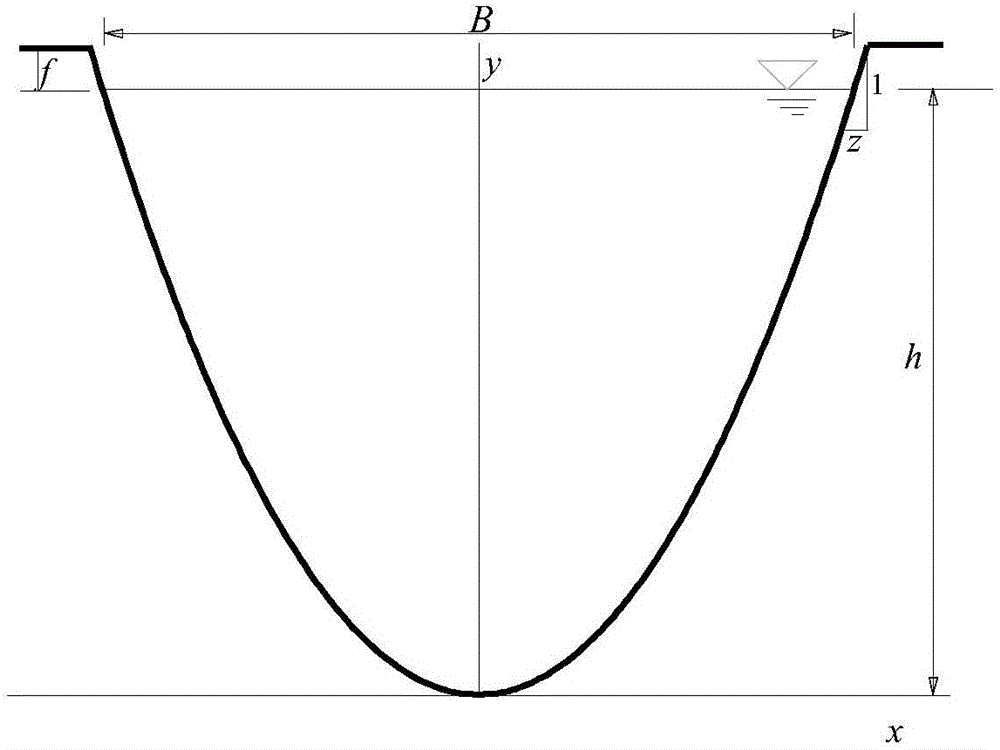
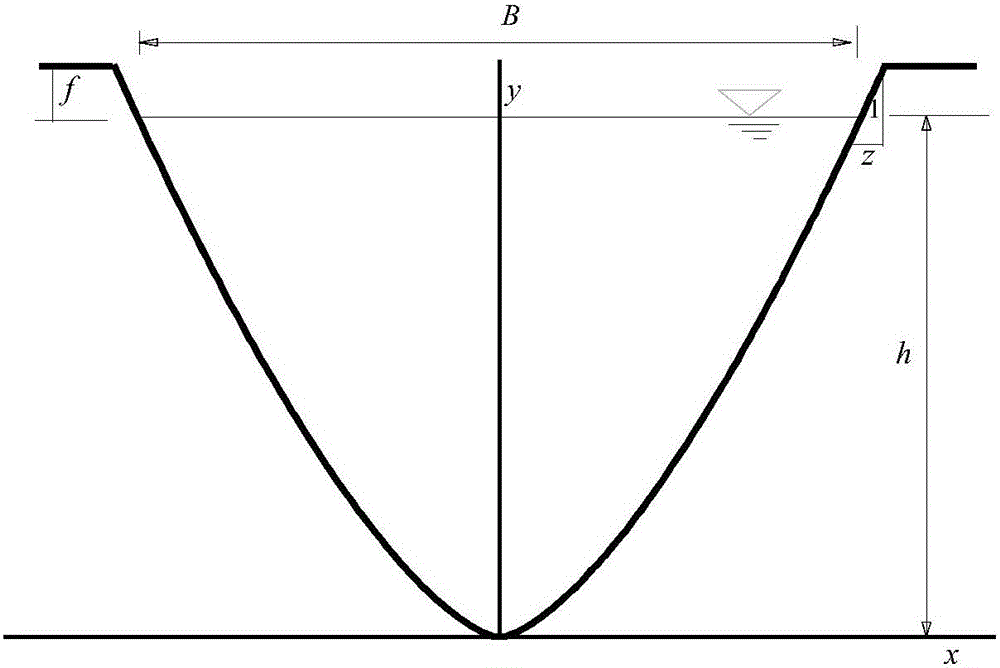
Waterpower optimal section of cubic parabola shaped water conveying open channel, and solving method for cubic parabola shaped waterpower optimal section

A parabola-shaped, optimal cross-section technology, applied in the direction of instruments, data processing applications, prediction, etc., can solve the problems of complicated calculation of cross-section wetted circumference and inconvenient engineering practice

Active Publication Date: 2016-09-07
UNIV OF JINAN
View PDF3 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0008] Aiming at the problem that the calculation of the wetted perimeter of the section of the existing water delivery channel is complicated and not convenient for engineering practice, an explicit expression for calculating the wetted perimeter is proposed, which is not only simple to calculate, but also has good accuracy

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Waterpower optimal section of cubic parabola shaped water conveying open channel, and solving method for cubic parabola shaped waterpower optimal section
  • Waterpower optimal section of cubic parabola shaped water conveying open channel, and solving method for cubic parabola shaped waterpower optimal section
  • Waterpower optimal section of cubic parabola shaped water conveying open channel, and solving method for cubic parabola shaped waterpower optimal section

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0241] Example 1 (Approximate Solution of Wet Perimeter)

[0242] Two cubic parabolic channel sections, shape coefficient a = 0.5, water depth h = 1.5m, calculate the wetted circumference.

[0243] First use formula (3) to get

[0244] Using the method of numerical integration, the theoretical value of the wet perimeter is obtained Integral method is generally obtained with the help of computer programs, which is not suitable for engineering practice. Using the approximate formula provided by the present invention The error is only 0.0057m. When h = 1.0 ~ 2.5m, use the approximate method and the integral method to calculate the wet area respectively, and the results are shown in Table 3.

[0245] Table 3 Comparison table of wetted area calculated by approximation method and integral method

[0246] Water depth h(m)

[0247] From the calculation results, this approximation algorithm has high precision.

example 2

[0248] Example 2 (known flow, design channel section)

[0249] There is a channel, known Q=10m 3 / s,So =1 / 15000, n=0.014s / m 1 / 3 . Now it is necessary to design a channel, which requires the minimum flow area and wetted area under a certain flow capacity, or the maximum flow capacity under a certain area.

[0250] According to cubic parabolic section design: Substituting the known data into formula (31), formula (32) ~ formula (34) and formula (25), it can be obtained that h = 2.91m, B = 6.14m, A = 13.39m 2 , P=9.25m, a=0.100.

[0251] According to quadratic parabola design: substituting the known data into formula (37), formula (35) and formula (38) ~ formula (40), it can be obtained that h=3.13m, a=0.302, B=6.45m, A= 13.49m 2 , P=9.41m.

[0252] Design according to other cross-sectional shapes: the same method can be used to calculate the design dimensions of semi-cubic parabola, trapezoidal cross-section and catenary cross-section, as shown in Table 4.

[0253] It can...

example 3

[0257] Example 3 (comparison of flow capacity and construction cost)

[0258] A water delivery channel with a total length of 100Km. Q=12m 3 / s,n=0.014s / m 1 / 3 ,S o =1 / 20000, f=0.5m. Unit canal length, lining cost C l = 50 yuan / m 2 , earthwork excavation cost C e 30 yuan / m 2 , land acquisition fee C a = 15 yuan / m. The local hydrogeological conditions are good, and the slope coefficient is not limited. Now it is necessary to design a hydraulic optimum section and calculate the construction cost.

[0259] Substituting the known data into Table 1, the dimensions of different shapes (cubic parabola, quadratic parabola, semi-cubic parabola, catenary shape, trapezoid) can be obtained, and the results are listed in Table 5. From the comparison results, it can be obtained that the cubic parabolic channel section has the smallest water depth, water surface width, water passing area and wetted area, or in other words, under the same conditions, it has the largest flow capacity...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a cubic parabola shaped waterpower optimal section of a water conveying open channel, and a solving method for the cubic parabola shaped waterpower optimal section. The waterpower optimal section employs a cubic parabola shaped section, and is expressed as y=ax<3>, wherein the optimal width to depth ratio is B / h=2.1139, the shape coefficient a=0.8469h<-2>, and the side slope coefficient of a water surface is z=1 / 6* B / h=0.3523. The solving method comprises the steps: firstly designing the shape of the waterpower section of the water conveying open channel as the cubic parabola shaped waterpower section, and solving the characteristics of the waterpower section; secondly building a solving model for the waterpower optimal section; thirdly solving a differential equation of the waterpower optimal section through employing the Lagrangian multiplier method; fourthly enabling a wetted perimeter to be expressed as an expression of a complete elliptic integral function in a complex field range; and finally converting an optimal section problem into an equation with one unknown quantity in the complex field range, and obtaining the width to depth ratio of the waterpower optimal section. The waterpower optimal section is larger in discharge capacity under the condition of equal area or wetted perimeter, facilitates the improvement of the water conveying efficiency, and is low in construction cost.

Description

technical field [0001] The invention relates to a water delivery channel, in particular to a hydraulic optimum section of a cubic parabolic open water delivery channel and a solution method thereof, and belongs to the technical field of planning and design of water delivery channels in irrigation areas. Background technique [0002] Channel water delivery section is of great significance to channel water delivery. A good channel section can not only increase the water delivery capacity and reduce the water delivery cost, but also reduce the construction cost. The known parabolic channel section is quadratic parabolic (y=ax 2 ) (a is the shape factor, y is the ordinate, x is the abscissa), such as figure 2 shown. Some scholars have also studied the semi-cubic parabola (y=ax 3 / 2 ) section, such as image 3 shown. It should be noted that it is inaccurate for some domestic scholars to refer to the semi-cubic parabola section as a cubic parabola (such as: Yang Guoli, Wei We...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/04G06Q50/06
Inventor 韩延成
Owner UNIV OF JINAN
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com