Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

An Error Constrained Control Method for Unmanned Surface Vehicle Considering Input Saturation

A technology of error constraints and control methods, applied in two-dimensional position/channel control, adaptive control, general control system, etc., can solve the problem of low navigation control accuracy of surface unmanned boats

Active Publication Date: 2021-12-10
HARBIN ENG UNIV
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to solve the problem of low accuracy of navigation control of existing surface unmanned boats, and to propose an error-constrained control method for surface unmanned boats that considers input saturation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • An Error Constrained Control Method for Unmanned Surface Vehicle Considering Input Saturation
  • An Error Constrained Control Method for Unmanned Surface Vehicle Considering Input Saturation
  • An Error Constrained Control Method for Unmanned Surface Vehicle Considering Input Saturation

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

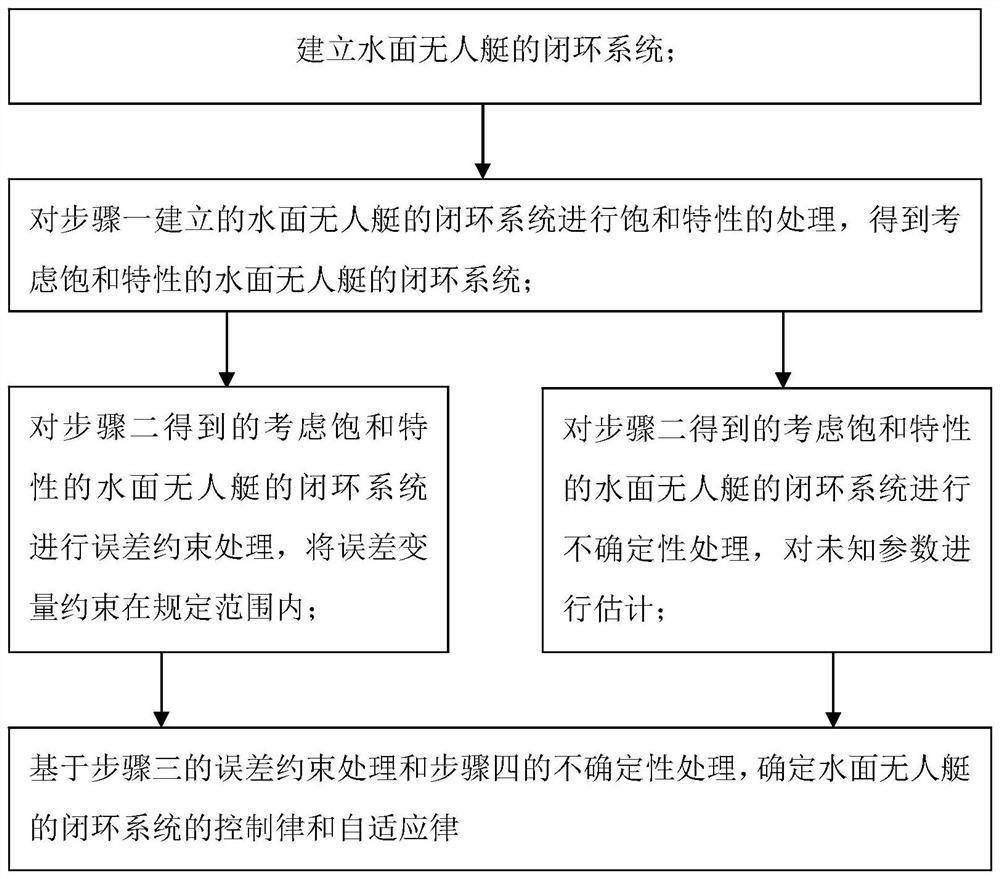
[0031] Specific implementation mode one: combine figure 1 Describe this embodiment, the specific process of an error-constrained control method for an unmanned surface vehicle considering input saturation in this embodiment is:

[0032] Ground coordinate system (O-XY): The coordinate origin O is located at the junction of the mooring line and the mooring terminal, and the plane where the XY axes are located is parallel to the ground.

[0033] Satellite coordinate system (o-xy): the origin o of the coordinates is located at the center of gravity of the surface unmanned boat, the x-axis points from the stern to the bow along the longitudinal axis, and the y-axis points to the port side.

[0034] Trajectory tracking control method: pre-set the sailing route of the surface unmanned boat, and control the surface unmanned boat to sail according to this trajectory.

[0035] Barrier Lyapunov function method in tan form: a state constraint control method based on the potential functi...

specific Embodiment approach 2

[0045] Specific embodiment two: the difference between this embodiment and specific embodiment one is that the closed-loop system of the surface unmanned boat is established in the step one; the specific process is:

[0046] Determine the symmetric positive definite inertia matrix M, the centripetal force and Coriolis force matrix C(ν), and the damping matrix D(ν);

[0047] According to the nature and hydrodynamic parameters of the target surface unmanned vehicle, the above M, C(ν), D(ν) can be determined;

[0048] Based on the symmetric positive definite inertia matrix M, the centripetal force and Coriolis force matrix C(ν), and the damping matrix D(ν), determine the non-singular transformation matrix J(η) of the surface unmanned vehicle from the satellite coordinate system to the ground coordinate system ;

[0049] And establish restoring force g (η) and unknown disturbance w according to the corresponding situation;

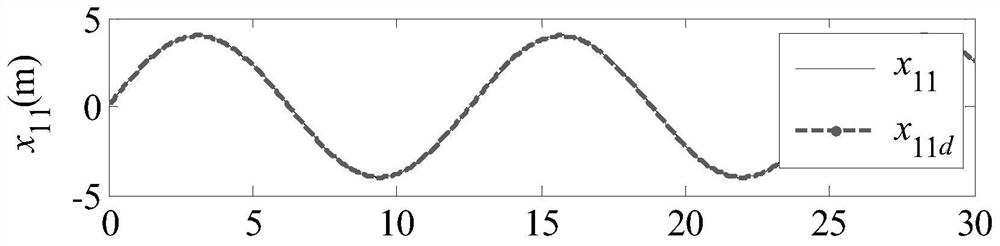
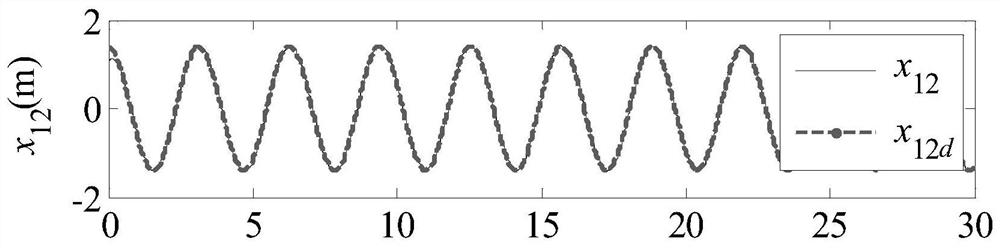
[0050] build the desired trajectory x 1d =[x 11d (t)...

specific Embodiment approach 3

[0063] Specific embodiment three: what this embodiment is different from specific embodiment one or two is that the inertial matrix M of described symmetry positive definite, centripetal force and Coriolis force matrix C (ν), and the expression of damping matrix D (ν) are as follows :

[0064]

[0065]

[0066]

[0067] Among them, m is the mass of the target surface unmanned vehicle, X du is the acceleration coefficient of the longitudinal force with respect to the movement along the x-axis of the body coordinate system, Y dv is the acceleration coefficient of the lateral force with respect to the movement along the y-axis of the body coordinate system, Y dr is the acceleration coefficient of the lateral force with respect to the z-axis rotation of the body coordinate system, x g is the longitudinal position of the center of gravity of the surface unmanned vehicle in the satellite coordinate system, N dr is the acceleration coefficient of the yaw moment with respe...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

An error-constrained control method for an unmanned water surface vehicle considering input saturation, and the invention relates to an error-constrained control method for an unmanned surface water vehicle. The purpose of the present invention is to solve the problem of low accuracy of the navigation control of the existing unmanned surface boat. The process is: 1. Establish the closed-loop system of the surface unmanned vehicle; 2. Obtain the closed-loop system of the surface unmanned vehicle considering the saturation characteristics; 3. Perform error constraint processing on the closed-loop system of the surface unmanned vehicle considering the saturation characteristics obtained in the second step , to constrain the error variable within the specified range; 4. To deal with the uncertainty of the closed-loop system of the surface unmanned vehicle considering the saturation characteristics obtained in 2, and estimate the unknown parameters; 5. Based on the error constraint processing of 3 and the Uncertainty treatment, determine the control law and adaptive law of the closed-loop system of the surface unmanned vehicle. The invention is used in the field of error-constrained control of the surface unmanned boat.

Description

technical field [0001] The invention relates to an error constraint control method for an unmanned water surface vehicle. Background technique [0002] At present, with the advancement of science and technology, the research on marine unmanned vehicles has also made great progress, such as surface unmanned boats, unmanned underwater vehicles, autonomous underwater vehicles, etc. have been put into practical applications. Among them, the surface unmanned vehicle, as an unmanned vehicle with high feasibility and wide range of uses, can perform various tasks such as monitoring of the marine environment and development of resources, so it has extremely high research value. At present, the commonly used control methods for surface unmanned vehicles include trajectory tracking control, path tracking control, formation control and so on. [0003] The trajectory tracking control method refers to setting the navigation route of the surface unmanned boat in advance, and controlling t...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04G05D1/02
CPCG05B13/042G05D1/0206
Inventor 孙延超秦洪德李骋鹏李晓佳陈辉吴哲远李凌宇
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com