Generation method based on Edwartz curve digital signature
A digital signature and curve technology, applied in the field of information security, can solve problems such as multiple storage spaces, inability to use, and security issues
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
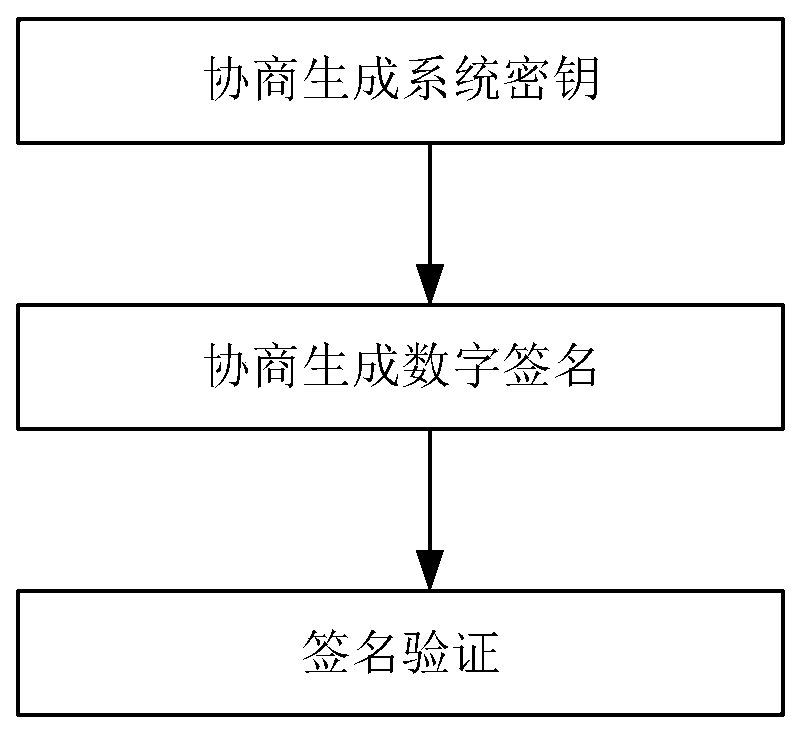
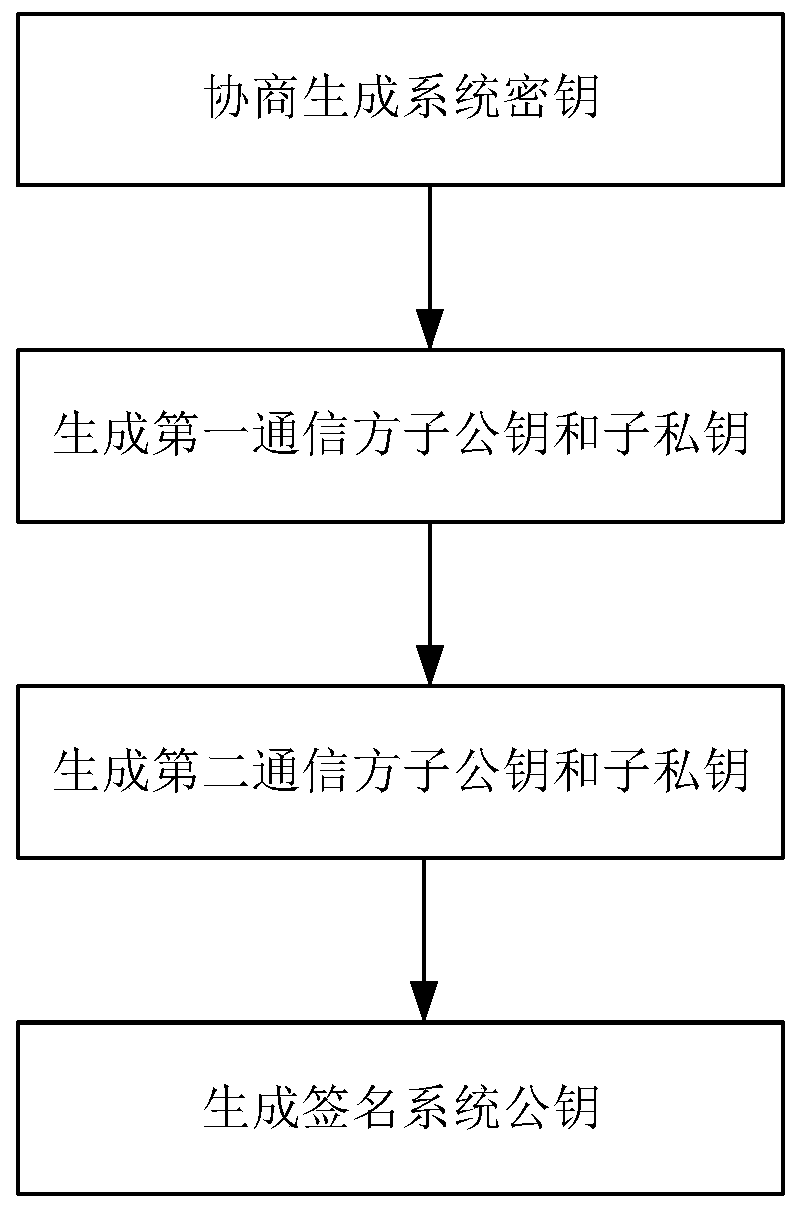
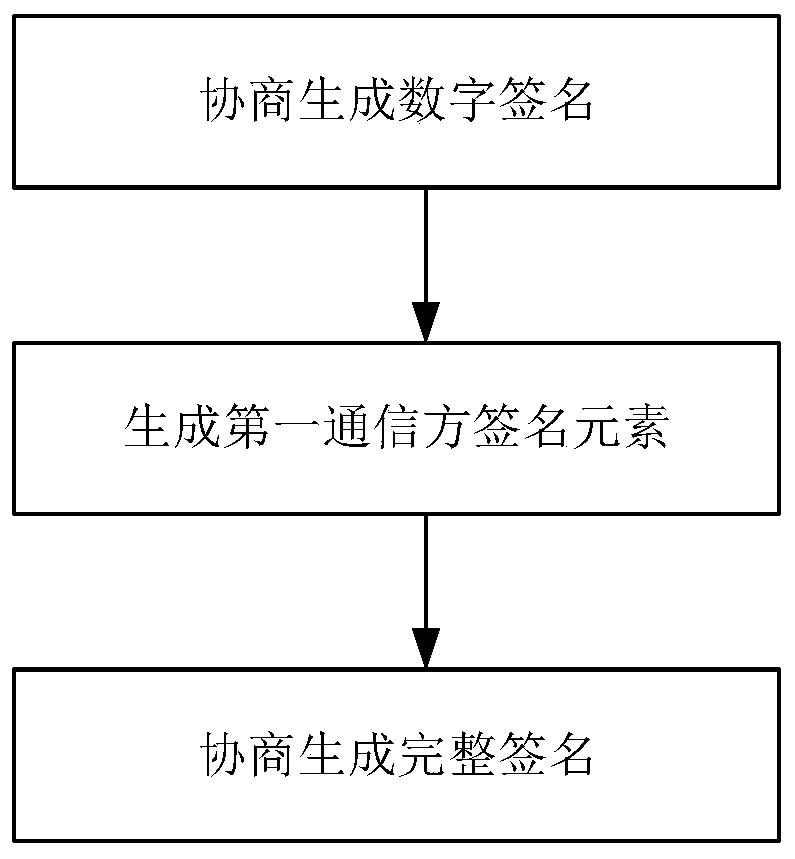
[0113] The steps of the generation method based on the Edwards curve digital signature of the present embodiment are as follows, see figure 1 , 2 , 3:
[0114] (1) Negotiate to generate a system key
[0115] 1) Generate the sub-public key and sub-private key of the first communication party
[0116] The first communication party chooses a 1 A random string of bytes is used as the private key string k of the first communication party 1 ,w 1is 32, use the cryptographic hash function Hash to obtain the hash value str of the private key string of the first communication party with formula (1) 1 :
[0117] str 1 =Hash(k 1 ) (1)
[0118] The first communication party uses formula (2) to obtain the first communication party's sub-private key sl 1 :
[0119]
[0120] Wherein the hash function Hash selects the national secret SM3 method, len is the bit length of the hash value output by the hash function SM3, the value of len is 256, and the value of l is 2; the first com...
Embodiment 2
[0196] The steps of the generation method based on the Edwards curve digital signature of the present embodiment are as follows:
[0197] (1) Negotiate to generate a system key
[0198] 1) Generate the sub-public key and sub-private key of the first communication party
[0199] The first communication party chooses a 1 A random string of bytes is used as the private key string k of the first communication party 1 ,w 1 is 48, use the cryptographic hash function Hash to obtain the hash value str of the private key string of the first communication party with formula (1) 1 :
[0200] str 1 =Hash(k 1 ) (1)
[0201] The first communication party uses formula (2) to obtain the first communication party's sub-private key sl 1 :
[0202]
[0203] Wherein the hash function Hash selects the SHA-512 method, the value of len is 512, and wherein l is 4; the first communication party uses formula (3) to obtain the first communication party identifier perix1:
[0204]
[0205...
Embodiment 3
[0223] The steps of the generation method based on the Edwards curve digital signature of the present embodiment are as follows:
[0224] (1) Negotiate to generate a system key
[0225] 1) Generate the sub-public key and sub-private key of the first communication party
[0226] The first communication party chooses a 1 A random string of bytes is used as the private key string k of the first communication party 1 ,w 1 is 64, use the cryptographic hash function Hash to obtain the hash value str of the private key string of the first communication party with formula (1) 1 :
[0227] str 1 =Hash(k 1 ) (1)
[0228] The first communication party uses formula (2) to obtain the first communication party's sub-private key sl 1 :
[0229]
[0230] Wherein the hash function Hash selects the SHA-256 method, the value of len is 256, and wherein l is 8; the first communication party uses formula (3) to obtain the first communication party identifier perix1:
[0231]
[0232...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com