LR triangular decomposition method based on symmetric sparse matrix technology and non-zero element random storage
What is Al technical title?
Al technical title is built by PatSnap Al team. It summarizes the technical point description of the patent document.
A sparse matrix, non-zero element technology, applied in the direction of design optimization/simulation, etc., can solve problems such as the influence of the calculation speed of the Z-array, the difficulty of the symmetry of the Z-array elements, and the increase of redundant calculation.
Pending Publication Date: 2020-02-21
NANCHANG UNIV
View PDF0 Cites 4 Cited by
Summary
Abstract
Description
Claims
Application Information
AI Technical Summary
This helps you quickly interpret patents by identifying the three key elements:
Problems solved by technology
Method used
Benefits of technology
Problems solved by technology
And since it seeks W k 、H k The array does not take advantage of the structural characteristics of the E array elements, which increases a large number of redundant calculations; also because it calculates the Z k The order of the array is Z 1 ~ Z n , get Z k The order of array...
Method used
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more
Image
Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
Click on the blue label to locate the original text in one second.
Reading with bidirectional positioning of images and text.
Smart Image
Examples
Experimental program
Comparison scheme
Effect test
Embodiment 1
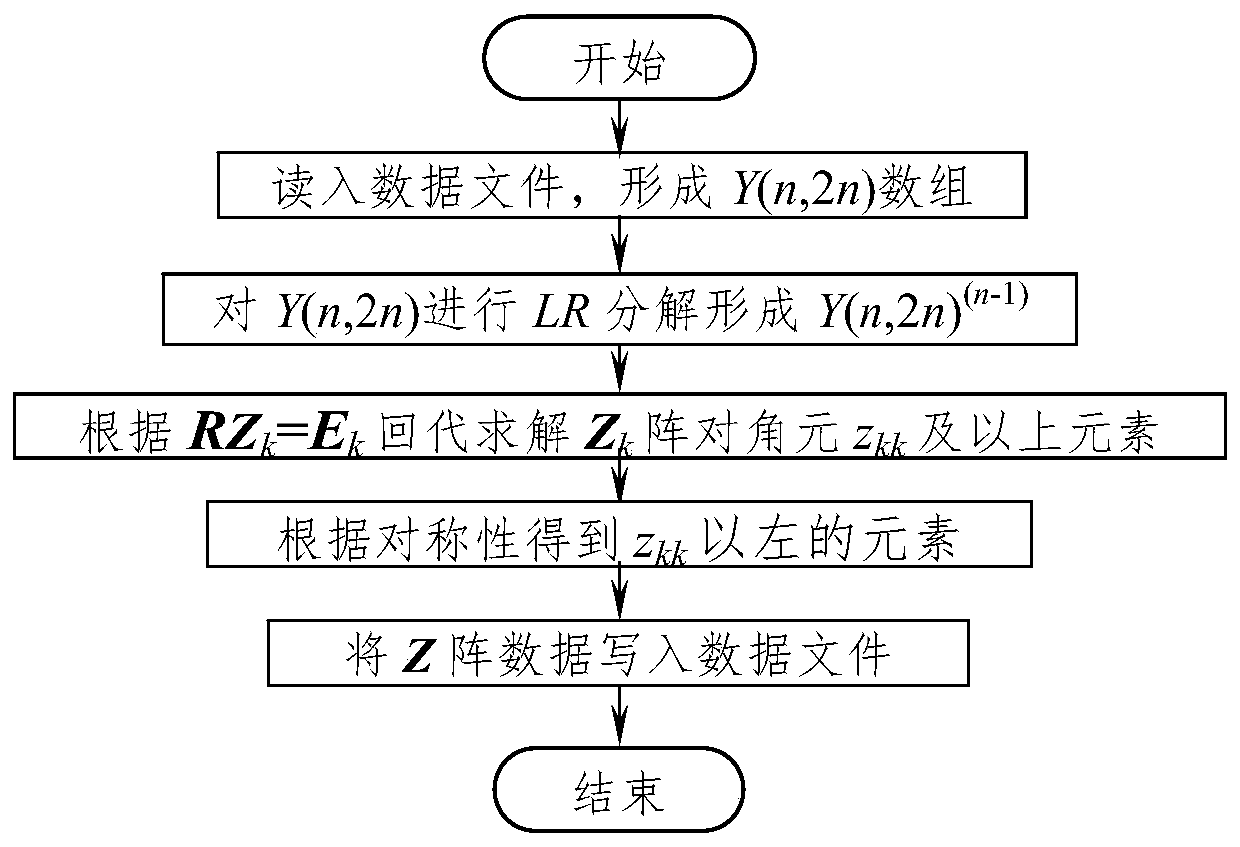
[0084] Example 1. In order to simplify the analysis, taking the fifth-order symmetric real number matrix as an example, the LR triangular decomposition is performed on the Y(n, n) and LR(n, d) arrays with only diagonal elements and upper triangular elements, and the calculation process is compared.
[0085] Note: Since the real number matrix is used, the Y(n, n) array is used here instead of the Y(n, 2n) array, and the second group in the LR(n, d) array has only 2 columns instead of 3 columns, and the third Each subgroup in the group has only 3 columns instead of 5.
[0086] (1) The initial state of the Y(n, n) and LR(n, d) arrays.
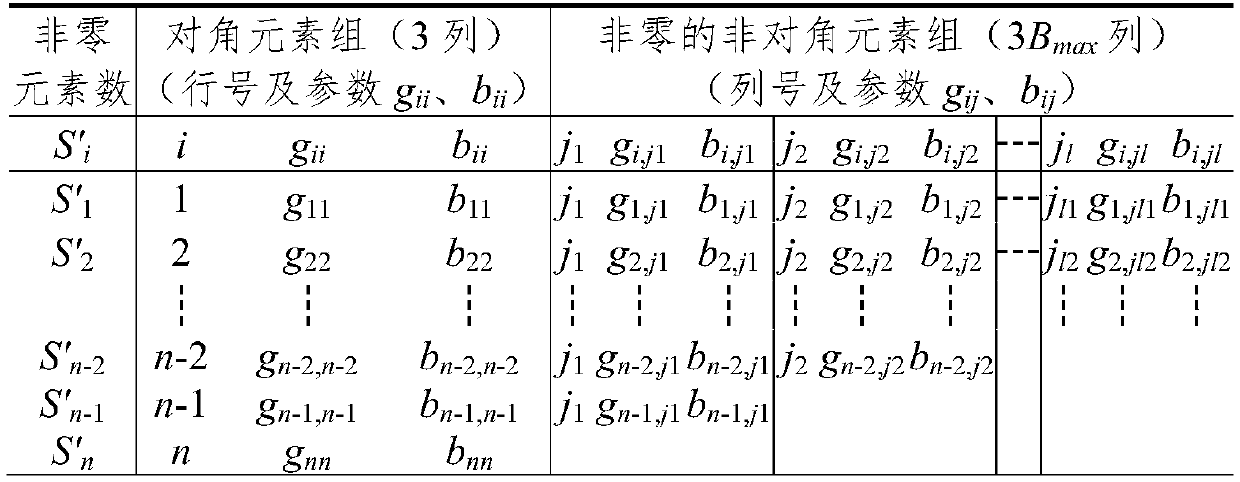
[0087] The Y(n, n) array elements are sequentially arranged symmetrically, while the LR(n, d) array elements are randomly asymmetrically arranged. The initial states of Y(n, n) and LR(n, d) arrays are shown in Table (1-1) and Formula (1-1). At this time, the first diagonal element in the LR(n, d) array and the non-zero elements to the right are...
Embodiment 2
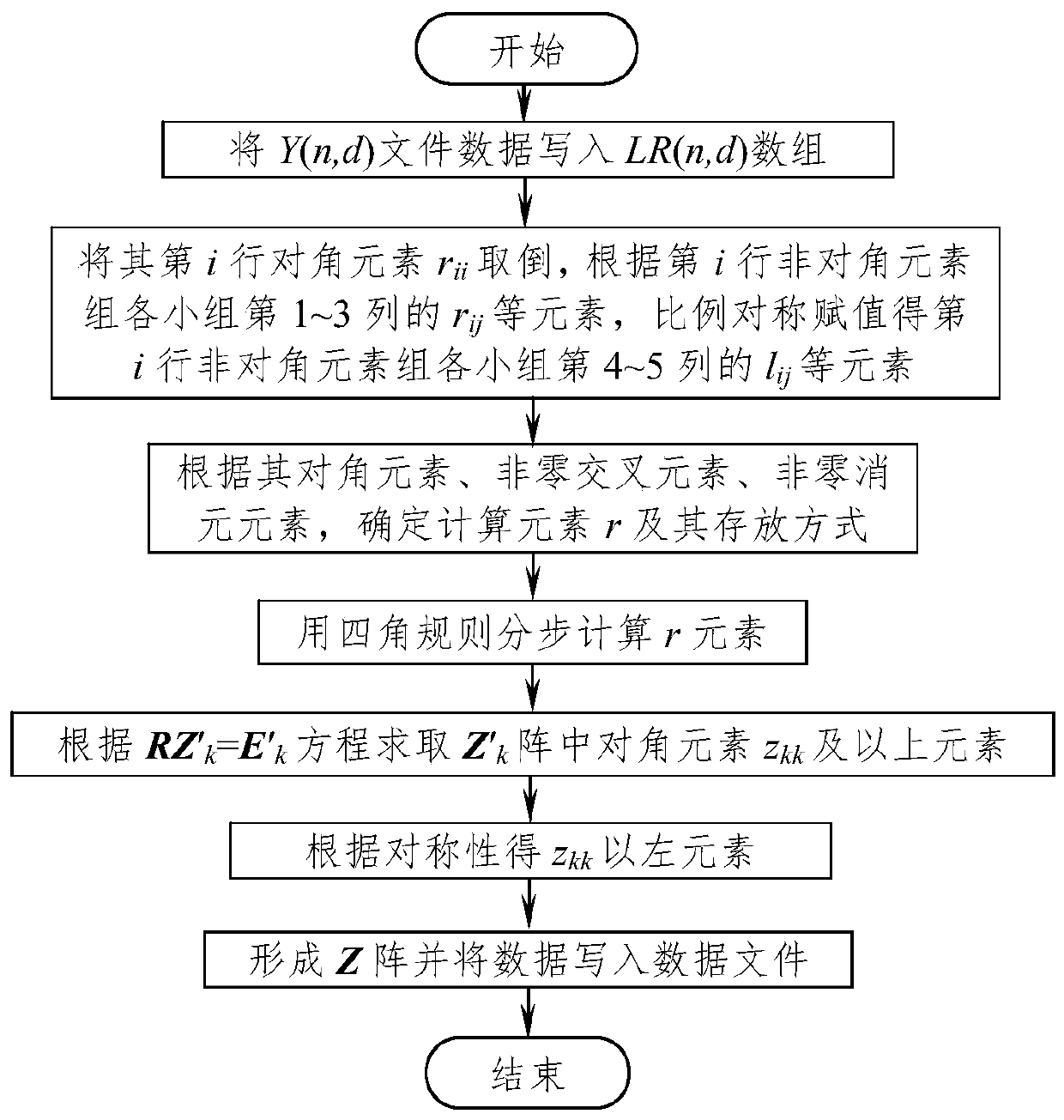
[0127] Example 2. For IEEE-30~-300 systems, the traditional LR decomposition method and this method are used to obtain the Z matrix respectively. The comparison results of the data file reading time, LR decomposition time, and LR decomposition + back-generation time are shown in Table 4.
[0128] Table 4 Comparison of calculation time between traditional method and this method for solving Z matrix
[0129]
[0130] Note: For the convenience of comparison, in this embodiment, the same method as this method is applied to the back-substitution process of the traditional LR decomposition method, that is, considering E k The characteristics of array element structure, Z k Array and Z k The order of obtaining the array elements, eliminating the need for the intermediate matrix W k To obtain, directly use RZ′ k =E' k Find Z' k Diagonal element z in the array kk and the above elements, and then get z according to the symmetry kk Take the left element.
[0131] t 1r : read...
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
PUM
Login to view more
Abstract
The invention provides an LR triangular decomposition method based on a symmetric sparse matrix technology and non-zero element random storage, and belongs to the field of power system analysis and calculation. The method mainly comprises the following steps: writing Y-matrix Y (n, d) data file data stored according to a random sequence into an LR (n, d) array; obtaining a reciprocal of the diagonal element rii in the ith row, and assigning elements such as lij in the fourth column to the fifth column in the ith row of non-diagonal element group at a time according to the column proportion according to the elements such as rij in the first column to the third column in the ith row of non-diagonal element group; determining a calculation element r and a storage mode thereof according to thediagonal element, the non-zero cross element and the non-zero elimination element; calculating an element r step by step by using a quadrangle rule; solving diagonal elements zkk and elements above zkk in the Z'k matrix according to an RZ'k = E'k equation; obtaining elements on the left of zkk according to symmetry; and writing the Z matrix data into a data file. For an IEEE-300 node system, compared with a traditional LR decomposition method, the method has the advantages that the data file reading time, the LR decomposition time and the LR decomposition + back substitution time are about 5.75%, 2.16% and 6.83% and are all reduced along with increase of the system scale.
Description
technical field [0001] The invention relates to analysis and calculation in the field of power system engineering, and mainly relates to an LR triangular decomposition method based on a symmetrical sparse matrix technology and random storage of non-zero elements, and is applied to obtain a node impedance matrix. Background technique [0002] There are mainly three triangular decomposition methods widely used in power system analysis and calculation, power flow calculation, active and reactive power optimization, etc. to solve constant coefficient equations, including LR, CU, and LDU. In practical applications, the LDU decomposition method is mostly used. However, in the calculation process, the number of elements involved in the calculation of l and r elements required by the LR decomposition method to form the factor matrix is relatively small, and only n intermediate matrices W need to be solved k . However, the LDU decomposition method needs to calculate the number of ...
Claims
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
Application Information
Patent Timeline
Application Date:The date an application was filed.
Publication Date:The date a patent or application was officially published.
First Publication Date:The earliest publication date of a patent with the same application number.
Issue Date:Publication date of the patent grant document.
PCT Entry Date:The Entry date of PCT National Phase.
Estimated Expiry Date:The statutory expiry date of a patent right according to the Patent Law, and it is the longest term of protection that the patent right can achieve without the termination of the patent right due to other reasons(Term extension factor has been taken into account ).
Invalid Date:Actual expiry date is based on effective date or publication date of legal transaction data of invalid patent.
Login to view more 
Login to view more