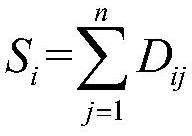A planning method for connecting two-dimensional random closed graphs to generate the shortest path
A shortest path and closed graphics technology, applied in program control, instrument, electrical program control, etc., can solve practical complex problems that are not practical enough, it is difficult to achieve global optimization, and the solution effect is not very ideal, etc., to shorten the processing time path, improved accuracy, highly optimized effects
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
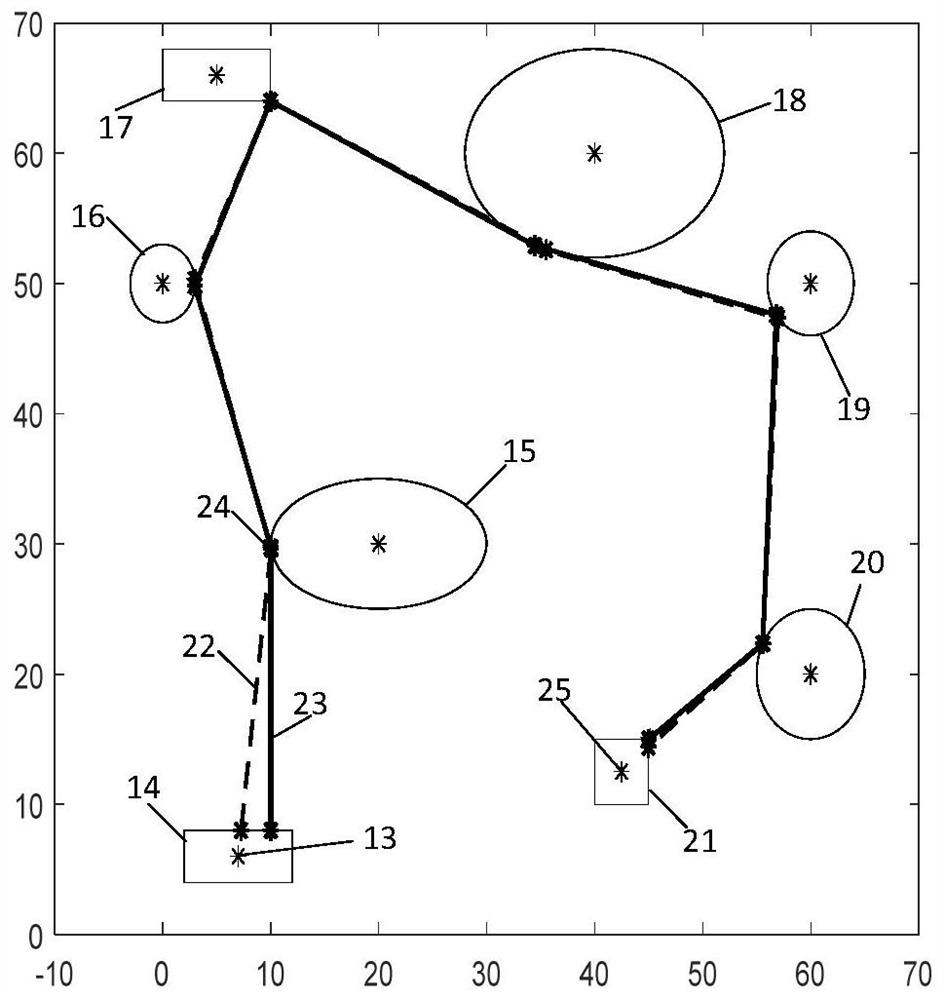
[0037] The present invention will be further described below in conjunction with the accompanying drawings and embodiments. Since two-dimensional point trajectory planning and two-dimensional closed graphics are not easy to be combined and represented, the two methods are shown separately in the attached drawing.
[0038] like figure 1 Shown: the present invention provides a kind of shortest path planning method that is applied to connecting two-dimensional plane data point, and this method is input with two-dimensional data point 1, and the open-loop shortest path L that obtains on two-dimensional plane 2 is output, and uses modified The greedy algorithm optimizes the total path. Parameters include path length L, point P i with P j the distance D between ij , point P i Total distance S to other points i , curve equation l.
[0039] The steps of two-dimensional data point path planning are as follows:
[0040] 1) Selection of starting point;
[0041] For the centroid ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com