Dynamic structure reliability evaluation method based on uncertain random variables
A technology of random variables and dynamic structures, applied in random CAD, special data processing applications, instruments, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
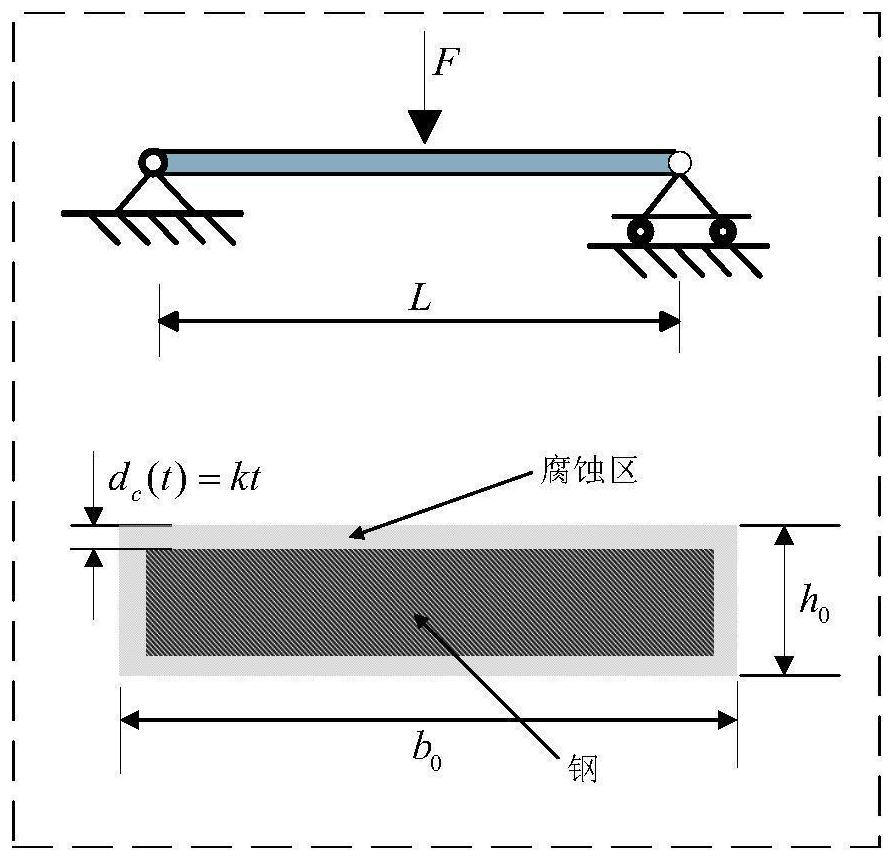
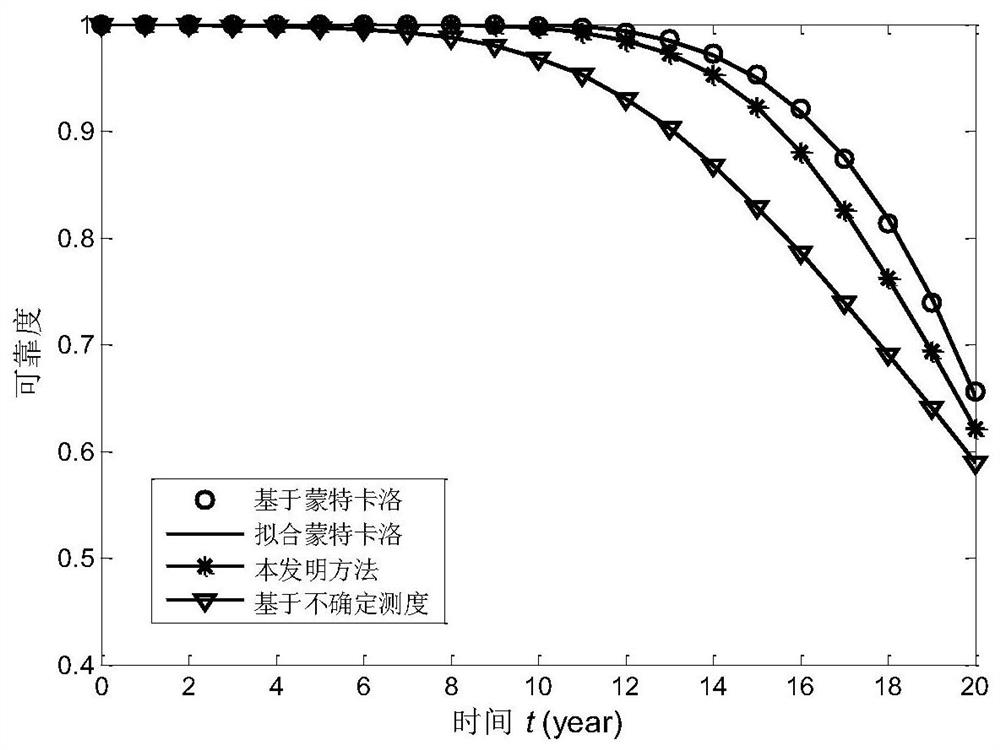
[0095] Under uniform load p = ρb 0 h 0 and a corroded bending beam of concentrated force F as figure 2 shown. The length of the curved beam is L=5m, and its section is rectangular, where b 0 =0.18m is the section width, h 0 =0.035m is the section height, ρ is the density of the curved beam. Assume the corrosion depth d of the corroded curved beam c has a functional relationship d with time t c =kt,k=2.5×10 -4 m / year, so the formulas for the length and width of the section of the beam are respectively b(t)=b 0 -2kt, h(t)=h 0 -2kt. When the maximum bending moment M of the bending beam is greater than the ultimate bending moment M u (t) is regarded as failure, and the expression of the limit state function is obtained as follows:
[0096]
[0097] In the formula, σ e is the yield stress, which obeys random normal distribution, while F and ρ obey uncertain linear distribution, namely: and σ e , F and ρ are independent of each other. Table 1 lists the specific di...
Embodiment 2
[0141] Such as Figure 5 In the four-bar truss structure shown, the elastic modulus and cross-sectional area of each bar are E=2.95×10 11 N / m 2 and A, both rods 1 and 2 have length L. Now exert a vertical downward (y-axis negative direction) time-varying force F on node 3 1 (t)=5(1+0.05t)×10 4 N, apply a time-varying force F horizontally to the right (positive direction of the x-axis) on node 2 2 (t)=5(1-0.05t)×10 4 N, where the unit of time t is hour. When the displacement of a node in the truss structure exceeds the limit threshold D max =0.328×10 -3 m is considered invalid. Assume that the rod length L obeys a random normal distribution, and the cross-sectional area A obeys an uncertain normal distribution, namely: And L and A are independent of each other. Table 4 lists the specific distribution parameters of random variables and uncertain variables.
[0142] The concrete distribution parameter of random variable and uncertain variable of table 4 embodiment 2 ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com