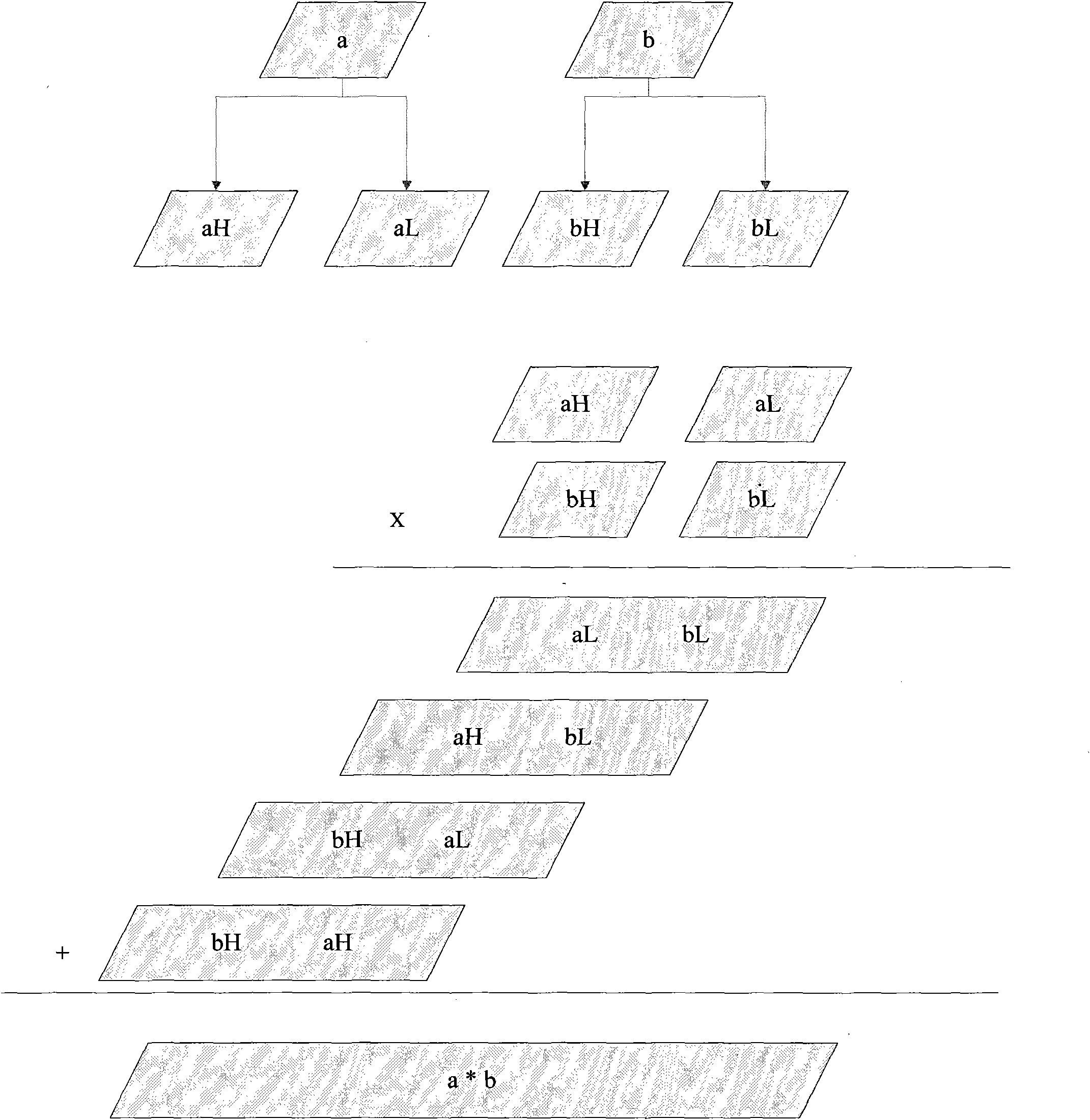Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

RSA (Ron Rivest, Adi Shamir and Leonard Adleman) algorithm digital signature method

A technology of RSA algorithm and digital signature, applied in key distribution, can solve the problem of low calculation efficiency of software modulo function, and achieve the effect of quick time to market and lower chip cost.

Active Publication Date: 2012-07-11
BEIJING CEC HUADA ELECTRONIC DESIGN CO LTD
View PDF3 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0013] In the modulo operation in step 1, due to the low calculation efficiency of the software modulo function, the hardware Montgomery modulo multiplication calculator is generally used to calculate

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • RSA (Ron Rivest, Adi Shamir and Leonard Adleman) algorithm digital signature method
  • RSA (Ron Rivest, Adi Shamir and Leonard Adleman) algorithm digital signature method
  • RSA (Ron Rivest, Adi Shamir and Leonard Adleman) algorithm digital signature method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0027] The invention can make the L / 2-bit long modular multiplier calculate the L-bit long RSA private key operation, so as to reduce the chip cost, or use limited resources to meet market changes, and help the rapid development and listing of products. This algorithm can be used when it is necessary to use a small bit length modular multiplier to realize a large bit length RSA private key operation. Specific steps are as follows:

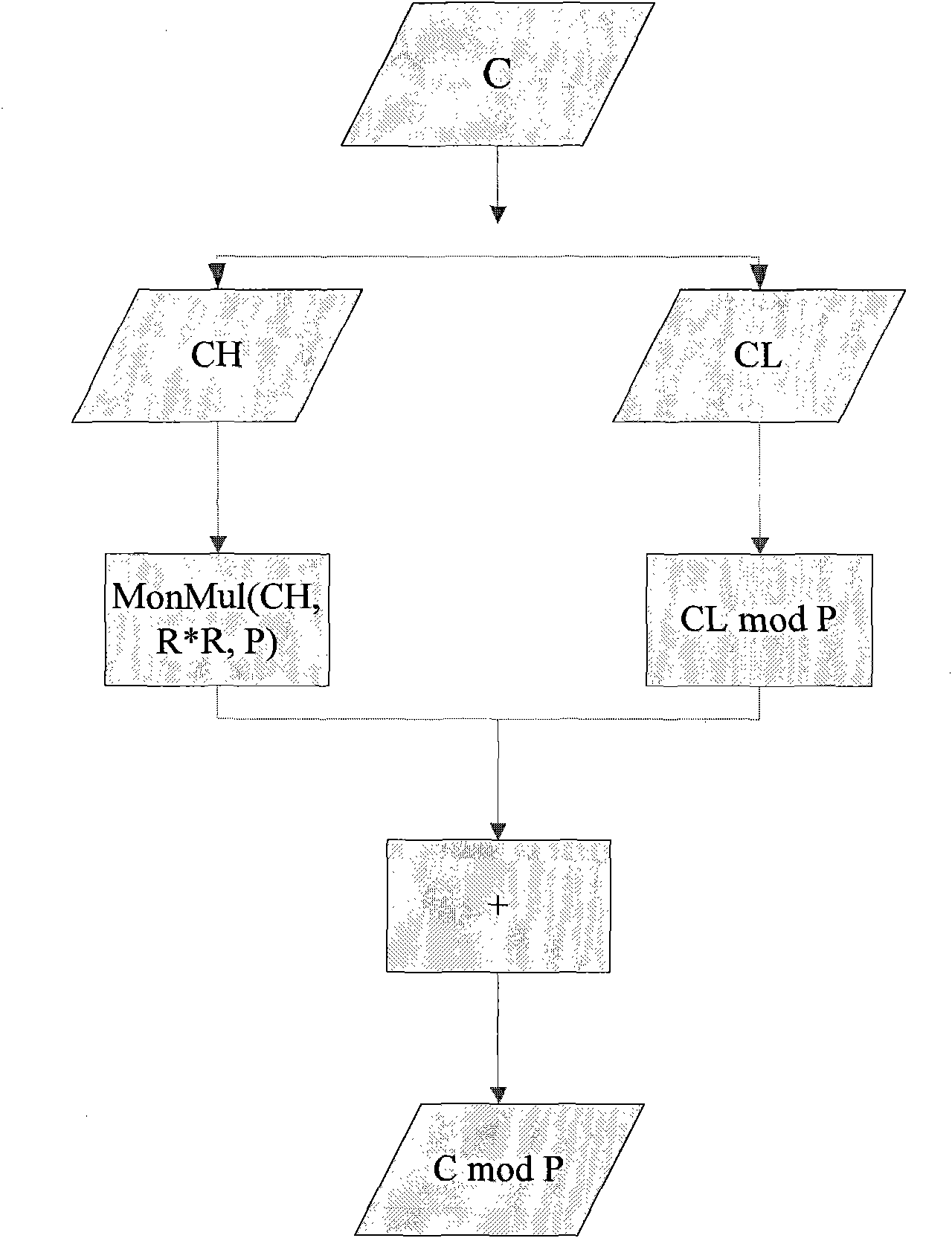
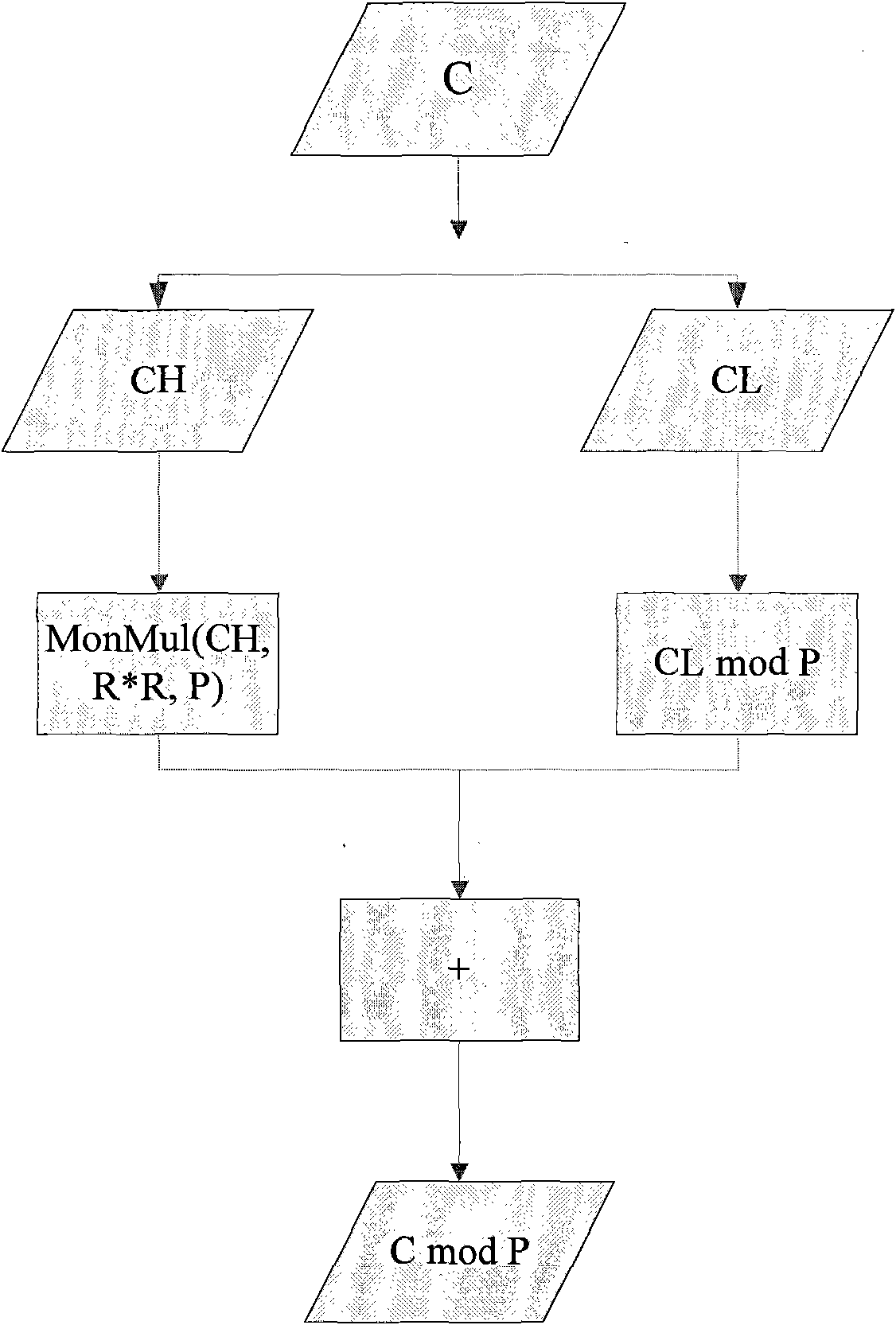
[0028] The following method is used when calculating C mod P:

[0029] 1. Divide C into two parts of equal length, record CH as the high L / 2 part, and CL as the low L / 2 part, so that the L-length C is split into two L / 2-length data, and C=CH<<L / 2+CL, where "<<" is a leftward translation operation.

[0030] 2. Further analysis of CH<

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention designs an RSA (Ron Rivest, Adi Shamir and Leonard Adleman) algorithm digital signature method which realizes a 1408-bit RSA private key operation technology based on a 1024-bit hardware coprocessor and is mainly applied to the field of safety calculation of smart cards. A parameter in a large-bit-length RSA private key operation is calculated by utilizing a modular multiplier with small bit length, for example, a parameter in 1408-bit or 2048-bit RSA private key operation is calculated by utilizing a modular multiplier of 1024 bits. The RSA private key operation utilizes a Chinese remainder theorem and can be used for reducing the operation length of a main operation-modular exponentiation, but an operation of a key parameter, such as C mod P, C mod Q and a multiply operation, wherein the C represents a plain text, the length of the C is double the lengths of the P and the Q; and the multiply operation is accelerated by utilizing the modular multiplier, and a final result is also over the calculation capability of the modular multiplier. In the technology of the invention, the C is split into two numbers with the small bit lengths to calculate the C mod P by mainly utilizing the algorithm deformation of modular arithmetic; and the multiply operation larger than the length of the modular multiplier is calculated through a quarter multiply operation.

Description

Technical field: [0001] The invention is mainly applied in the field of smart card security calculation. Background technique: [0002] RSA private key operation mainly involves two key technologies: [0003] 1. Use the Montgomery modular multiplication algorithm: [0004] Note the Montgomery modular multiplication as MonMul(a, b, m), then: [0005] MonMul(a, b, m) = a*b*R -1 mod m, where the bit length of a, b, m is L, R=2 L , R -1 Meet R -1 *R modm=1, mod is modulo operation. [0006] 2. Use the Chinese remainder theorem for acceleration: [0007] Note that the input data of the RSA private key operation is C, and the RSA private key parameters are p, q, d and n, where the bit length of p and q is L / 2, and the bit length of d and n is L, then the RSA private key The operation Cd mod n can be transformed into a modular exponentiation operation on p and q through the definition of Chinese remainder to improve the running speed. The following is a brief description o...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/32H04L9/08
Inventor 汪涛范楠迪马宁
Owner BEIJING CEC HUADA ELECTRONIC DESIGN CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com