Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

In-depth extracting method of three-viewpoint stereoscopic video restrained by time-space domain

A technology for stereoscopic video and depth extraction, applied in stereoscopic systems, image data processing, instruments, etc.

Active Publication Date: 2014-04-02
SHANGHAI JIAO TONG UNIV
View PDF4 Cites 28 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Therefore, the method is limited to depth estimation of stationary scenes and requires sufficient motion of the camera

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • In-depth extracting method of three-viewpoint stereoscopic video restrained by time-space domain
  • In-depth extracting method of three-viewpoint stereoscopic video restrained by time-space domain
  • In-depth extracting method of three-viewpoint stereoscopic video restrained by time-space domain

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0115] The present invention will be described in detail below in conjunction with specific embodiments. The following examples will help those skilled in the art to further understand the present invention, but do not limit the present invention in any form. It should be noted that those skilled in the art can make several modifications and improvements without departing from the concept of the present invention. These all belong to the protection scope of the present invention.

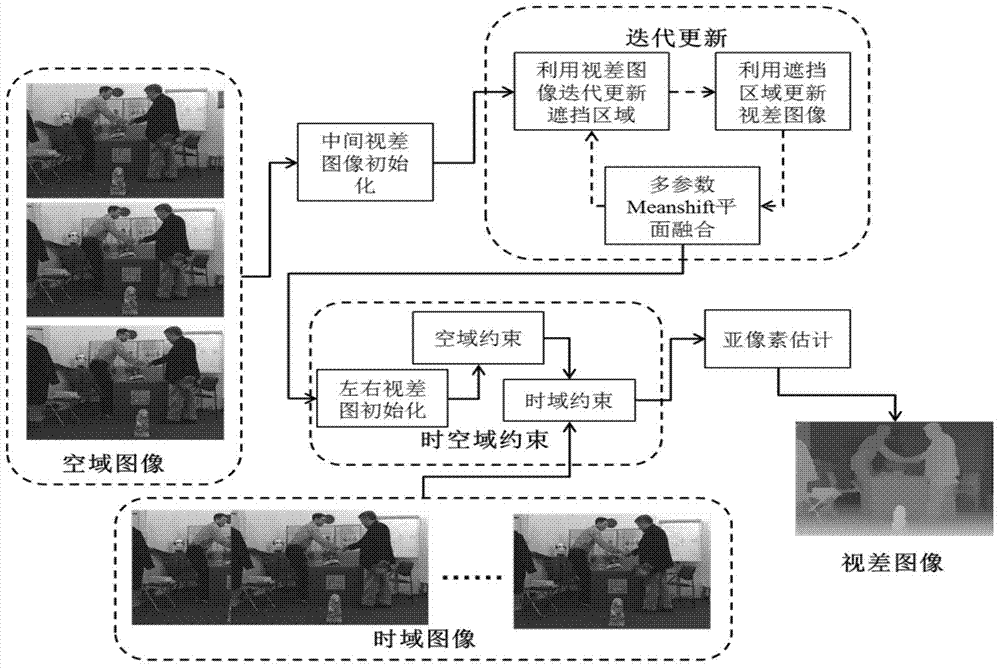
[0116] Such as figure 1 As shown, the three-viewpoint depth sequence estimation method of the present invention includes the initialization of the disparity map of the middle viewpoint, iterative update of the disparity map and the occlusion image, the initialization of the left and right disparity images, the space-time constraints and the sub-pixel estimation.

[0117] The first step, for the intermediate viewpoint image I t,L , to obtain its initial matching energy distribution, use the BP al...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an in-depth extracting method of a three-viewpoint stereoscopic video restrained by time-space domain. The method comprises the steps of searching an optimal matching point from left and right viewpoint images by aiming at a center viewpoint image, optimizing a parallax error estimation process based on an energy function by adopting a BP algorithm and a plane fusion method, adopting three-view parallax error and shielding information iterative optimization, establishing a time domain parallax error constraint relation between adjacent frames through an optical flow method, defining the confidence coefficient of the optical flow method, so as to restrain parallax error sequence time domain hopping, eliminating errors caused by parallax error value quantification by utilizing binomial sub pixel estimation and bilateral filters, obtaining the parallax error of sub pixel accuracy, quantizing the obtained parallax error, and then obtaining a final in-depth sequence. Compared with the prior art in which constraint is performed by adopting a single frame only, the method has the advantages that the method searches multi-reference frame optical flow, and can better avoid the propagation of space domain error on time domain, thereby being capable of obtaining a continuous and accurate in-depth image sequence on time-space domain through a three-viewpoint image.

Description

technical field [0001] The present invention relates to a method in the technical field of depth extraction of stereoscopic video, in particular to a method for extracting depth information of three-viewpoint stereoscopic video by utilizing joint constraints of time and space domains. Background technique [0002] Because the depth image contains the three-dimensional structure information of the scene, it is widely used in 3D modeling (3D Modeling), image layer segmentation (Layer Separation), depth image based rendering (Depth Image Based Rendering) and video editing in the field of computer vision. (Video Editing), etc. For stereoscopic images, the disparity information of stereoscopic images can be obtained by applying techniques such as corresponding point matching, and the corresponding depth information of stereoscopic images can be obtained by quantifying the extracted disparity. Therefore, depth information extraction, as an important foundation and basic topic of ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04N13/00G06T7/00
Inventor 周军徐抗孙军冯可
Owner SHANGHAI JIAO TONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com