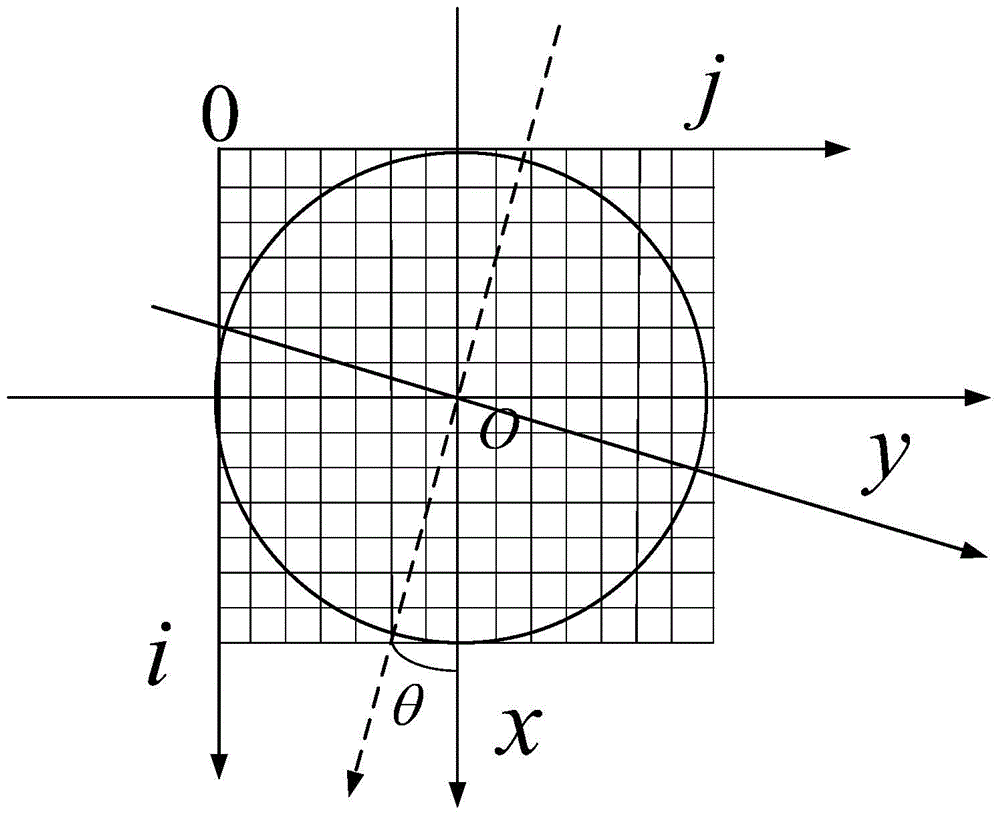Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Discrete Radon projection and Mojette projection conversion method based on fixed resolution

A conversion method and resolution technology, applied in the field of computed tomography, which can solve the problems of long reconstruction time, high radiation dose, and the inability of the projection model to apply to discrete images.

Active Publication Date: 2015-09-09
DALIAN UNIV OF TECH
View PDF2 Cites 22 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] However, since the imaging system is a digital discrete system, the continuous projection model cannot be applied to discrete images, so the discrete Radon transform randomly emerges
The discrete Radon transform and its inverse transform solve the problem of converting from the analog domain to the digital domain, but the reconstruction algorithm based on the inverse Radon transform requires a large number of sampling samples and projections to reconstruct a better reconstructed fault. It will lead to too high radiation dose and too long reconstruction time. Considering that the patient's health and the dynamic changes of lesions in medical imaging will cause artifacts, it is necessary to perform high-quality imaging in a short time, low dose and sparse angle. important, yet challenging

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Discrete Radon projection and Mojette projection conversion method based on fixed resolution
  • Discrete Radon projection and Mojette projection conversion method based on fixed resolution
  • Discrete Radon projection and Mojette projection conversion method based on fixed resolution

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach

[0112] S1 sets the projection parameters, under the projection vector (1,2), project a 3×3 small block, and set the number of detector pixels B=10>(3-1)|1|+(3- 1)|2|+1=7;

[0113] When the S2 projection vector is (1,2), the corresponding projection angle θ=tan -1 1 / 2 = 26.5651°;

[0114] S3 establishes the corresponding 0-order B-spline interpolation projection system System_rad under the projection vector (1,2) 26.6 , set DetCCDSize=0.4mm here.

[0115] S3.1 Traversing each pixel point, clarifying which projection rays pass through each pixel point, and calculating the effective range of these projection rays hitting the detector.

[0116] It is assumed that the actual physical size of the reconstruction pixel is ObjPixel, ObjPixel=1mm; the actual physical size of the detector pixel is DetCCDSize, DetCCDSize=0.4mm.

[0117] Traverse each pixel {Pixel(i,j)|i,j∈Z,1<i<3,1<j<3}, and calculate the effective range of the ray passing through each pixel on the detector , accordi...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A discrete Radon projection and Mojette projection conversion method based on a fixed resolution is disclosed, which belongs to the technical field of computer imaging in the field of image processing. The discrete Radon projection and Mojette projection conversion method is characterized by converting a sparse angle discrete Radon projection under an actual imaging condition into a Mojette projection which is accurately reconstructed in a discrete domain. Based on the computer tomography imaging algorithm, Radon and Mojette projection scenes are simulated by constructing a reasonable imaging system; and after the relation between the Mojette projection and the Radon projection is analyzed in detail, a specific algorithm of converting the Radon projection into the Mojette projection under a corresponding projection vector at each projection angle on the premise of a given fixed resolution. The discrete Radon projection and Mojette projection conversion method has the effects and the benefits that at different sparse projection angles, the resolution of an Radon projection image does not need to be changed; the conversion disorder between variation of the resolution of a Mojette projection domain along with the projection vector and the constant resolution of the Radon projection is overcome; and a conversion bridge between the two projections is set up.

Description

technical field [0001] The invention belongs to the technical field of computer tomography (CT) in the field of image processing, and relates to the problem of sparse sampling and high-efficiency restoration in the image projection transformation domain. Background technique [0002] CT technology is a computer-based three-dimensional reconstruction technology that can reproduce the invisible internal slice structure of an object without damaging the surface and internal structure of the object. In terms of CT imaging algorithms, according to the different imaging principles, it is divided into analytical and iterative reconstruction algorithms; according to the reconstruction accuracy, it is divided into approximate reconstruction and precise reconstruction algorithms. In the analytical algorithm, the transformation model proposed by the Austrian mathematician Radon uses low-dimensional compressed projection data to reconstruct the high-dimensional object structure. This ma...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06T3/20
CPCG06T3/20G06T2207/10072
Inventor 孙怡李梦婕蒋敏
Owner DALIAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com