Method for numerical solution of fuzzy steady state heat conduction problem based on full grid point collocation theory
A technology of numerical solution and heat conduction, applied in the field of mechanical engineering, it can solve the problems of difficult mathematical expression, inability to meet the refined analysis and design of complex heat transfer systems, and inconvenience.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0054] The present invention will be further described below in conjunction with the accompanying drawings and embodiments.
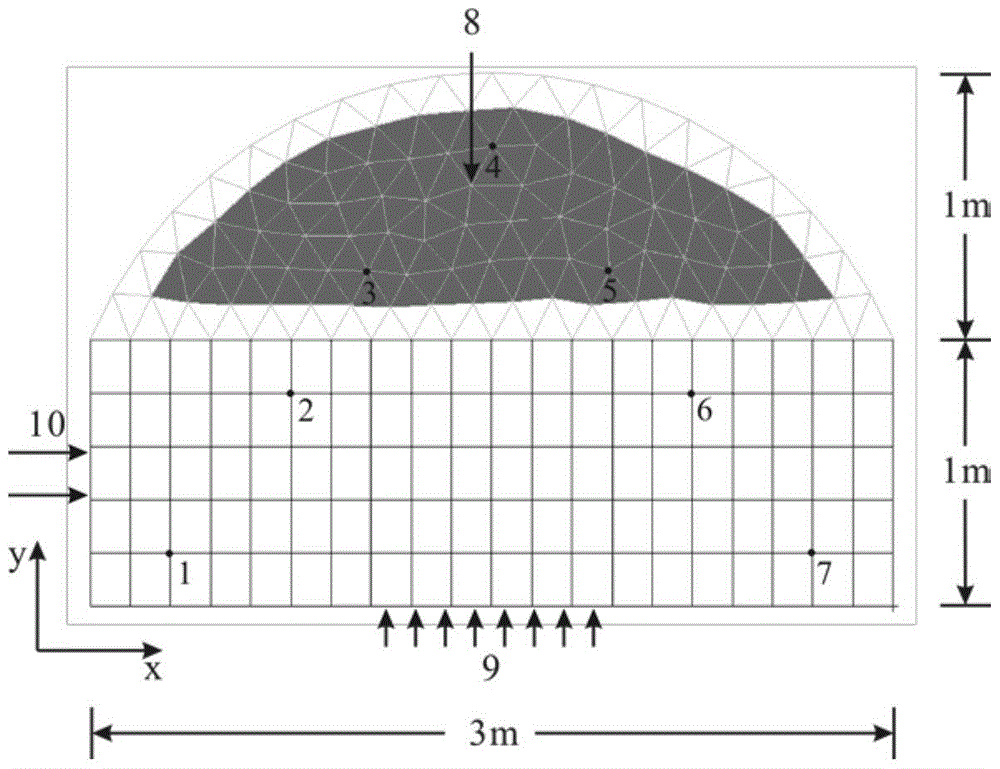
[0055] The invention is suitable for predicting the structural temperature field of the steady-state heat conduction problem containing fuzzy uncertain parameters. In this embodiment, the temperature field prediction of a flat heat transfer structure is taken as an example to specifically illustrate the numerical solution method for the fuzzy steady-state heat conduction problem. In addition, the numerical calculation method of the fuzzy and uncertain temperature response of the plate heat transfer structure can be extended to other steady-state heat transfer problems with fuzzy parameters to predict the temperature field.
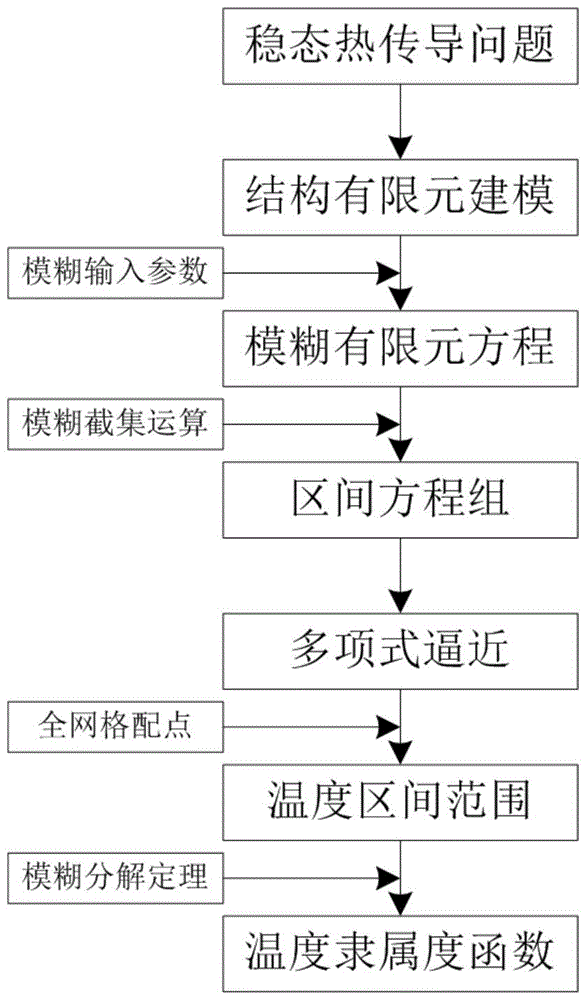
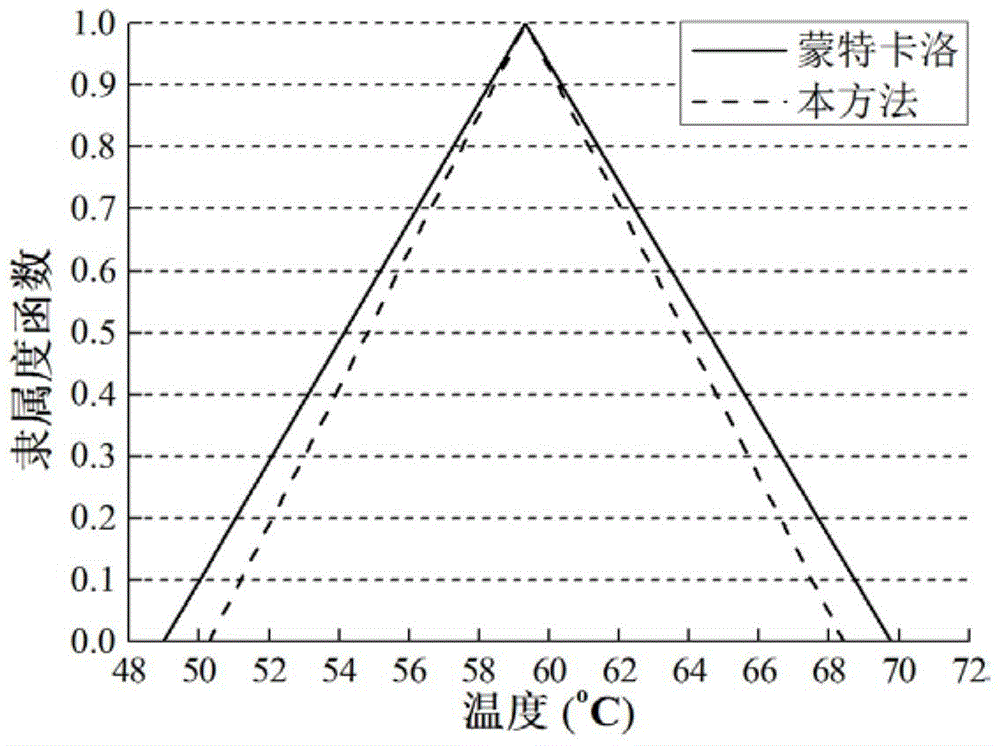
[0056] The numerical calculation process of the fuzzy steady-state heat conduction problem is as follows: figure 1 As shown, based on the finite element model of the structure, the discrete equation of the heat transfer system is e...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com