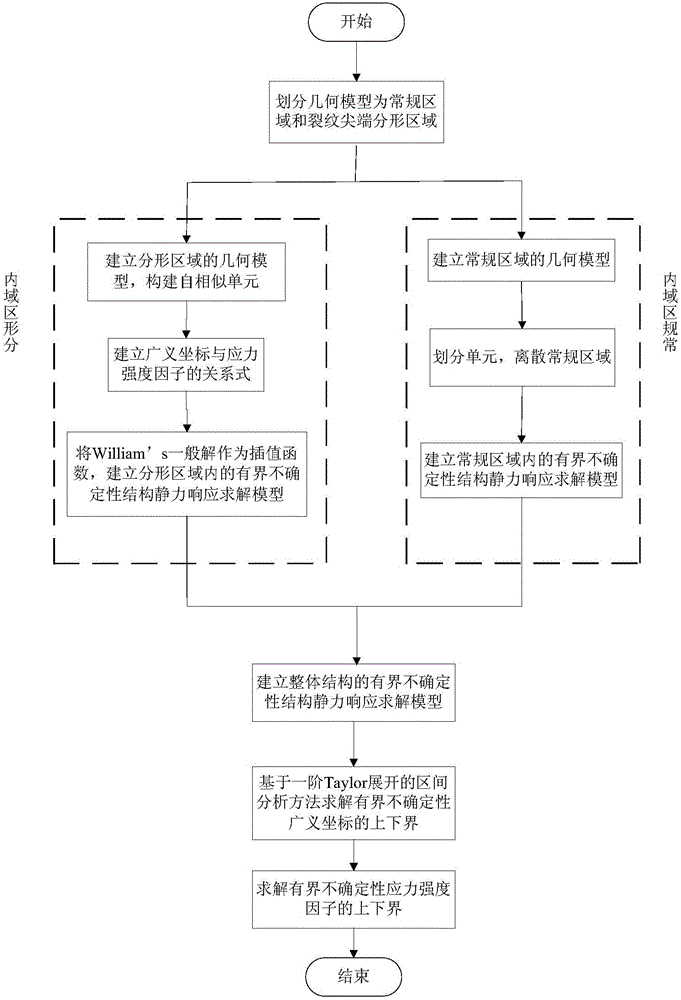
Method for predicting upper and lower bounds of bounded uncertain plane crack stress intensity factors based on fractal theory

A stress intensity factor and uncertainty technology, applied in special data processing applications, electrical digital data processing, instruments, etc., can solve problems such as limiting the actual progress of engineering, failing to meet engineering needs, and ignoring the dependence of probability methods

Active Publication Date: 2016-07-27
BEIHANG UNIV
View PDF4 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The above work enriches the analysis of plane crack stress intensity factors to a certain extent, but ignores the dependence of the probability method on the sample information, which greatly limits the progress of its theory in engineering practice
Due to poor information and lit...

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for predicting upper and lower bounds of bounded uncertain plane crack stress intensity factors based on fractal theory
  • Method for predicting upper and lower bounds of bounded uncertain plane crack stress intensity factors based on fractal theory
  • Method for predicting upper and lower bounds of bounded uncertain plane crack stress intensity factors based on fractal theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

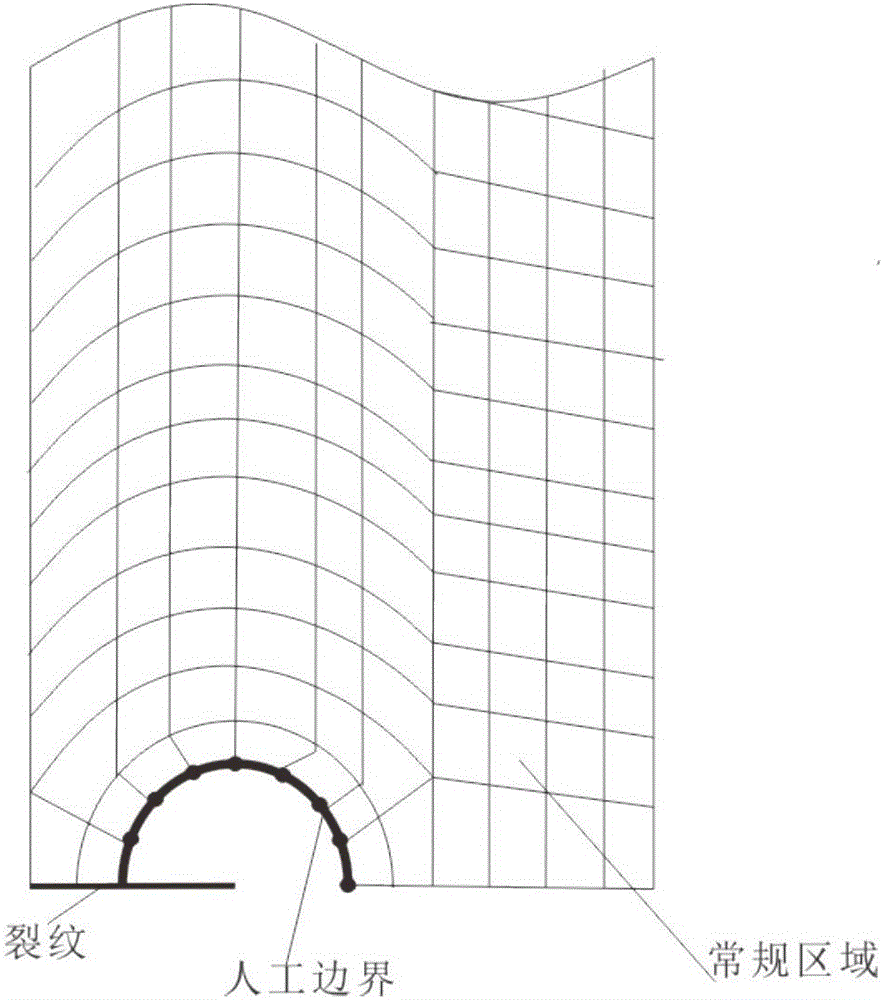
[0160] In order to understand more fully the characteristics of the invention and its applicability to engineering practice, the present invention aims at such as image 3 ( image 3 Modified) for an elastic plate with a unilateral crack for bounded uncertainty stress intensity factor boundary evaluation. image 3 The width of the medium elastic plate is w=400mm, the height is h=2000mm, the crack length is a, and the modulus of elasticity is E=2×10 5 MPa, Poisson's ratio ν = 0.167, under the action of the uniform Brass force F. Due to manufacturing and measurement errors, both the crack length a and the uniform force F are bounded uncertainty parameters, and the central value of the crack length a is a C =50mm, the central value of uniform pull force F is F C =300MPa, and a=[50-1.5β,50+1.5β], F=[300-9β,300+9β], β is a variable coefficient of variation, respectively 0.05,0.10,0.15,0.20,0.25 . In this example it is necessary to predict the bounds of the stress intensity fac...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a method for predicting upper and lower bounds of bounded uncertain plane crack stress intensity factors based on a fractal theory. According to a geometric model including a crack structure, the geometric model is divided into a conventional region and a fractal region of crack tips by using an artificial boundary to establish a bounded uncertain structural static force response solution model in the conventional region; a William's general solution is used as an interpolation function to establish a bounded uncertain structural static force response solution model in the fractal region; then, assembly is performed to obtain a whole bounded uncertain structural static force response solution model including a crack structure, the upper and lower bounds of bounded uncertain generalized coordinates are calculated by adopting a first-order Taylor expansion based interval analysis method, and further the upper and lower bounds of the bounded uncertain plane crack stress intensity factors are calculated. The upper and lower bounds of the bounded uncertain plane crack stress intensity factors are calculated are accurately and efficiently obtained by adopting the method, and objective and effective data is provided for reliability evaluation and design of structures.

Description

technical field [0001] The invention is applicable to the prediction of the upper and lower bounds of the stress intensity factor of a bounded uncertainty plane crack, and specifically relates to a prediction method of the upper and lower bounds of the stress intensity factor of a bounded uncertainty plane crack based on fractal theory and a non-probability interval analysis method. Background technique [0002] In engineering practice, mechanical equipment and metal structure components often have macroscopic cracks caused by manufacturing, use or defects of the material itself. At this time, to determine whether the component can continue to be used safely, the most important thing is to judge whether the crack will expand unstable and cause damage to the structure and equipment. The stress intensity factor reflects the stress field and displacement field near the crack tip, and is a measure of the crack growth tendency and crack growth driving force. From the point of vi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/50
CPCG06F30/20
Inventor 邱志平孙佳丽王晓军王磊吕峥王冲陈潇王鹏博
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap