Supercharge Your Innovation With Domain-Expert AI Agents!

UUV (Unmanned Underwater Vehicle) path tracking method based on self-adaption sliding-mode control

An adaptive sliding mode and path tracking technology, applied in adaptive control, general control system, control/regulation system, etc., can solve the problems of complex construction and slow implementation, achieve high control accuracy, reduce chattering, Small chattering effect

Active Publication Date: 2017-01-04
HARBIN ENG UNIV
View PDF4 Cites 45 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, this method is complex to construct, slow to implement, and has many limitations.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • UUV (Unmanned Underwater Vehicle) path tracking method based on self-adaption sliding-mode control
  • UUV (Unmanned Underwater Vehicle) path tracking method based on self-adaption sliding-mode control
  • UUV (Unmanned Underwater Vehicle) path tracking method based on self-adaption sliding-mode control

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0035] Specific implementation mode one: combine Figure 4 , the UUV path tracking method based on adaptive sliding mode of the present invention, comprises the steps:

[0036] Step 1. Initialization:

[0037] is various adaptive parameters k of UUV i ,λ i (i=1,2,3) assign initial value, and determine its ideal speed u for the path following process d , define update times t=0;

[0038] Step 2. Obtain the current state of the UUV:

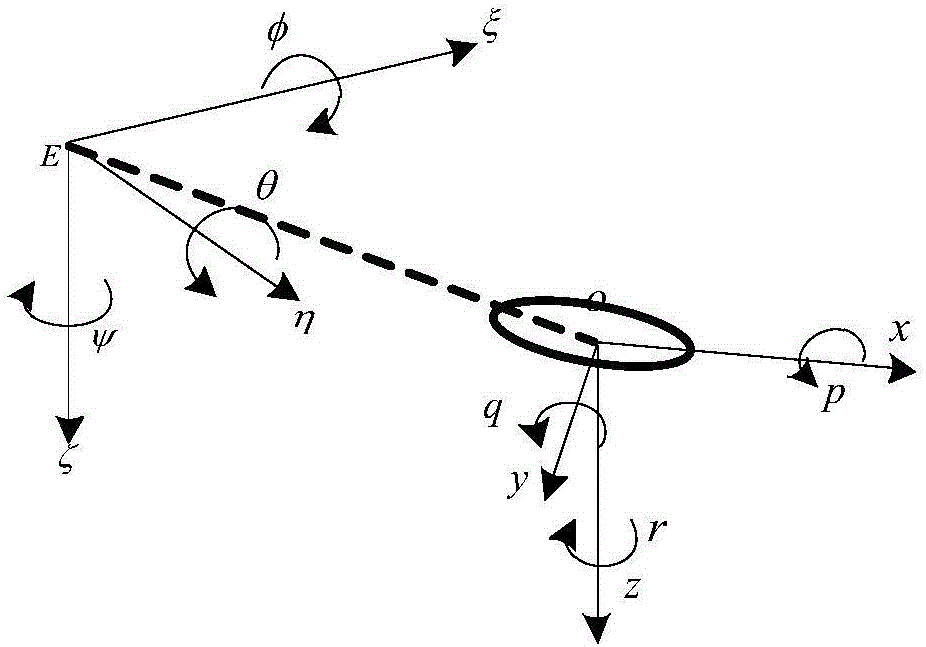
[0039] The current moment status is obtained through a series of sensors of the UUV itself: u, v are the longitudinal and lateral speeds (m / s), r are the yaw angular speeds (rad / s), and x, y are the UUV relative to the fixed coordinates position of the system (m), ψ is the yaw angle (rad), determine the longitudinal velocity error e u =u-u d ;

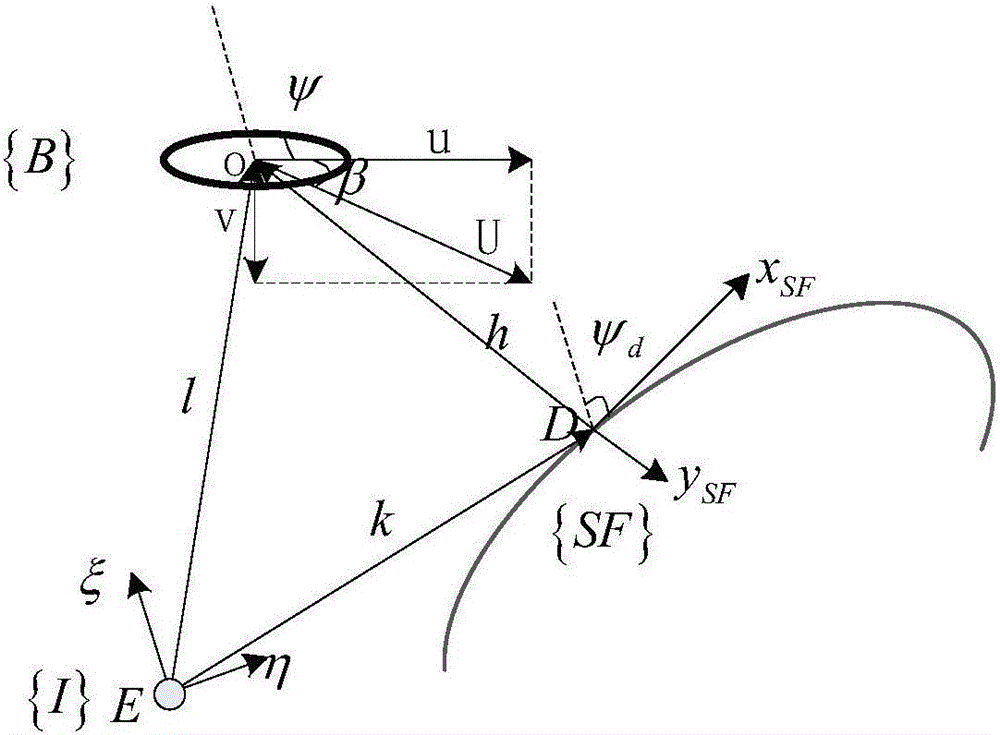
[0040] Step 3. Based on the Serret-Frenet coordinate system, establish the underactuated UUV horizontal plane error equation to obtain the position deviation x e ,y e and heading deviation ψ e ; ...

specific Embodiment approach 2

[0054] Embodiment 2: On the basis of Embodiment 1, based on the Serret-Frenet coordinate system described in step 3, the underactuated UUV horizontal plane error equation is established to obtain the position deviation x e ,y e and heading deviation ψ e The specific process is as follows:

[0055] For the movement of UUV in the horizontal plane, it is only necessary to establish a three-degree-of-freedom model, and the variables to be considered are: position x, y, heading angle ψ, longitudinal velocity u, lateral velocity v, and yaw angular velocity r. The kinematic equation of UUV horizontal plane can be obtained as:

[0056] x · = u c o s ψ - v s ...

specific Embodiment approach 3

[0089] Specific implementation mode three: on the basis of specific implementation mode one or two, utilize the sliding mode control method described in step 4 to design respectively the speed sliding mode control law, the position sliding mode control law and the bow angle sliding mode control law, by against thrust X prop , expected speed and torque N prop control so that u d →0,x e →0,ψ e →0 The specific process is as follows:

[0090] In order to design a controller designed for UUV path tracking, the present invention makes the following reasonable assumptions:

[0091] Assumption 1: The speed U of the UUV can be regarded as the longitudinal speed u of the UUV;

[0092] Hypothesis 2: Minimum speed u min and the maximum speed u max , so that u d ∈[u min , u max ],u max > u min >0;

[0093] On the basis of the above assumptions, the sliding mode control law of the UUV's speed tracking subsystem is firstly designed. For the first formula in (6), use

[009...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a UUV (Unmanned Underwater Vehicle) path tracking method based on self-adaption sliding-mode control. The method comprises the steps of 1, initializing; 2, obtaining a current state of a UUV; 3, establishing an underactuated UUV horizontal error equation to obtain the positional deviation xe, ye and a course deviation value psi e; 4, utilizing a sliding-mode control method to respectively design a speed sliding-mode control law, a position sliding-mode control law and a stem phase angle sliding-mode control law and enabling th ud to be zero, the xe to be zero and the psi e to be zero by controlling thrust Xprop, expected speed (shown in the following image) and torque Nprop; 5, updating a self-adaption law of handover gain and a self-adaption law of boundary layer thickness; 6, performing control input saturation compensation; 7, enabling k = k +1, returning to the step 2 and updating the control laws and the self-adaption laws for the next time to achieve the accurate control on the UUV horizontal path tracking. The UUV path tracking method can only depend on a controller which is designed according to a horizontal dynamical model to stabilize the system and is suitable for various underactuated UUVs.

Description

technical field [0001] The present invention relates to a UUV path tracking method, in particular to a tracking control method for an underdriven UUV in a horizontal plane to a desired path. Background technique [0002] The path tracking control of Unmanned Underwater Vehicle (UUV) is an important technical basis for realizing various uses of UUV. In-depth study of the problems existing in UUV path tracking is of great significance to UUV control theory and engineering applications. [0003] At present, in the aspect of underactuated UUV path tracking control, one of the more mainstream ideas is to establish a kinematic error equation based on the Serret-Frenet coordinate system, and then combine the error equation, dynamic equation and various control methods to achieve control. Among them, common control algorithms include backstepping, model predictive control, sliding mode variable structure control, etc. The backstepping method has obvious advantages in stabilizing c...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 张伟魏世琳孙希勋严浙平周佳加
Owner HARBIN ENG UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com