Method of continuum structure non-probabilistic reliability topological optimization under mixed constraints of displacements and stresses
A stress constraint and hybrid constraint technology, applied in design optimization/simulation, special data processing applications, instruments, etc., can solve problems such as large safety redundancy, loss, waste of resources, time cost, etc., to improve performance and reduce structural weight , the effect of reducing the design cycle and economic cost
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
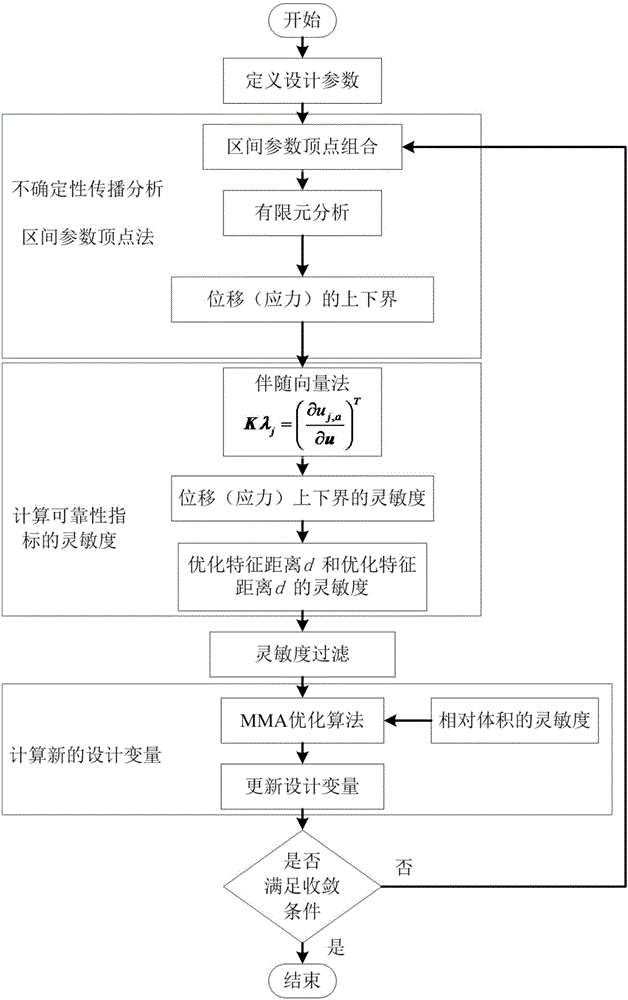
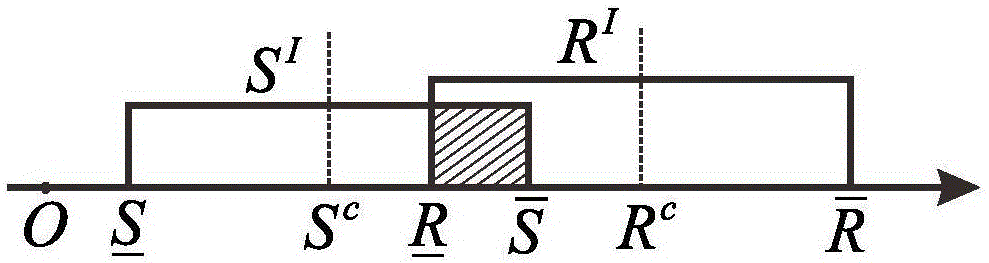
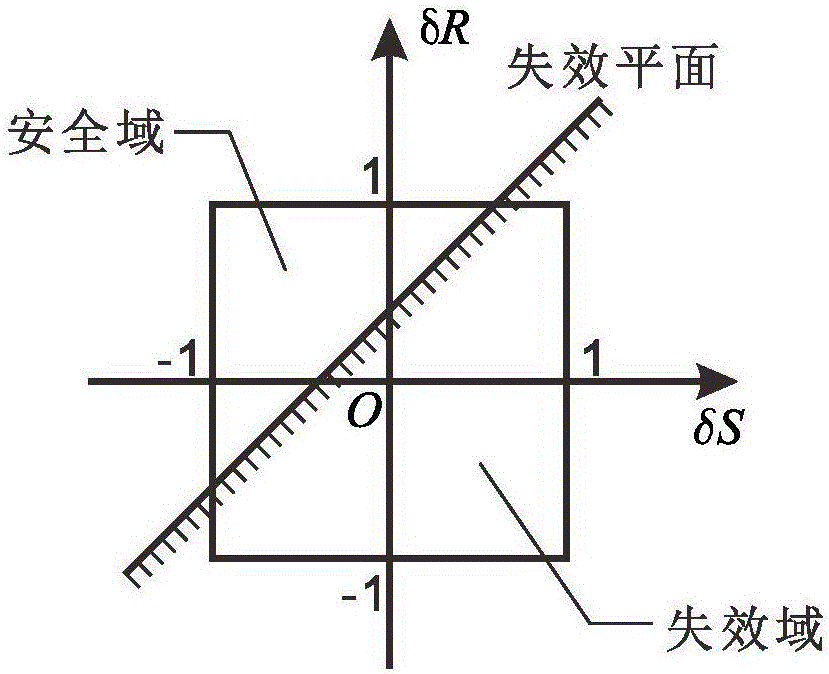
[0135] In order to understand more fully the characteristics of the invention and its applicability to engineering practice, the present invention aims at such as Figure 5 The shown rectangular area is designed for topology optimization. Among them, the size of the rectangular domain is 25mm×20mm, the thickness is 0.25mm, and it is divided into 100×80 units. The material is steel, the modulus of elasticity E=205Gpa, Poisson's ratio μ=0.3. The left end of the rectangular area is fixed, and a force of F=20N is added to point A at the bottom of the right end, regardless of the influence of gravity, and the displacement and stress of point A are constrained so that u A A A and the stress constraint σ A The fluctuation of the relative nominal value is: E=[189,231]Gpa, F=[18,22]N, u A =[0.5,0.6]mm, σ A =[400,500]Mpa. The relative density of the initial material is 1, and the structure is topologically optimized.
[0136] This example gives the results of topology optimization...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com